Integrated Math 1 Similarity and Congruence Worksheets
What Do Students Learn About Similarity and Congruence in Integrated Math 1?
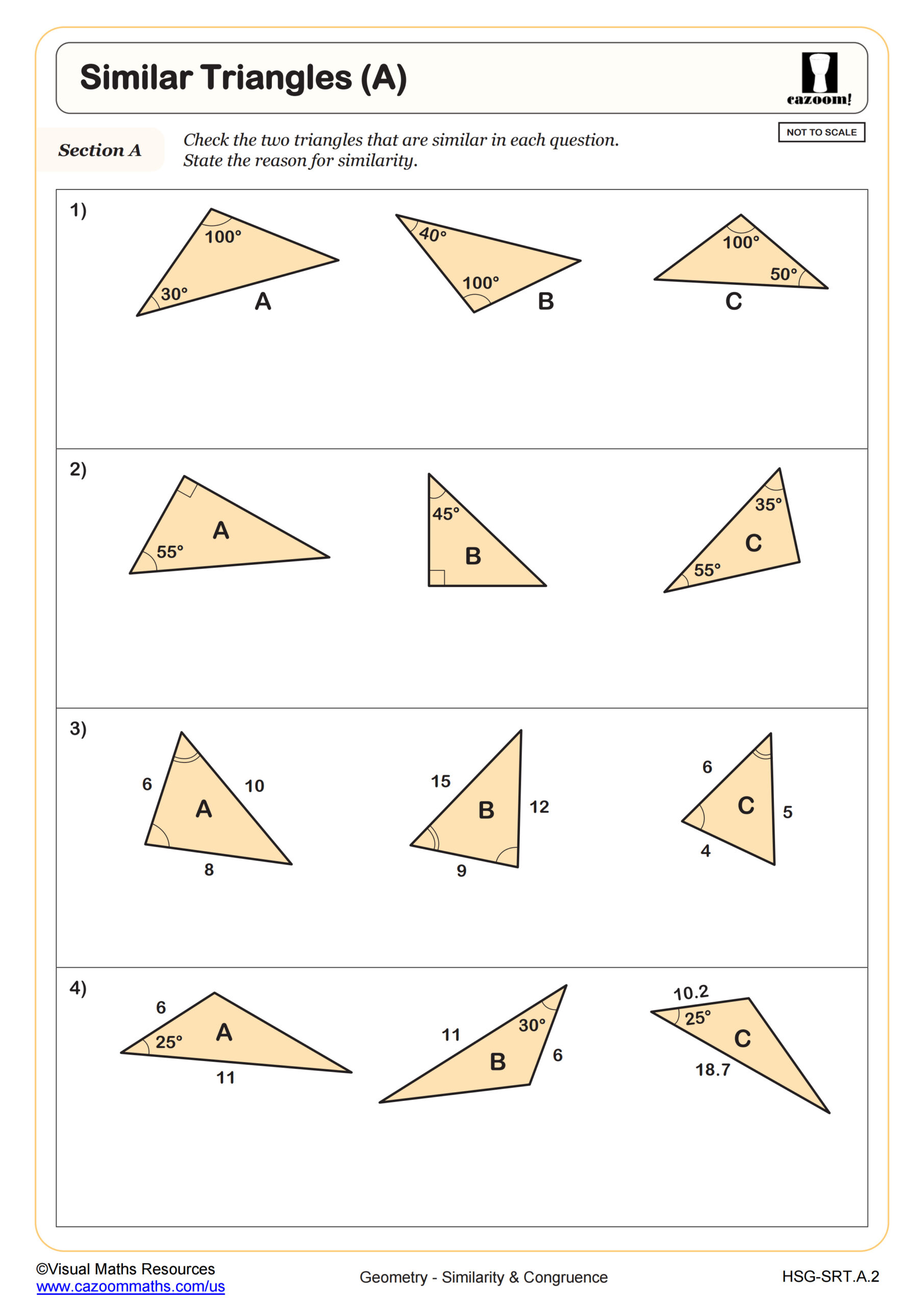
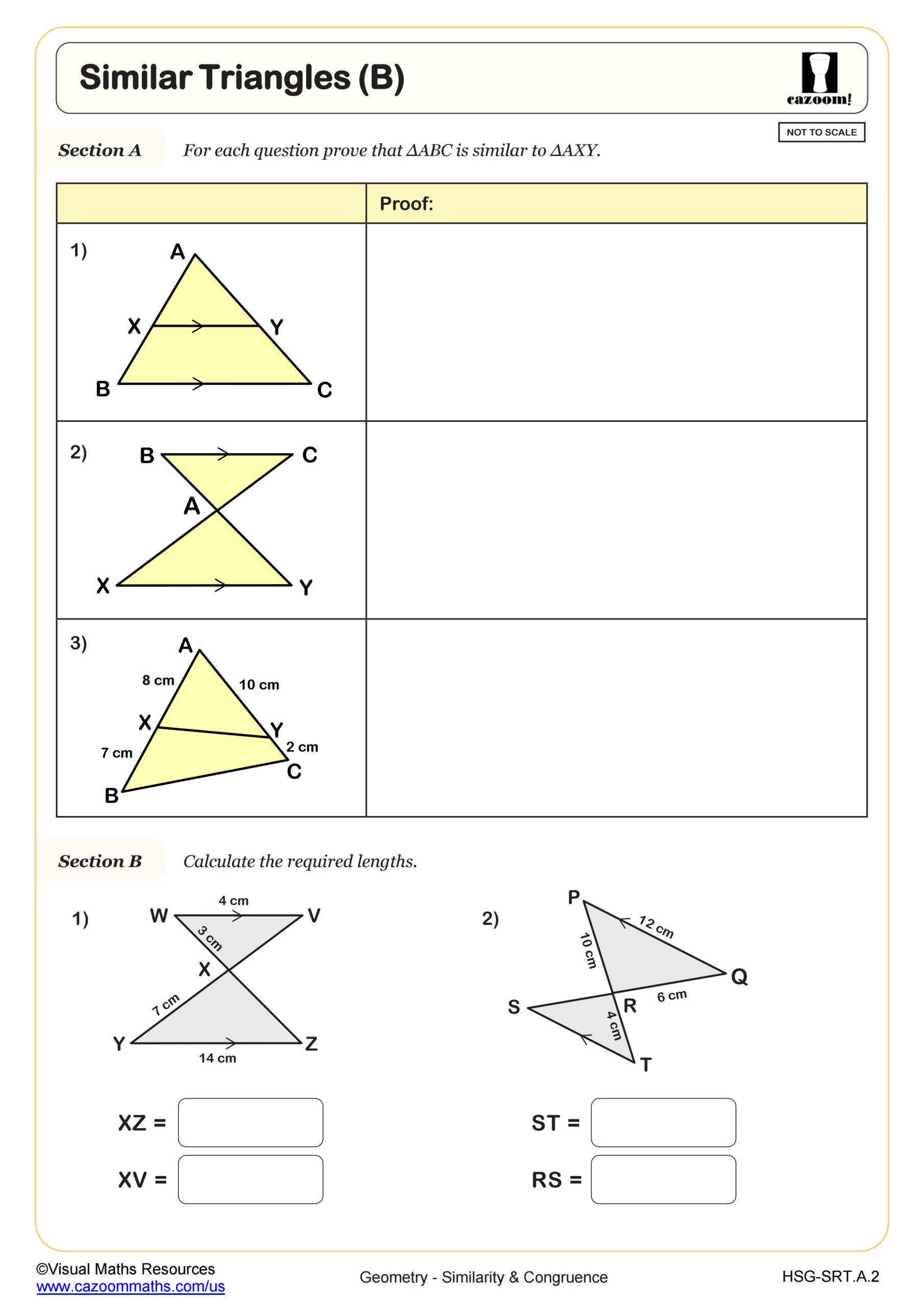
Integrated Math 1 introduces similarity and congruence through the lens of transformations, aligning with Common Core standards that emphasize geometric reasoning. Students learn that congruent figures result from rigid motions (translations, rotations, reflections) that preserve distances and angles, while similar figures result from dilations combined with rigid motions. They practice identifying congruence criteria for triangles, calculating scale factors, finding missing side lengths using proportional relationships, and proving triangle similarity through AA, SAS, and SSS theorems.
A common misconception surfaces when students assume all corresponding sides must be equal for similarity, confusing it with congruence. Teachers frequently observe students writing correct similarity statements but then setting up proportions with sides from different triangles or mixing corresponding parts. The breakthrough typically happens when students physically measure dilated figures and recognize that while side lengths change by a constant factor, angle measures remain unchanged.
How Do Similarity and Congruence Appear on Standardized Tests?
Standardized tests like the SAT and state assessments regularly include similarity and congruence problems that require students to justify geometric relationships rather than simply perform calculations. Questions often present two triangles with marked angles or sides and ask students to determine whether enough information exists to prove congruence or similarity. Students must demonstrate understanding of which congruence postulates apply (SSS, SAS, ASA, AAS) and recognize when SSA fails. The SAT particularly favors multi-step problems where students identify similar triangles within complex figures, then use proportional reasoning to find unknown measurements.
Students lose points when they assume triangles are congruent based on appearance rather than mathematical proof, or when they incorrectly apply SSA thinking it guarantees congruence. Another frequent error occurs when students correctly identify similar triangles but set up proportions with sides out of order, placing corresponding sides in different positions within the ratio. Test preparation should emphasize careful labeling of corresponding vertices and systematic checking of angle-side-angle relationships.
How Do Students Apply Scale Factors When Working With Similar Figures?
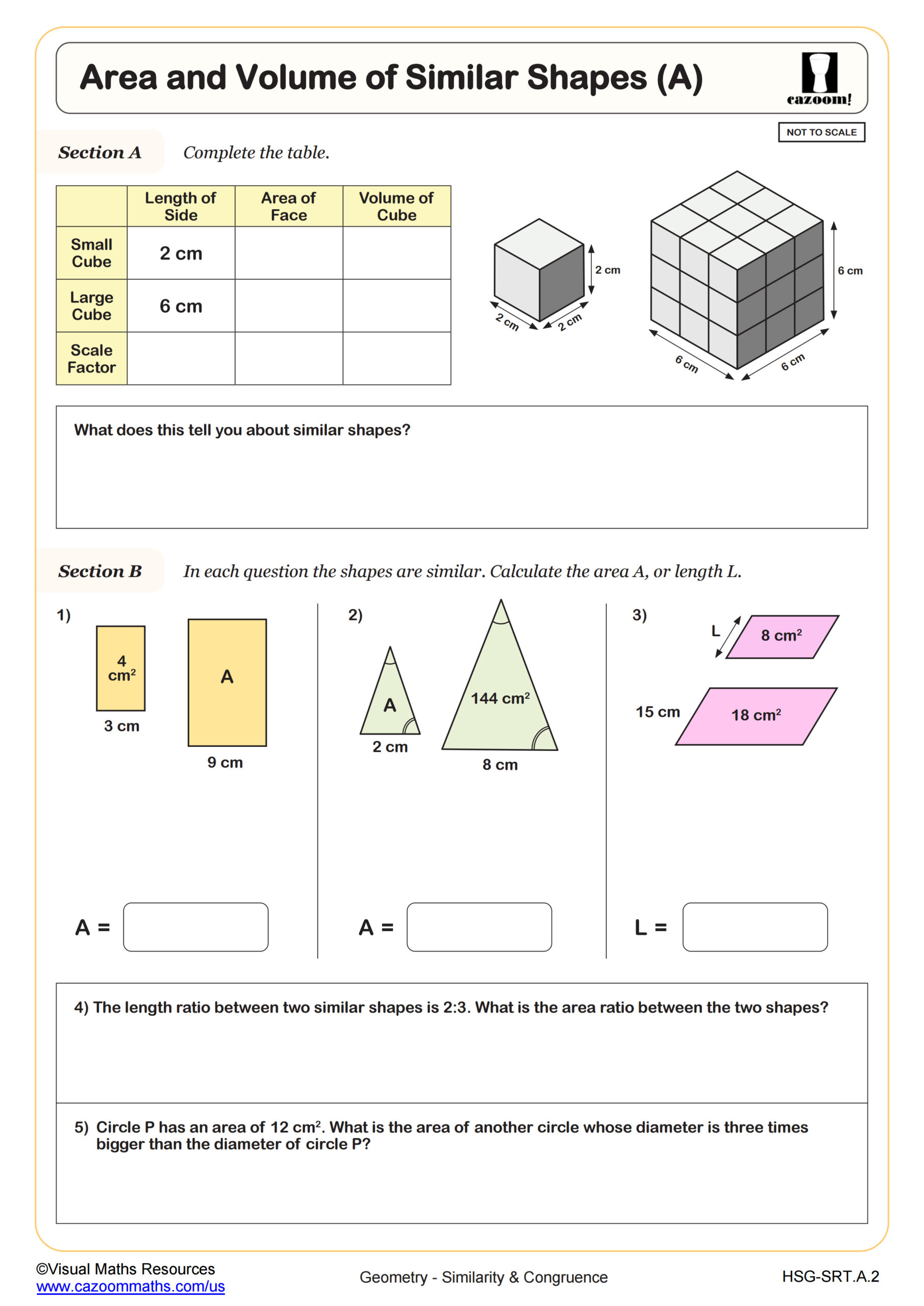
Scale factors quantify the multiplicative relationship between corresponding side lengths in similar figures. Students calculate scale factors by dividing a side length in the image by the corresponding side length in the pre-image, then apply that constant ratio to find unknown dimensions. When the scale factor exceeds 1, the image enlarges; when it falls between 0 and 1, the image reduces. Students also learn that while linear dimensions change by the scale factor, area changes by the square of the scale factor and volume by the cube of it.
Architects and engineers rely on scale factors daily when creating blueprints, scale models, and technical drawings. A landscape architect designing a park creates plans at a scale of 1:200, meaning every centimeter on the drawing represents 200 centimeters in reality. Urban planners use similar triangles formed by shadows to determine building heights without direct measurement. Students recognize the practical value when they calculate how changing dimensions affects material costs in construction projects or how digital images resize while maintaining proportions.
How Can Teachers Use These Similarity and Congruence Worksheets in Integrated Math 1?
These worksheets provide structured practice that builds from identifying congruent parts to constructing formal proofs and solving application problems. The problems progress systematically, allowing students to first master recognizing corresponding parts in diagrams before moving to multi-step reasoning about why figures must be congruent or similar. Answer keys enable students to self-check their work during independent practice, helping them identify exactly where their reasoning breaks down. Teachers find that having solutions readily available makes the worksheets equally valuable for whole-class instruction, small group work, or individual remediation.
Many teachers assign these worksheets as targeted practice before unit assessments or state tests, using them to identify which congruence postulates students confuse most often. The worksheets work well for stations during geometry review days, paired with hands-on activities using patty paper for transformations. Teachers also use selected problems as warm-ups to maintain skills throughout the year, since similarity and congruence concepts reappear in trigonometry, coordinate geometry, and proof-writing units. The consistent format helps students focus on mathematical reasoning rather than deciphering unfamiliar problem structures.