Integrated Math 1 Simplification Worksheets
Add and Subtract in Standard Form

Factoring Quadratic Expressions

Factoring Trinomials

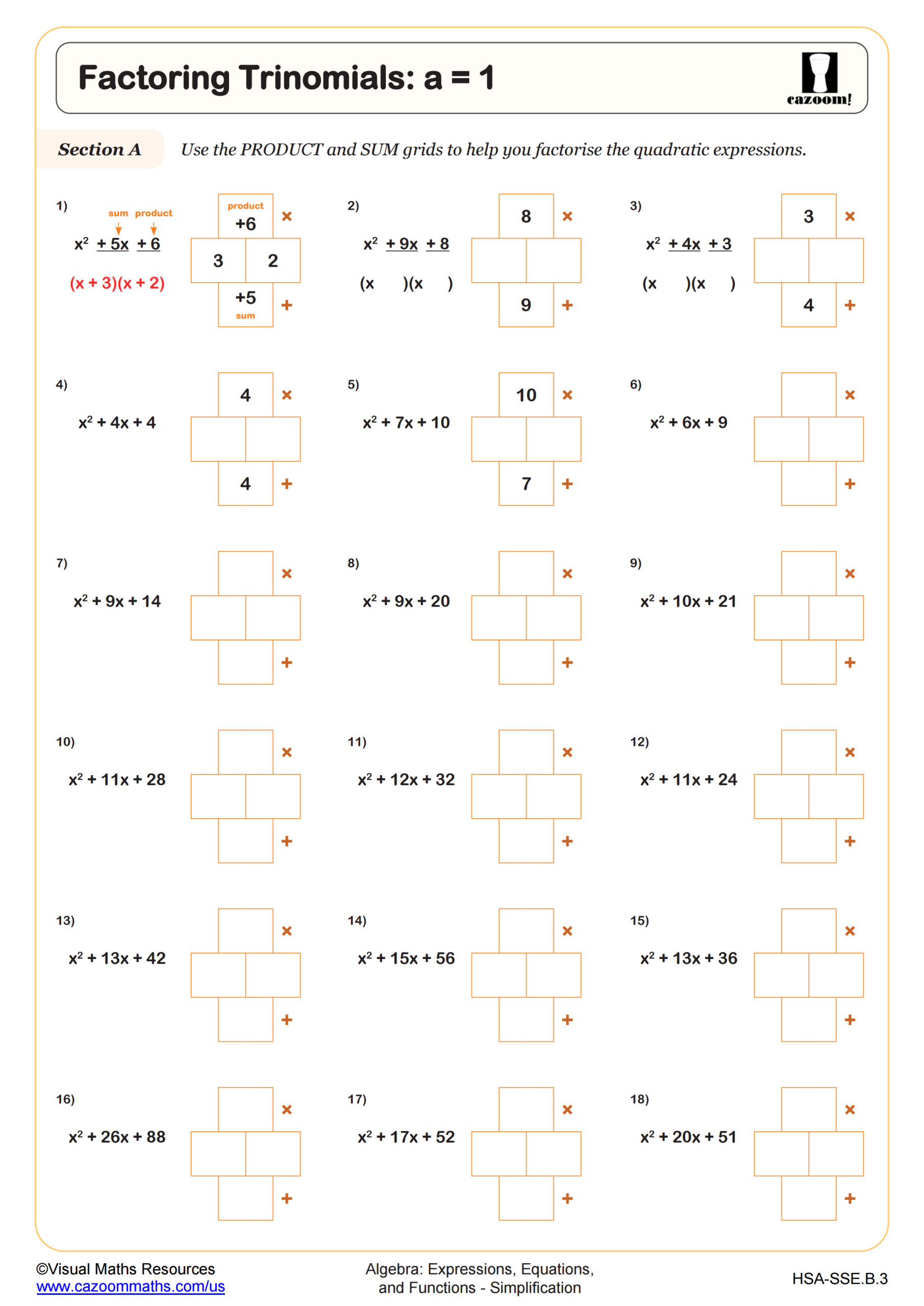
Factoring Trinomials: a = 1
Factoring using GCF

Factoring: Difference of Two Squares

Greatest Common Factor

Identifying Like Terms

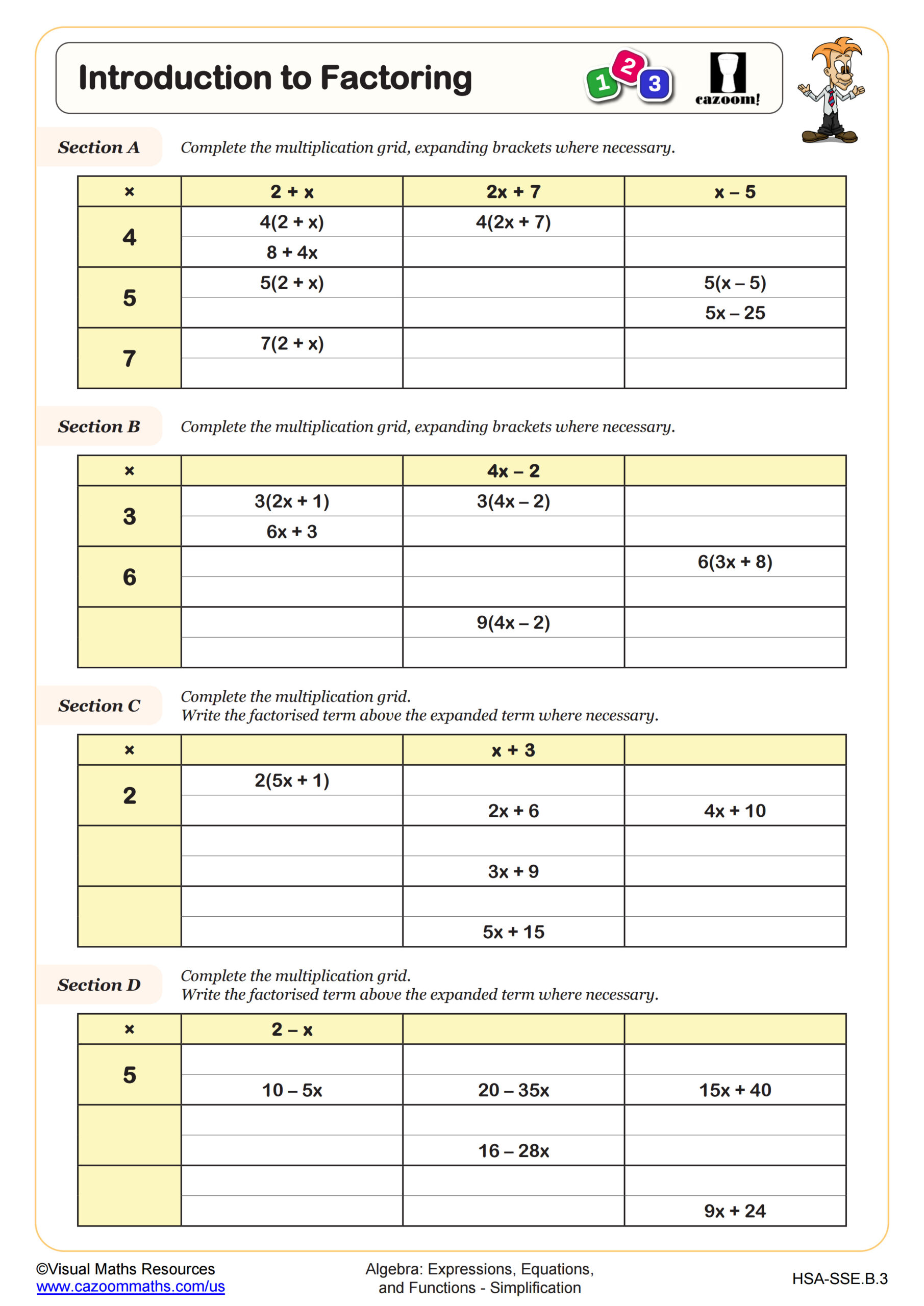
Introduction to Factoring
Multiply and Divide Algebraic Fractions (A)
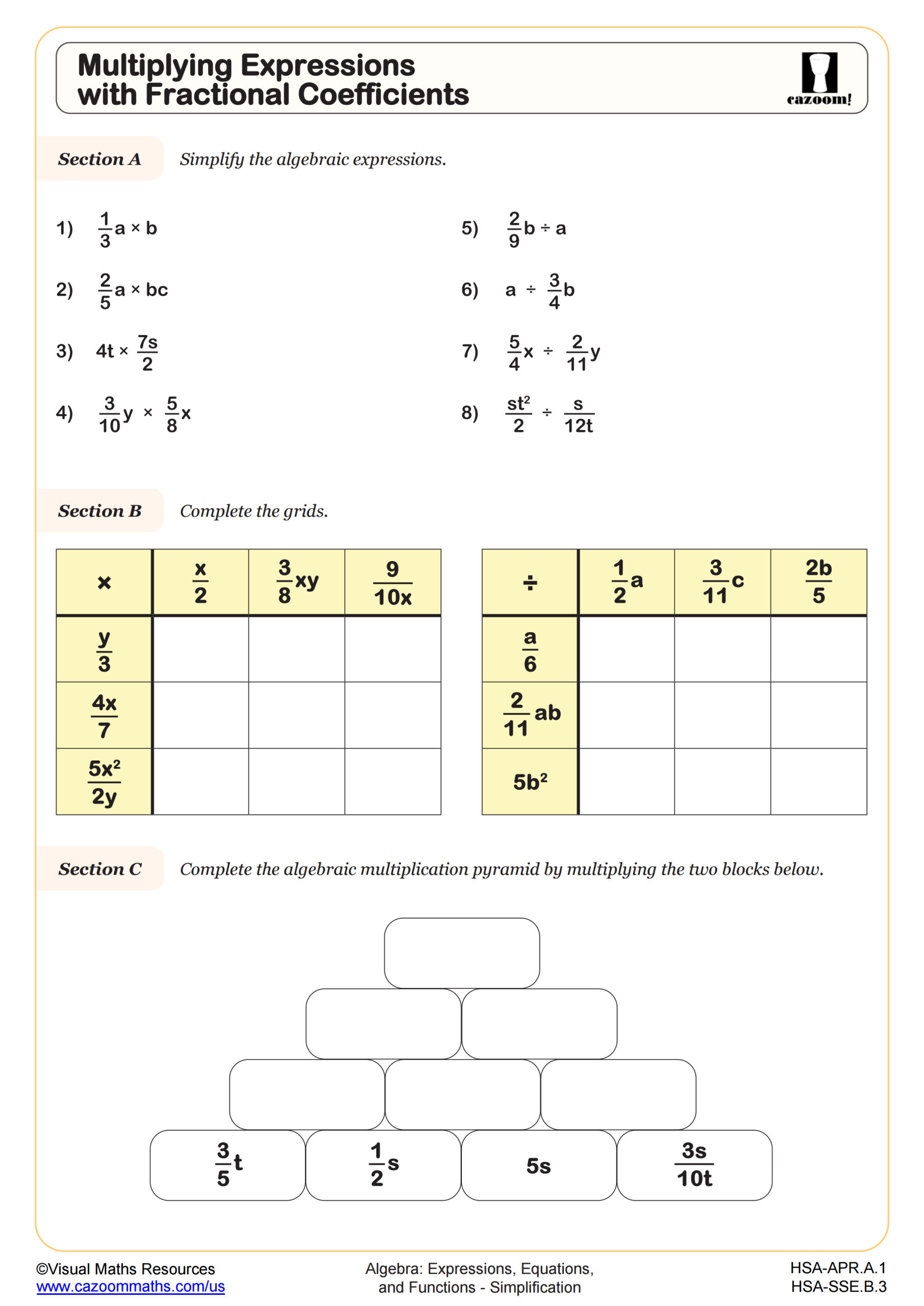
Multiplying Expressions with Fractional Coefficients
Polynomial Addition Perimeters
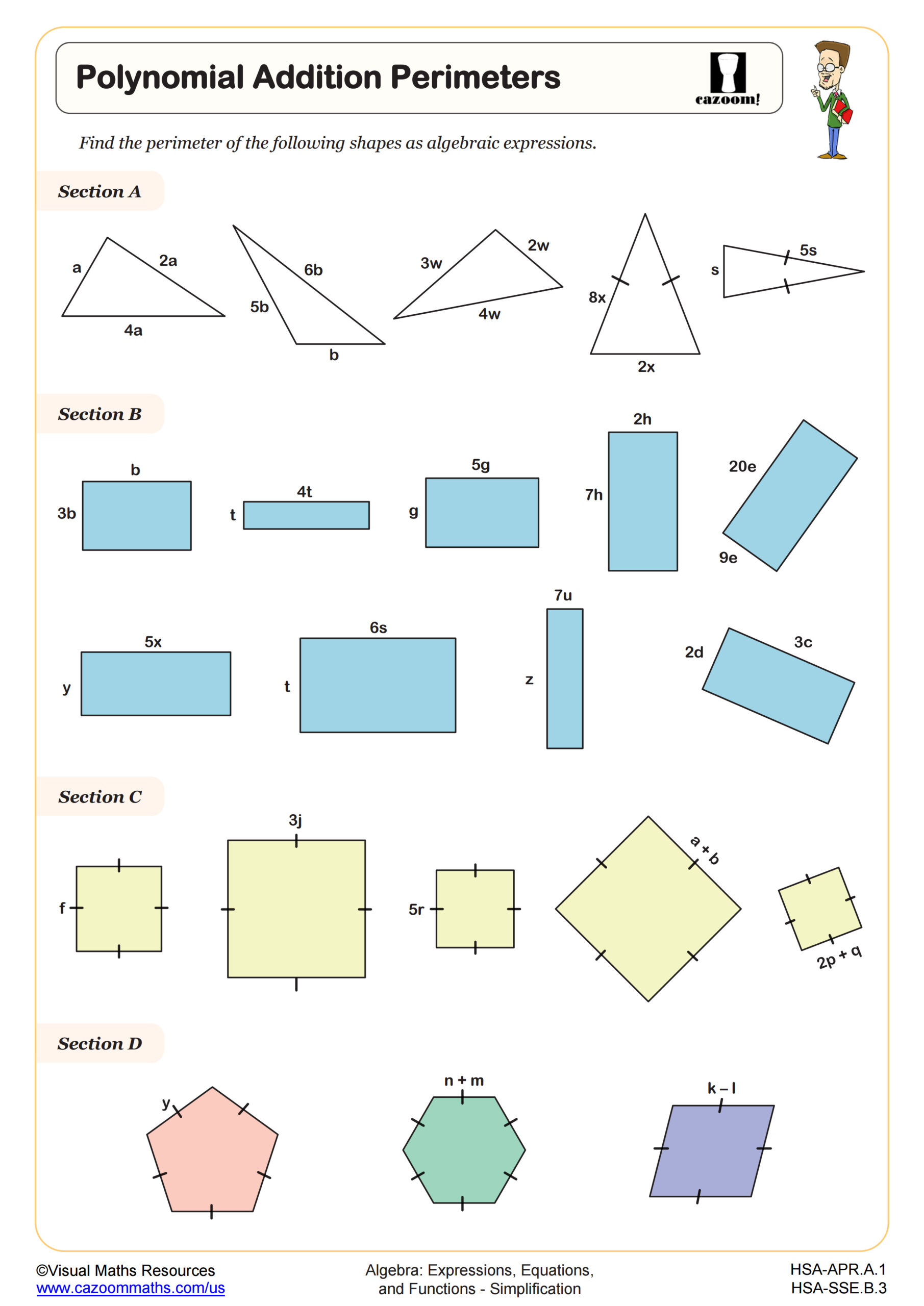
Polynomial Addition Pyramids (A)
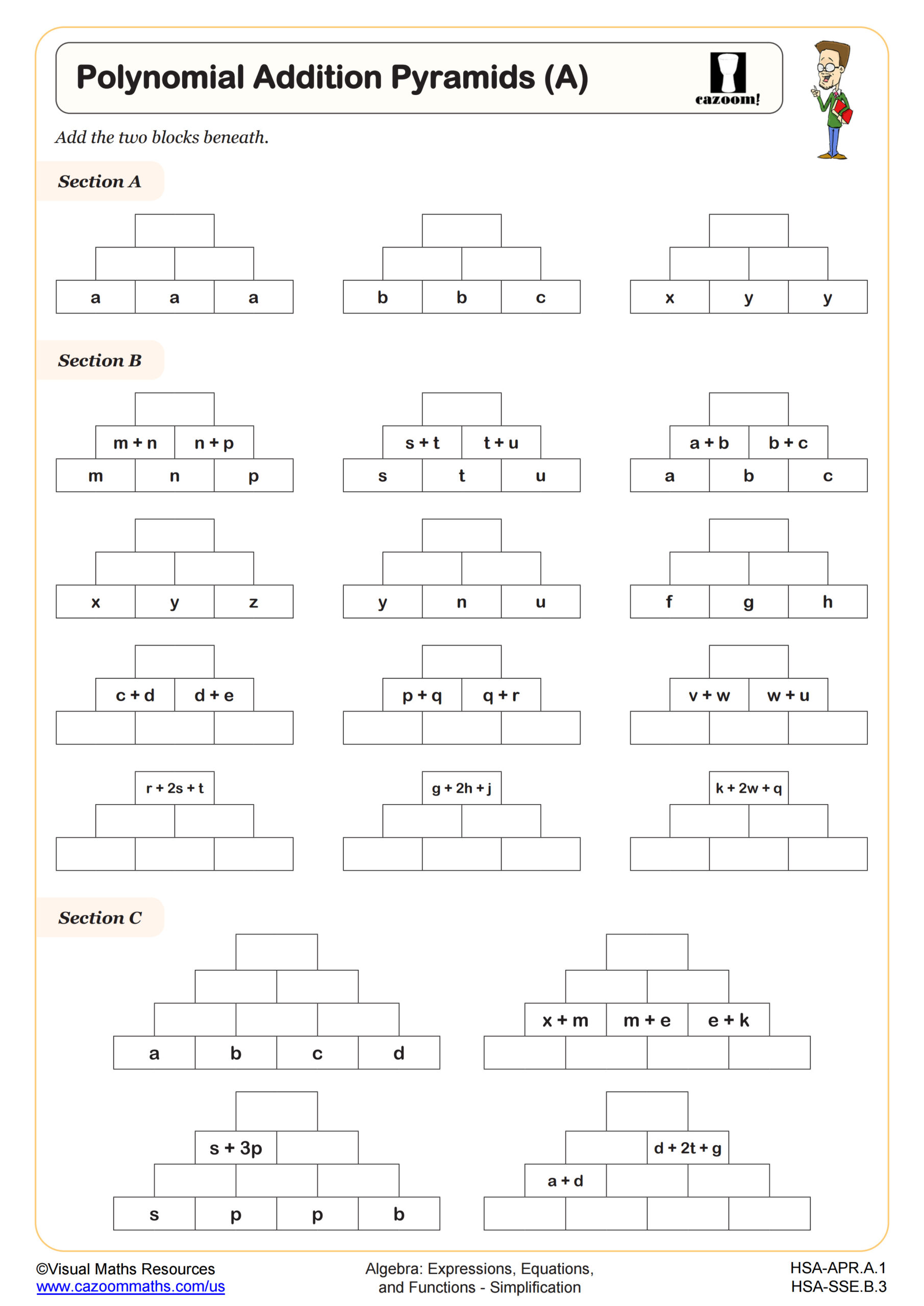
Polynomial Addition Pyramids (B)
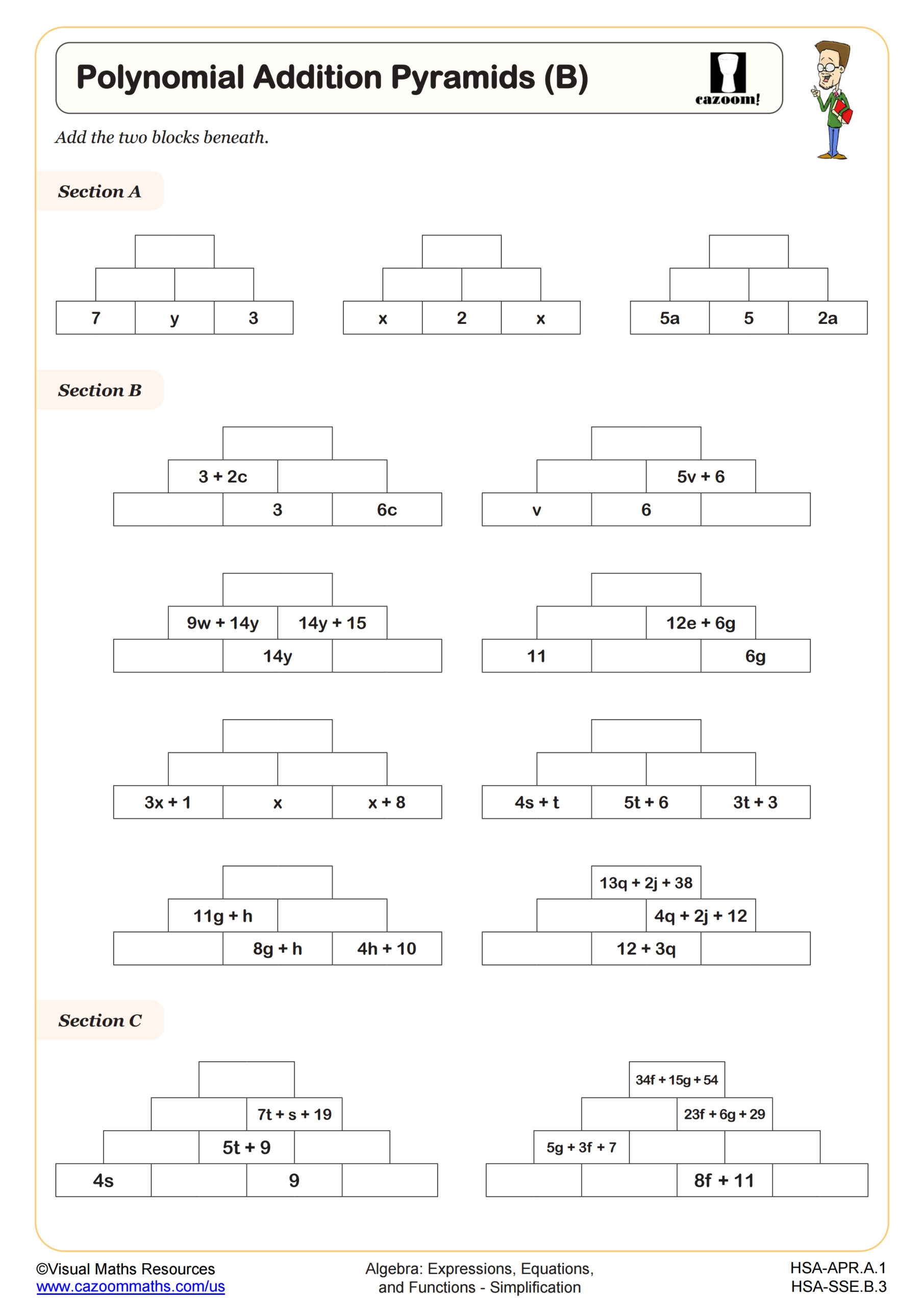
Polynomial Addition Pyramids (C)
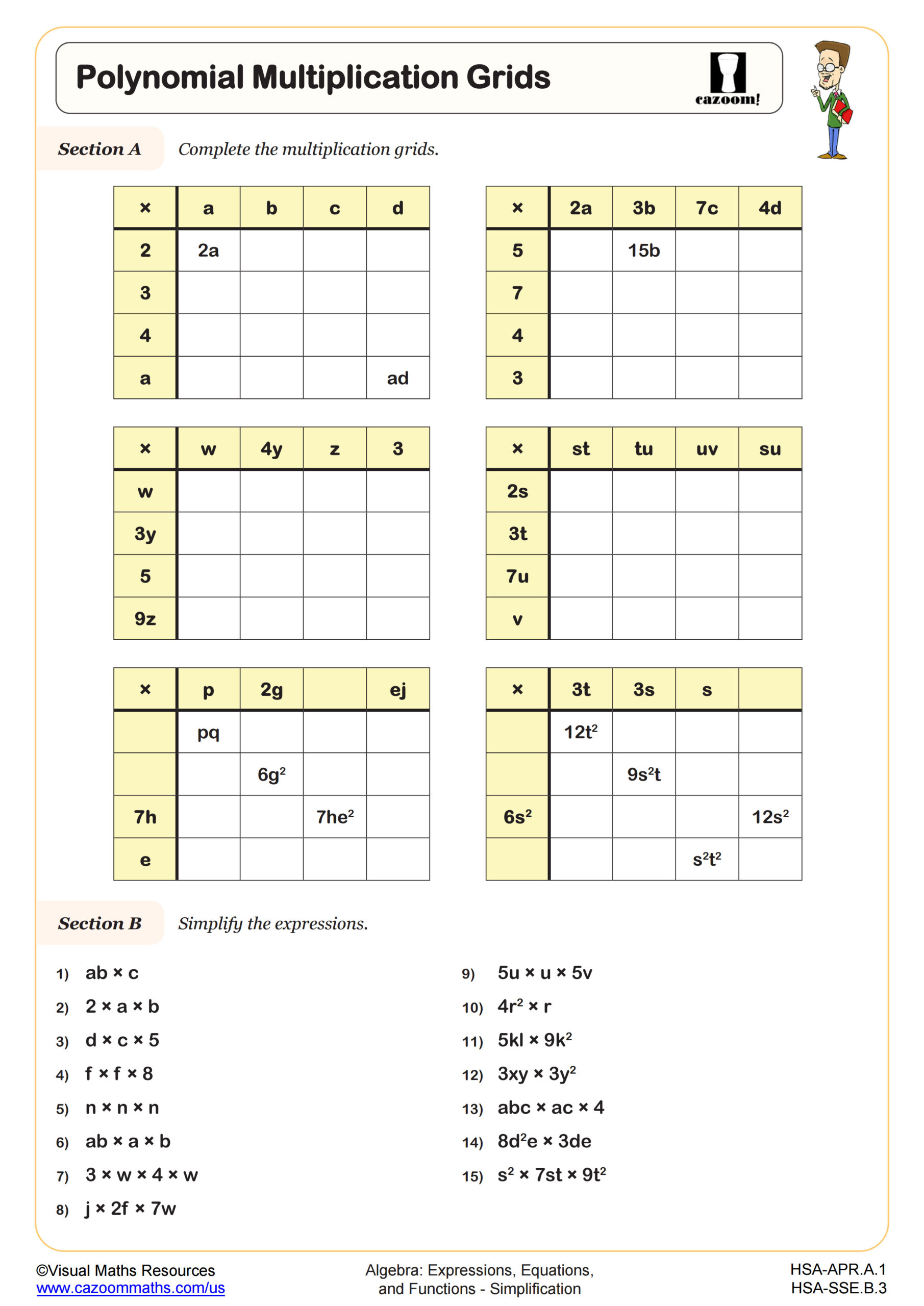
Polynomial Multiplication Grids
Proving Equivalent Expressions

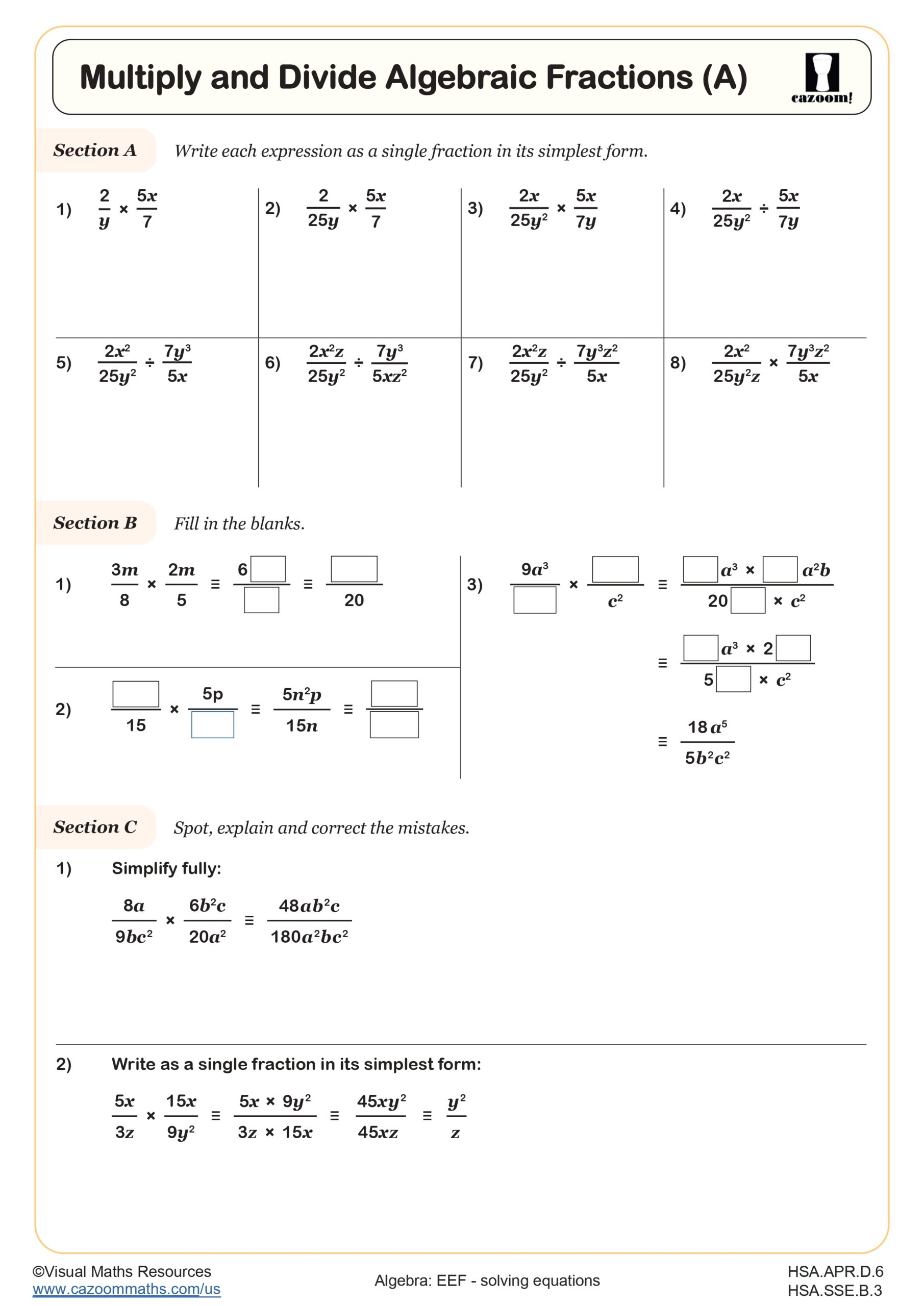
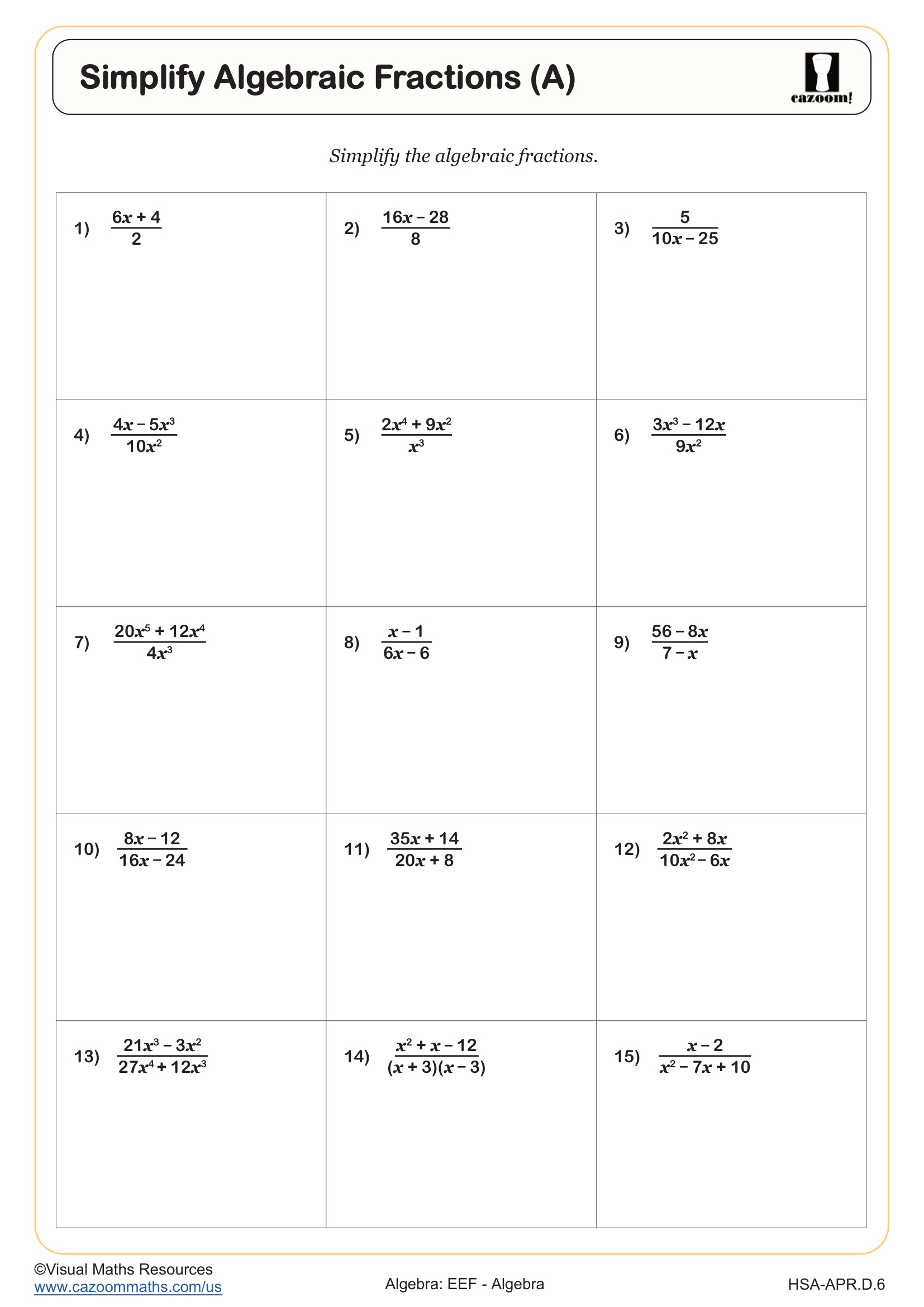
Simplify Algebraic Fractions (A)
Simplify Algebraic Fractions (B)

Simplifying Expressions by Combining Like Terms

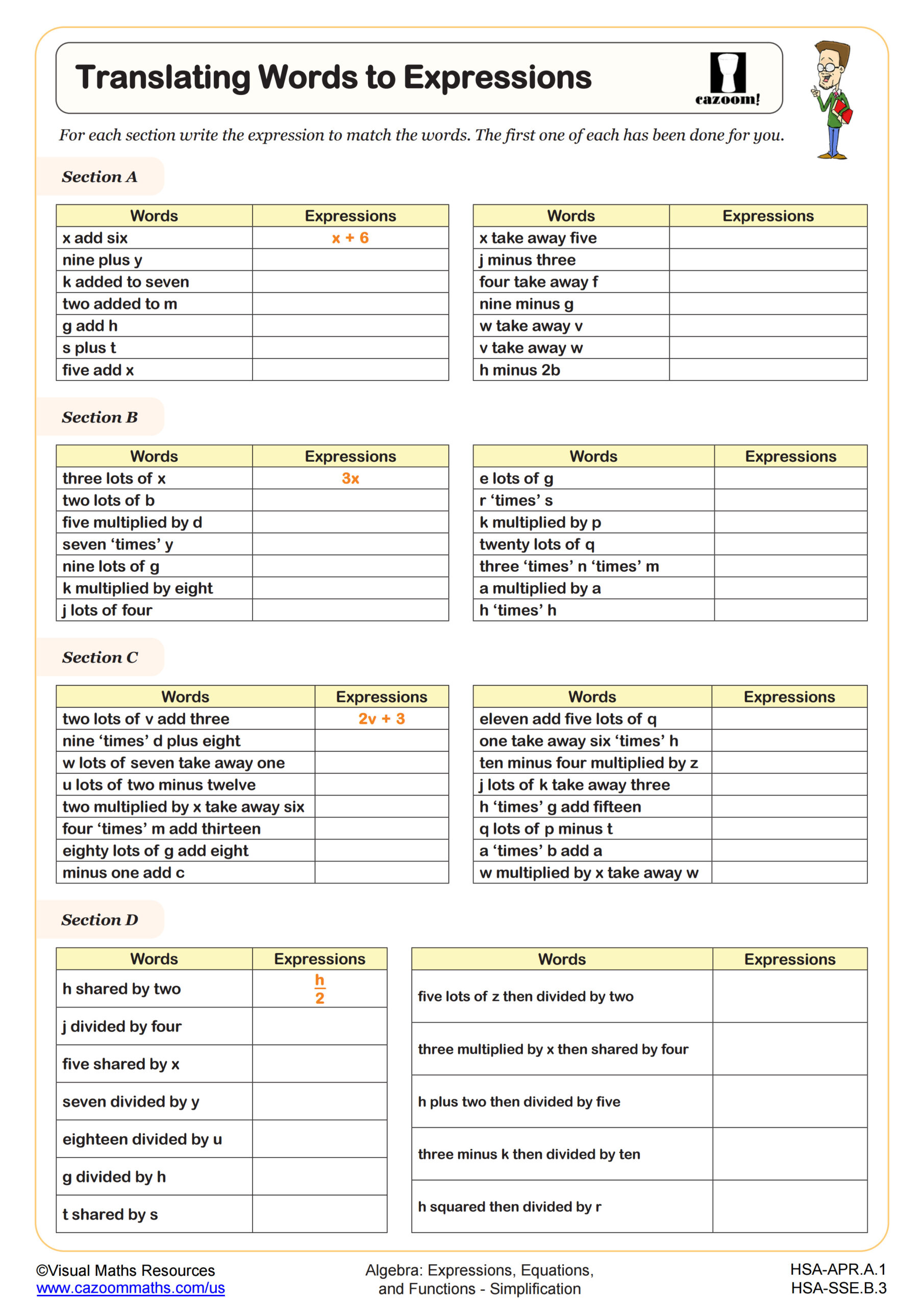
Translating Words to Expressions
Writing Expressions: Thinking of a Number

What Does Simplification Cover in Integrated Math 1?
Simplification in Integrated Math 1 encompasses identifying and combining like terms, factoring expressions using the greatest common factor, and performing operations with polynomials. Students learn to recognize variable terms with identical components, understand how coefficients behave during addition and subtraction, and apply the distributive property in reverse when factoring. This aligns with Common Core standards for seeing structure in expressions and performing arithmetic operations on polynomials.
A common misconception occurs when students attempt to combine unlike terms such as 3x and 3x², treating them as equivalent because the coefficients match. Students lose significant points on assessments when they simplify 2x + 3y to 5xy or combine terms across different variables. Teachers find that color-coding like terms during initial instruction helps students visually distinguish which terms can be combined, creating a lasting mental framework for accurate simplification.
How Does Simplification Appear on the SAT and State Assessments?
Standardized tests like the SAT and ACT embed simplification within multi-step problems rather than testing it in isolation. Students must simplify algebraic expressions before solving equations, manipulate polynomial expressions within word problems, and factor expressions to identify equivalent forms. State assessments aligned with Common Core standards expect students to demonstrate fluency with combining like terms and recognizing algebraic structure without computational aids.
Students frequently lose points when they rush through simplification as a preliminary step, making sign errors when subtracting polynomials or incorrectly distributing negative signs. Teachers notice that assessment questions often place simplified answer choices alongside common incorrect simplifications, rewarding students who carefully track coefficients and signs. Practice with polynomial perimeters and addition pyramids builds the pattern recognition skills that help students avoid these testing pitfalls under time pressure.
What Role Does the Greatest Common Factor Play in Simplification?
Factoring using the greatest common factor represents reverse simplification, where students identify the largest expression that divides evenly into all terms of a polynomial. This skill requires recognizing common numerical factors, shared variables, and the lowest exponent among like variables. Students learn to extract the GCF from expressions like 12x³ + 18x² by identifying both the numerical GCF (6) and variable component (x²), rewriting the expression as 6x²(2x + 3).
This technique connects directly to real-world applications in engineering and design, where professionals factor expressions to find dimensions or optimize measurements. For instance, architects determining tile arrangements or computer scientists optimizing code efficiency both rely on factoring principles. College-bound students encounter GCF factoring again in precalculus when simplifying rational expressions and in calculus when finding antiderivatives, making early mastery particularly valuable for STEM pathways.
How Can Teachers Use These Simplification Worksheets in Integrated Math 1?
The worksheets provide scaffolded practice that builds from identifying like terms through complex polynomial operations and factoring. Visual formats like addition pyramids challenge students to work backward from simplified results, strengthening their understanding of how terms combine. Perimeter problems contextualize simplification within geometric applications, helping students see algebraic manipulation as a tool rather than an abstract exercise. The variety of approaches prevents the mechanical repetition that often leads to disengagement.
Teachers use these resources effectively for differentiated instruction, assigning foundational worksheets for students struggling with term identification while providing pyramid challenges for those ready for problem-solving applications. The complete answer keys make the worksheets suitable for independent test review, homework with immediate feedback options, or warm-up activities that activate prior knowledge before new lessons. Paired work with these materials encourages mathematical discourse as students explain their simplification steps to partners, deepening conceptual understanding beyond procedural execution.