Integrated Math 1 Transformations Worksheets
What Do Integrated Math 1 Students Learn About Transformations?
In Integrated Math 1, students learn to perform and describe the four rigid transformations (translations, reflections, rotations, and dilations) in the coordinate plane. The curriculum emphasizes understanding transformations as functions that take points as inputs and produce new points as outputs, aligning with Common Core standards for congruence and geometric modeling. Students work with transformation notation, identify corresponding parts of figures, and determine whether transformations preserve size and shape.
A common error occurs when students attempt rotations: many assume a 90-degree rotation always moves a point from Quadrant I to Quadrant II, forgetting that the direction (clockwise versus counterclockwise) and center of rotation matter tremendously. Teachers often use tracing paper or patty paper to help students physically rotate figures, which builds intuition before moving to algebraic rules. Students also practice composing multiple transformations, recognizing that order affects the final image position.
How Do Transformations Appear on the SAT and State Assessments?
Standardized tests assess transformations through multiple-choice and grid-in questions that require students to identify coordinates after transformations, determine which transformation maps one figure onto another, or recognize properties preserved under specific transformations. The SAT particularly tests whether students understand that rigid transformations preserve distance and angle measures, while dilations preserve angle measures but change side lengths proportionally. Questions often embed transformations within coordinate geometry contexts or ask students to justify congruence claims.
Students lose points when they apply transformation rules mechanically without checking their work against the coordinate plane grid. For example, when reflecting across the y-axis, students might correctly change the sign of the x-coordinate but then plot the point in the wrong quadrant due to careless errors. State assessments increasingly require written explanations of why two figures are congruent through a sequence of transformations, demanding both procedural fluency and conceptual understanding.
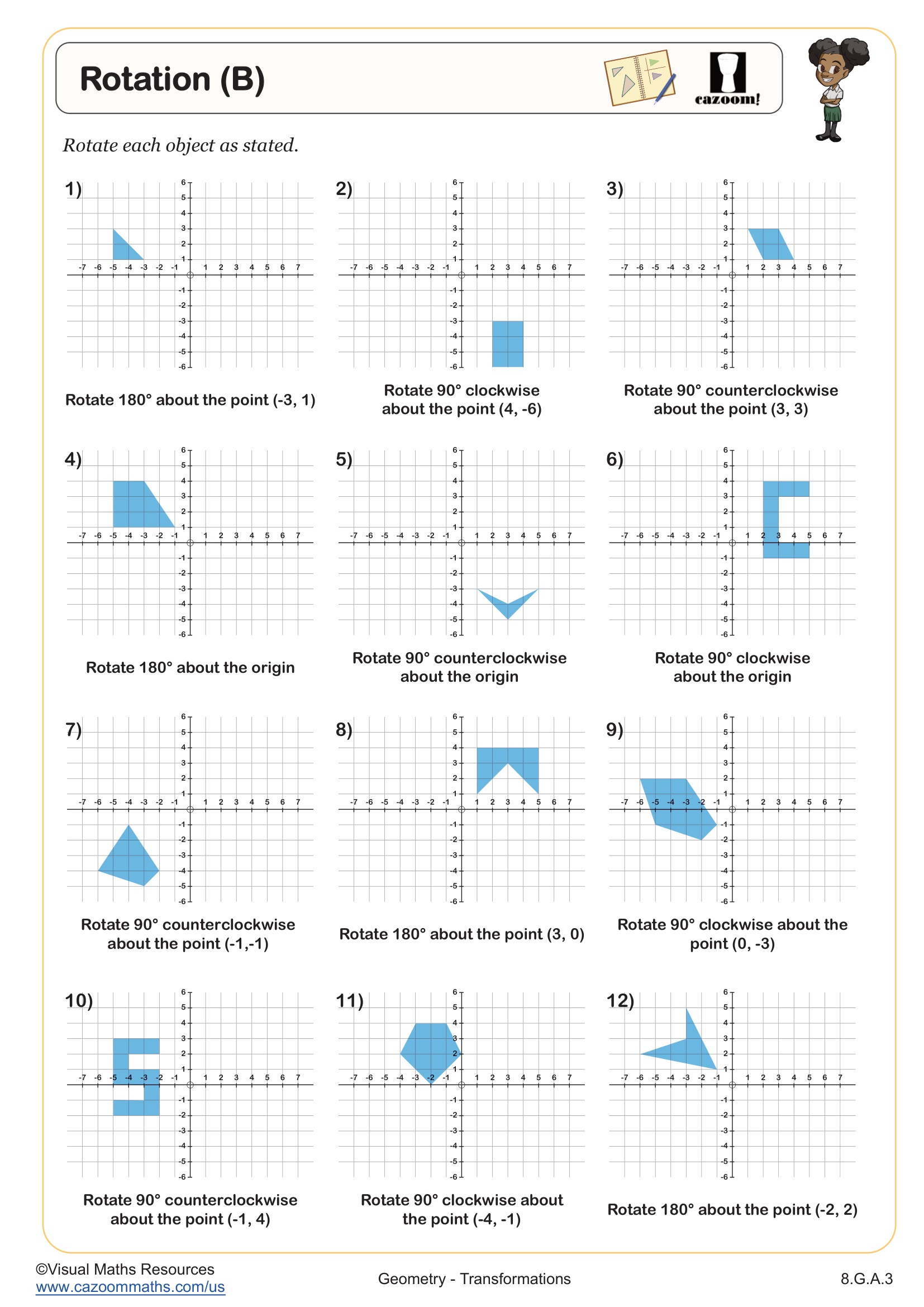
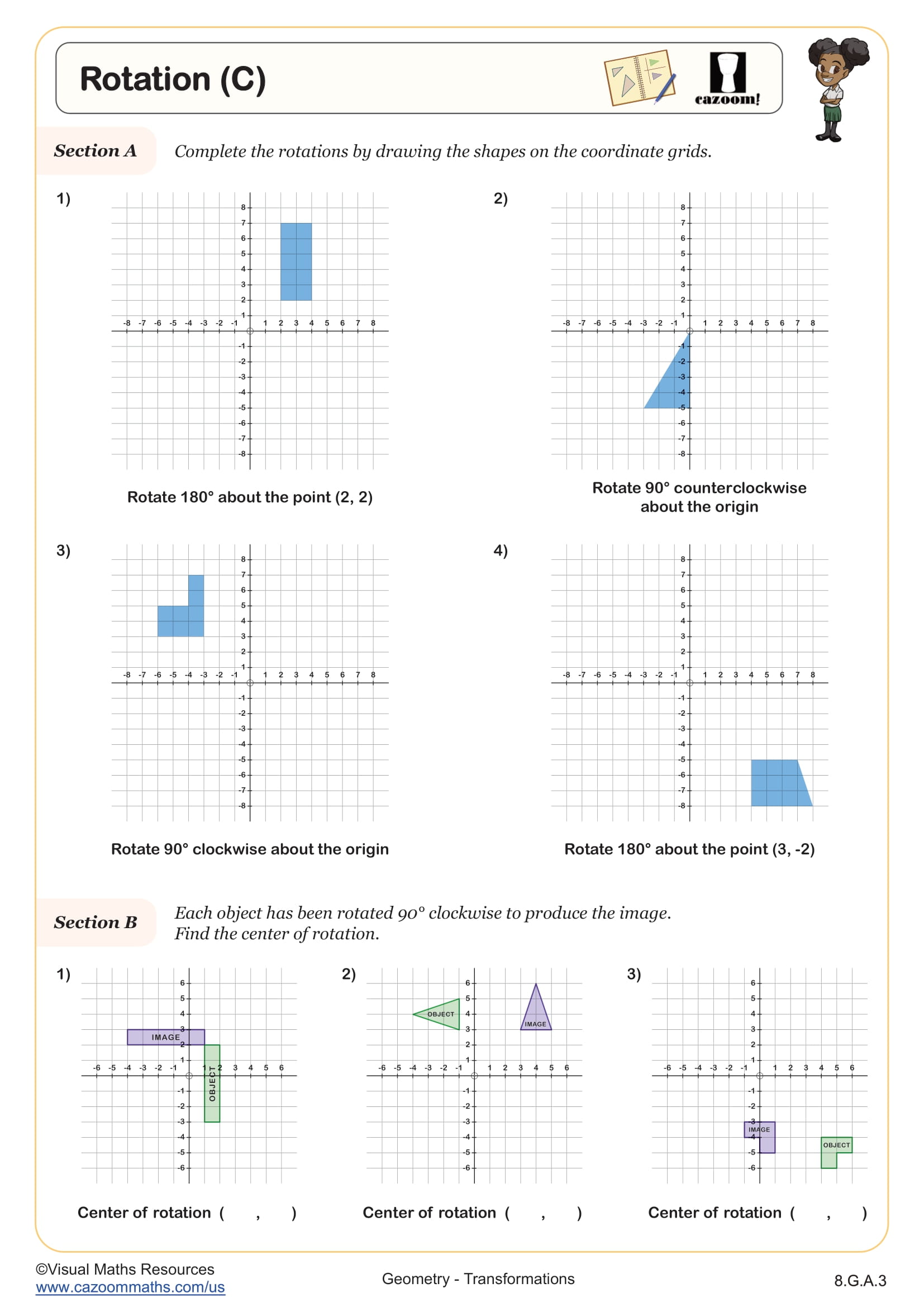
What Rotation Techniques Do Students Practice in These Worksheets?
Rotation worksheets focus on turning figures around a fixed point, typically the origin, by specific angle measures (90°, 180°, 270°). Students learn rotation rules for common angles and practice identifying the center and angle of rotation by comparing pre-images to images. The worksheets progress from rotations of individual points to complete polygons, helping students visualize how entire shapes transform while maintaining their size and shape. Teachers notice that students grasp rotations more quickly when they first master the concept that a 180-degree rotation maps (x, y) to (−x, −y), which many students recognize as simply "flipping both signs."
Rotations appear frequently in computer graphics, game design, and engineering applications where objects must turn around axes. Robotics programs rely on precise rotation calculations to move mechanical arms to specific positions. In architecture, understanding rotational symmetry helps designers create aesthetically balanced structures. College-bound students pursuing STEM fields encounter rotations again in physics (angular motion), computer science (image processing), and higher-level mathematics (transformation matrices).
How Can Teachers Use These Integrated Math 1 Transformation Worksheets?
These worksheets provide structured practice that builds from basic rotation concepts to more complex applications, allowing teachers to differentiate instruction based on student readiness. Each worksheet includes problems at varying difficulty levels, making them suitable for whole-class instruction, small-group work, or independent practice. The answer keys enable students to check their understanding immediately, which helps them identify misconceptions before they become ingrained. Teachers can assign specific worksheets as formative assessments to gauge whether students are ready to move from concrete examples to abstract transformation rules.
Many teachers use these worksheets for spiraled review throughout the semester, since transformation concepts connect to later topics like congruence proofs and similarity. They work particularly well as warm-up activities before lessons on symmetry or as test preparation when reviewing geometric properties. Some teachers assign worksheets as paired activities where one student performs the transformation while their partner verifies using graph paper, promoting mathematical discourse. The downloadable PDF format allows teachers to print copies for in-class practice or share digitally for remote learning situations.