Integrated Math 2 Algebra Worksheets
Add and Subtract Algebraic Fractions (B)

Finding Inverse Functions - Using Function Machines

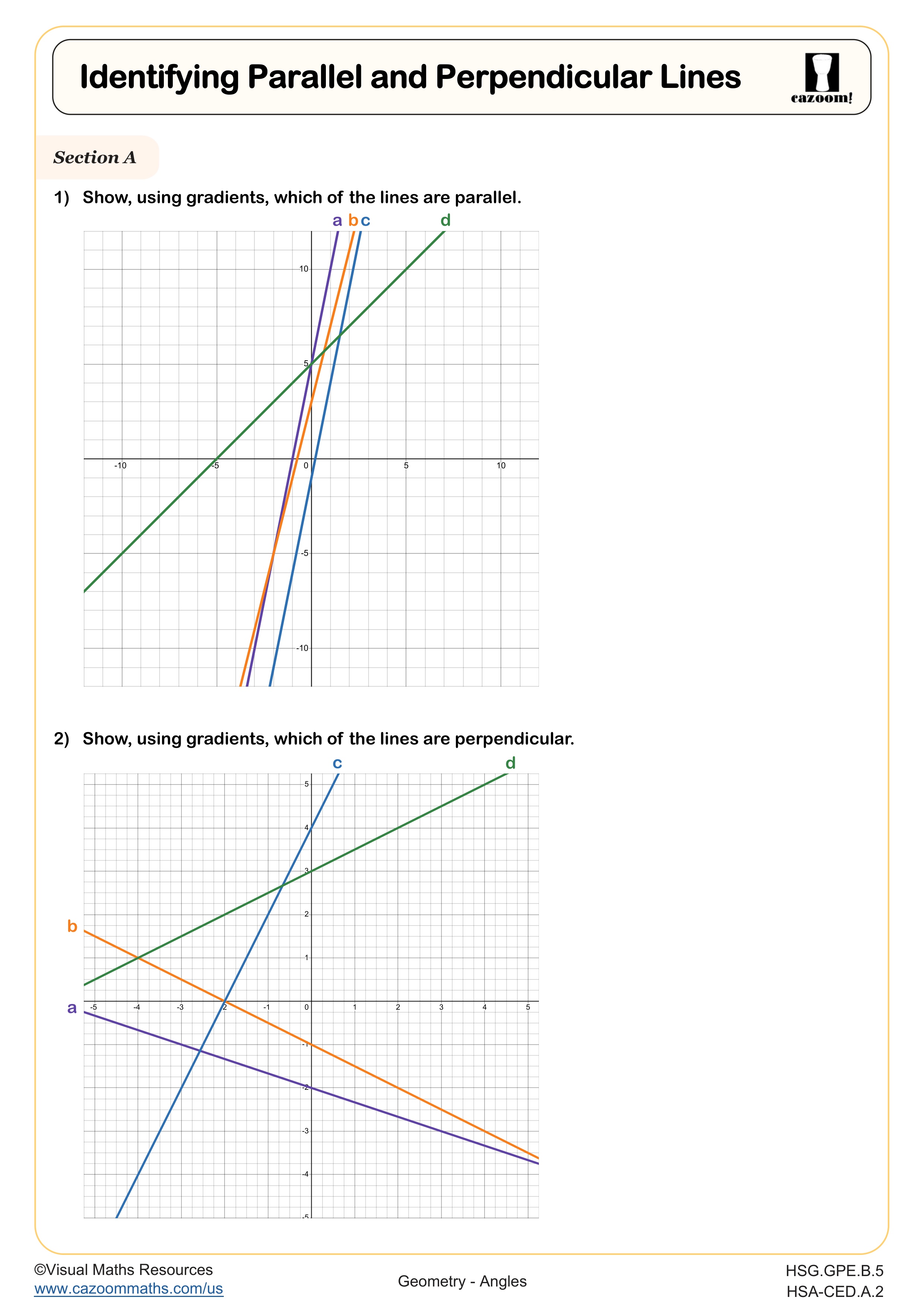
Identifying Parallel and Perpendicular Lines
Introducing Functions - Using Function Machines

Multiply and Divide Algebraic Fractions (B)

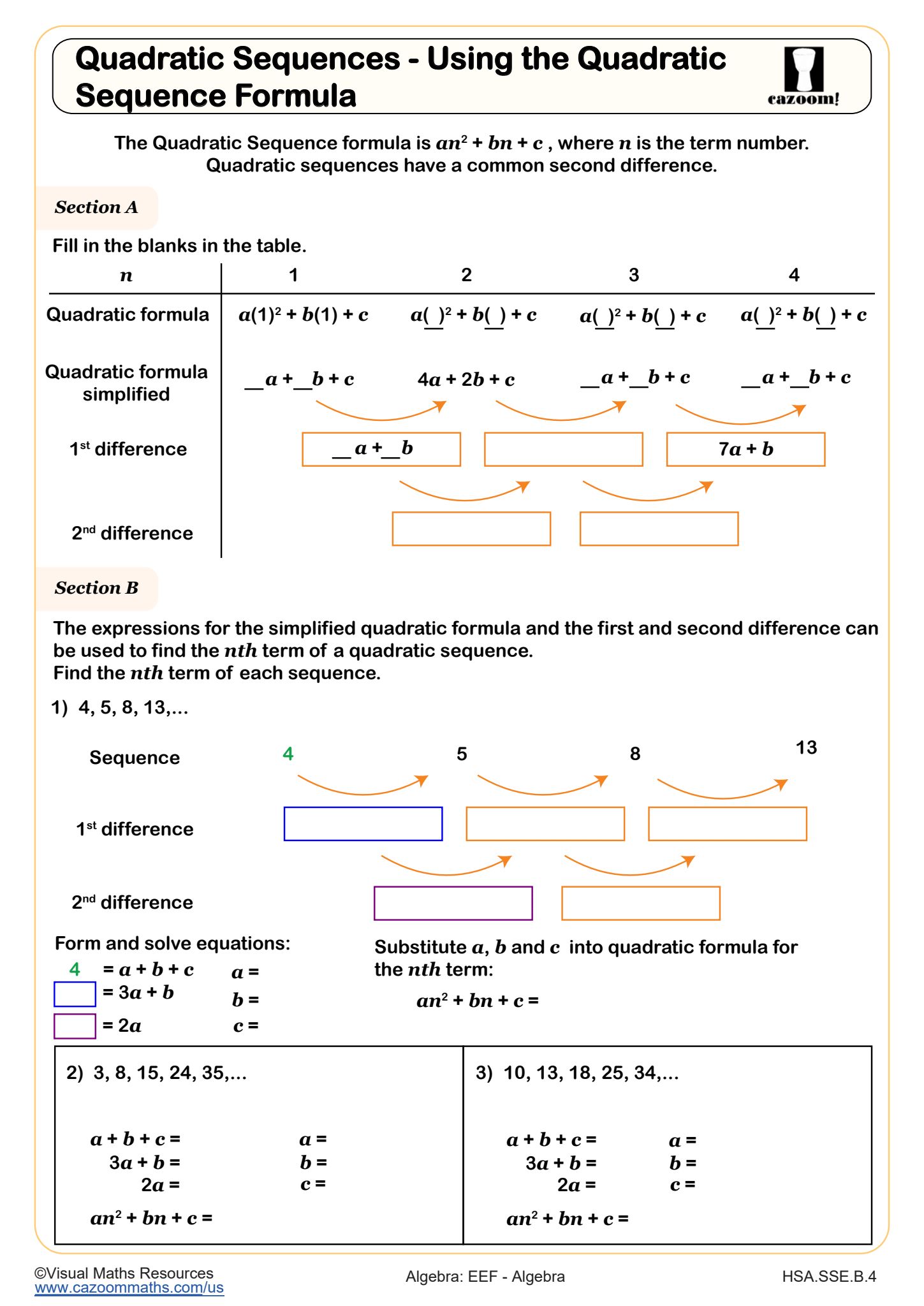
Quadratic Sequences - Using the Quadratic Sequence Formula
Rationalizing the Denominator - with Binomial Numerators

Solving Quadratic Equations (E) - Using all Three Methods

Solving Systems of Linear Equations - Using Bar Models

What algebra topics are covered in Integrated Math 2?
Integrated Math 2 algebra extends beyond basic equation solving to include rational expressions, function notation, systems of equations, and linear relationships in coordinate geometry. Students work with algebraic fractions, learning to multiply, divide, add, and subtract rational expressions while finding common denominators and simplifying results. The course introduces formal function notation and different representations, including function machines that help students visualize input-output relationships. Systems of linear equations receive deeper treatment through multiple solution methods, and coordinate geometry connects algebra to geometric concepts through slope relationships.
A common misconception surfaces when students treat algebraic fractions like numeric fractions without considering restrictions on variables. Teachers frequently remind students that denominators cannot equal zero, requiring them to identify excluded values before simplifying. This attention to domain restrictions becomes increasingly important as students progress toward rational functions in later courses.
How do these algebra skills appear on the SAT and ACT?
Standardized tests assess rational expression operations through multi-step problems that require simplification before solving equations. The SAT frequently presents systems of equations in context, asking students to interpret what the solution represents in a real-world scenario. Function notation appears throughout both tests, with questions requiring students to evaluate compositions, find inverse relationships, or interpret function behavior from graphs or tables. Questions about parallel and perpendicular lines often combine slope concepts with equation writing, testing whether students recognize that parallel lines share identical slopes while perpendicular lines have negative reciprocal slopes.
Students lose points when they incorrectly cancel terms across addition or subtraction in algebraic fractions, treating them like factors in multiplication. Another frequent error occurs when students forget to distribute negative signs when subtracting fractions, leading to sign errors in the numerator. Time pressure on standardized tests makes these procedural mistakes more common, particularly when students haven't developed fluency through adequate practice.
What strategies help students master operations with algebraic fractions?
Operations with algebraic fractions follow the same principles as numeric fractions but require factoring skills and attention to variable restrictions. For multiplication and division, students factor all numerators and denominators completely, then cancel common factors before multiplying across. Addition and subtraction require finding the least common denominator by identifying all unique factors from each denominator, then rewriting each fraction with that common denominator before combining numerators. Students confidently tackle these problems once they recognize that factoring must happen first, making common factors visible for cancellation or helping identify the LCD structure.
Rational expressions model real-world rate problems that engineers and scientists encounter regularly. When calculating average speeds for round trips with different rates in each direction, the harmonic mean uses algebraic fractions to find the correct average. Electrical engineers use rational expressions when calculating total resistance in parallel circuits, where the reciprocal of total resistance equals the sum of reciprocals of individual resistances. These applications show students why algebraic fraction skills matter beyond the classroom.
How can teachers use these worksheets effectively in Integrated Math 2?
These worksheets provide scaffolded practice that allows students to build mastery progressively within each algebra topic. The answer keys support multiple teaching approaches, from allowing students to check their own work during independent practice to helping teachers quickly identify common errors during whole-class review. Visual models like bar models for systems of equations and function machines for input-output relationships give students concrete ways to understand abstract concepts before working symbolically. Teachers use the worksheets to differentiate instruction, providing additional support for students who need more practice while offering challenge problems for those ready to extend their thinking.
Many teachers assign these worksheets as warm-up activities to review previously taught concepts or as exit tickets to assess understanding after new instruction. They work well for test preparation, allowing students to practice mixed problems that mirror assessment formats. During intervention periods, teachers use specific worksheets to target identified gaps, while the answer keys enable peer tutoring sessions where students can verify solutions together and discuss different solution approaches.