Integrated Math 2 Circles Worksheets
What Circle Concepts Do Students Learn in Integrated Math 2?
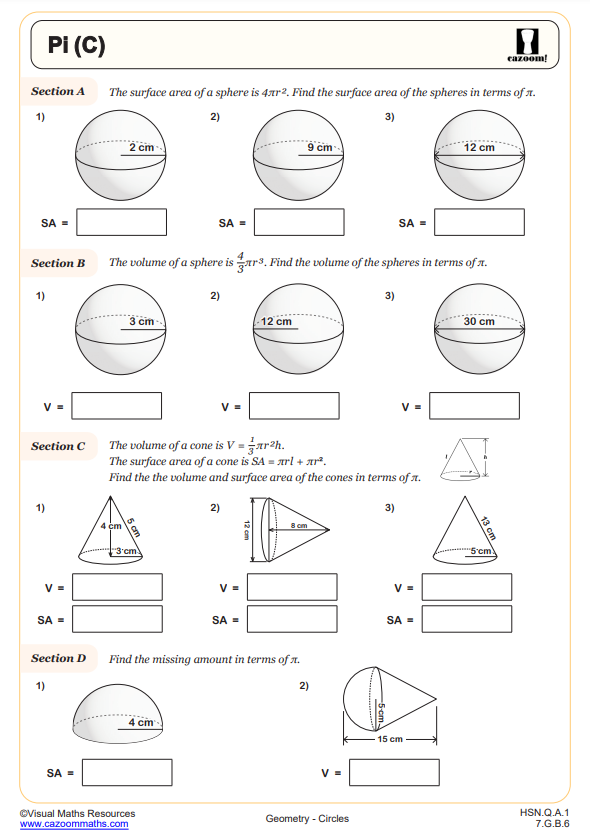
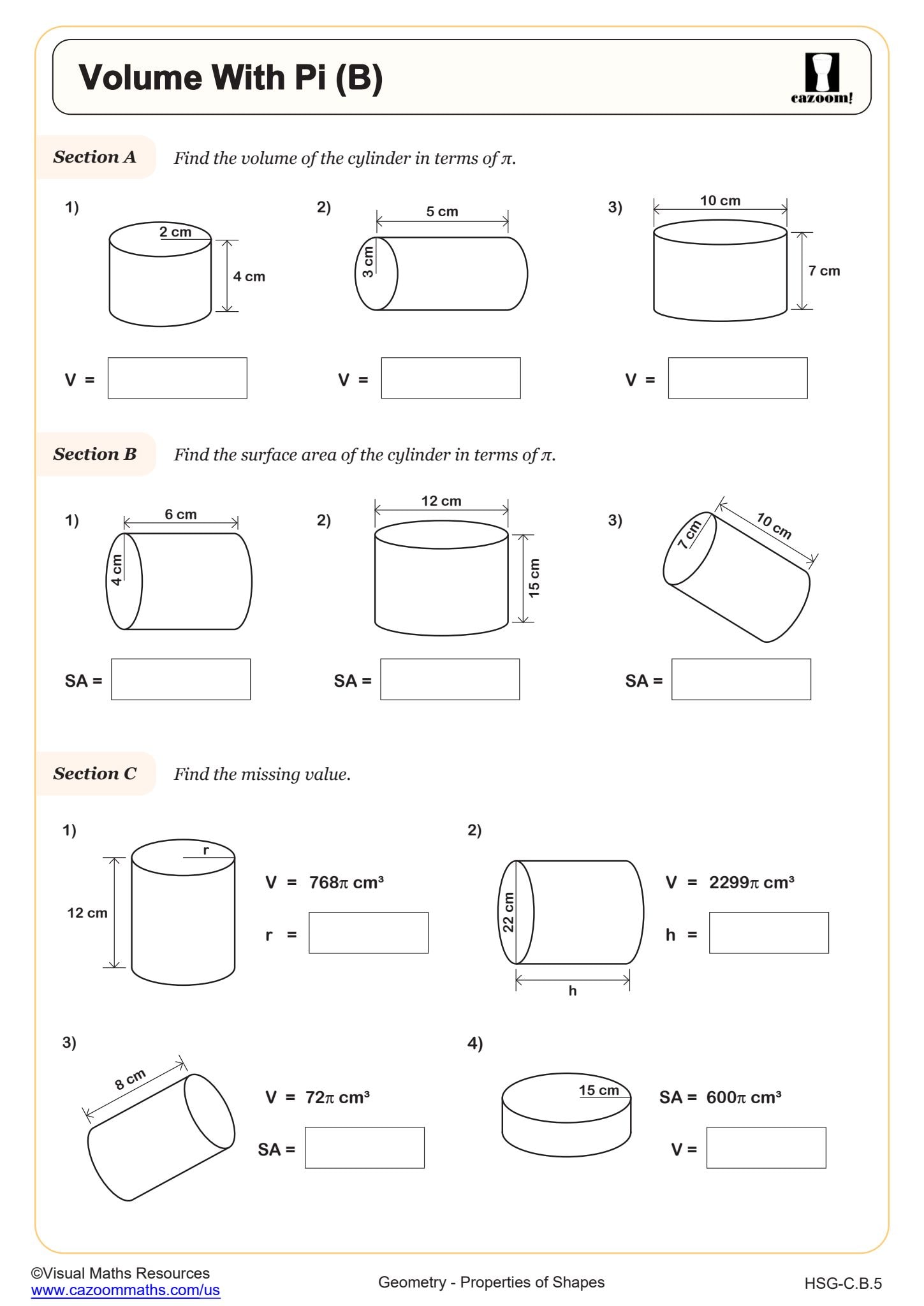
Integrated Math 2 circles curricula emphasize both computational fluency with pi and formal geometric proofs involving circle theorems. Students work with exact values in terms of pi versus decimal approximations, prove theorems about inscribed angles (including angles in the same segment and angles in semicircles), and apply these concepts to three-dimensional volume calculations. This topic typically appears mid-year after students have strengthened their algebraic manipulation skills and basic geometric reasoning.
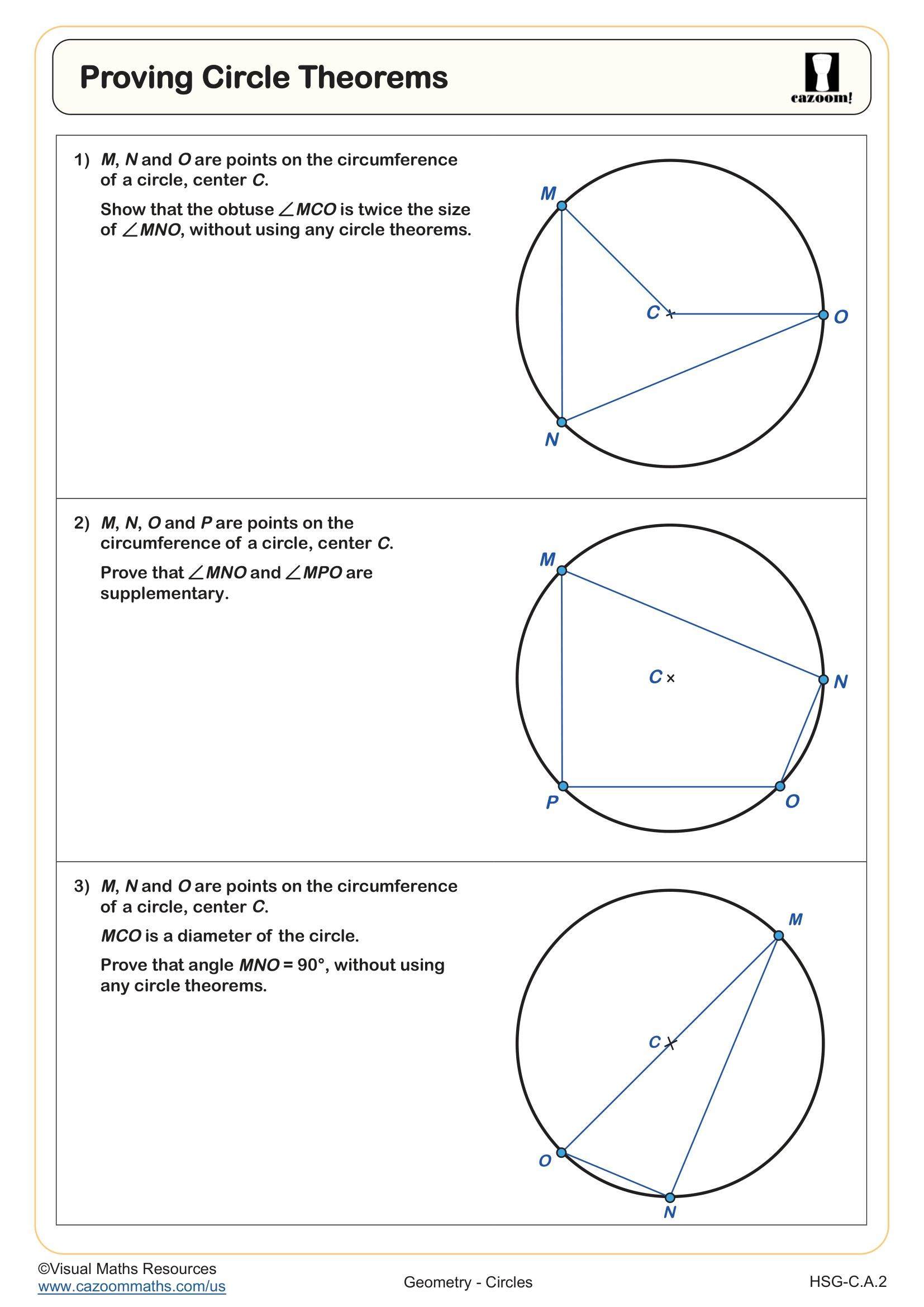
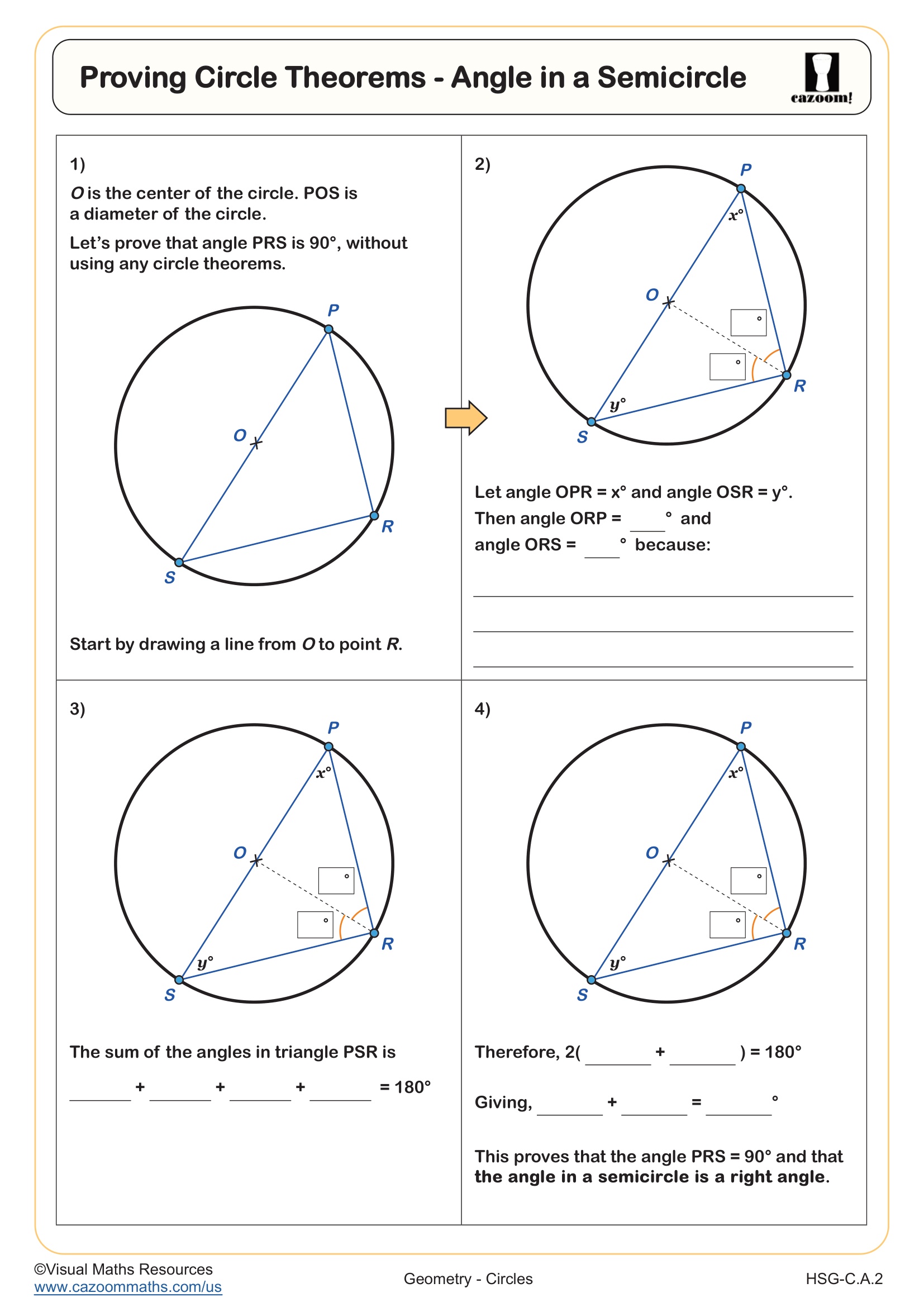
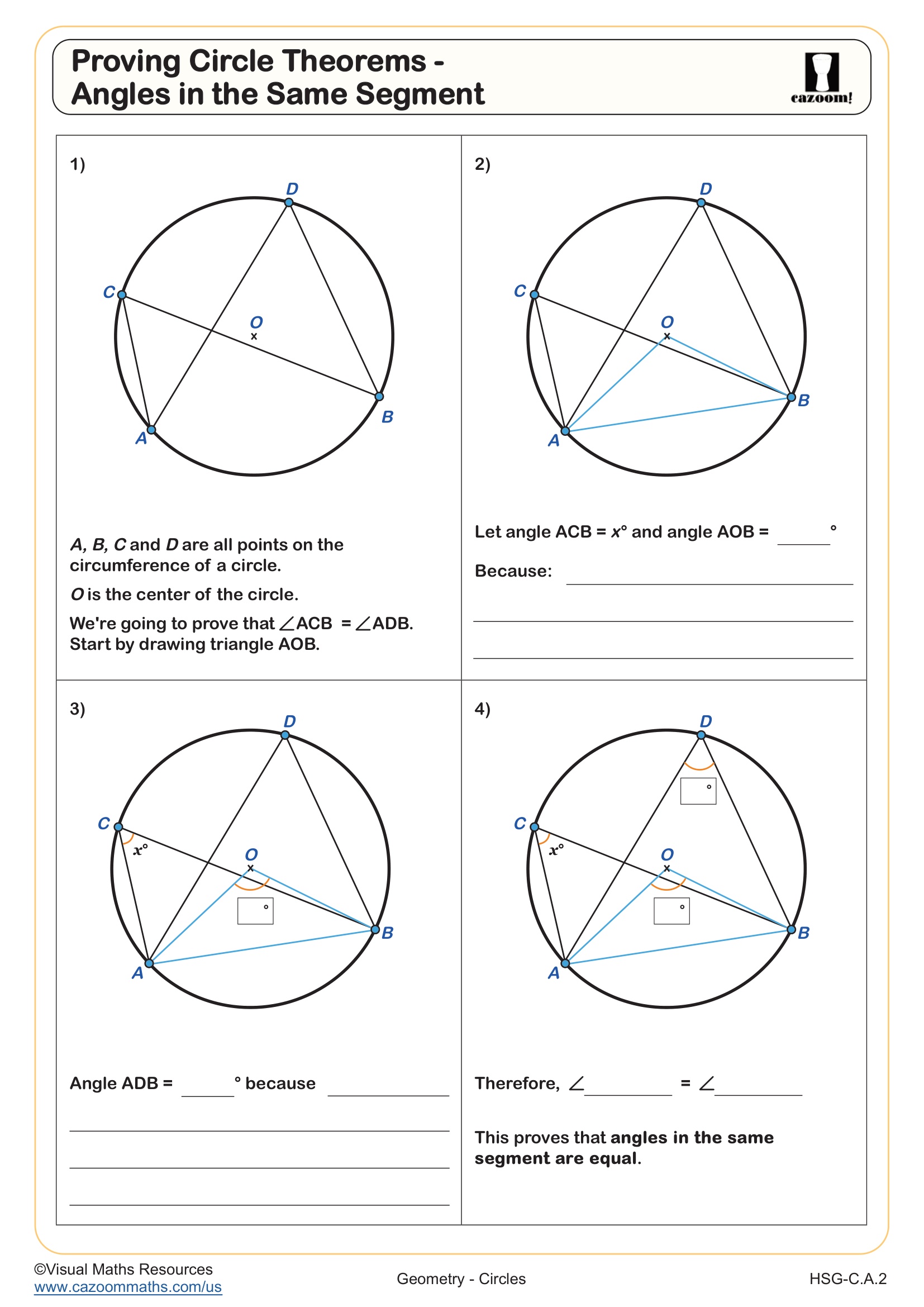
A common misconception emerges when students confuse the angle in a semicircle theorem (always 90 degrees) with angles subtended by other arcs. Teachers observe that students lose points by applying the semicircle theorem to non-diameter chords or by failing to recognize when an inscribed angle and a central angle subtend the same arc. Clear diagrams and systematic labeling help students distinguish between these related but distinct theorems.
How Do Circle Problems Appear on the SAT and ACT?
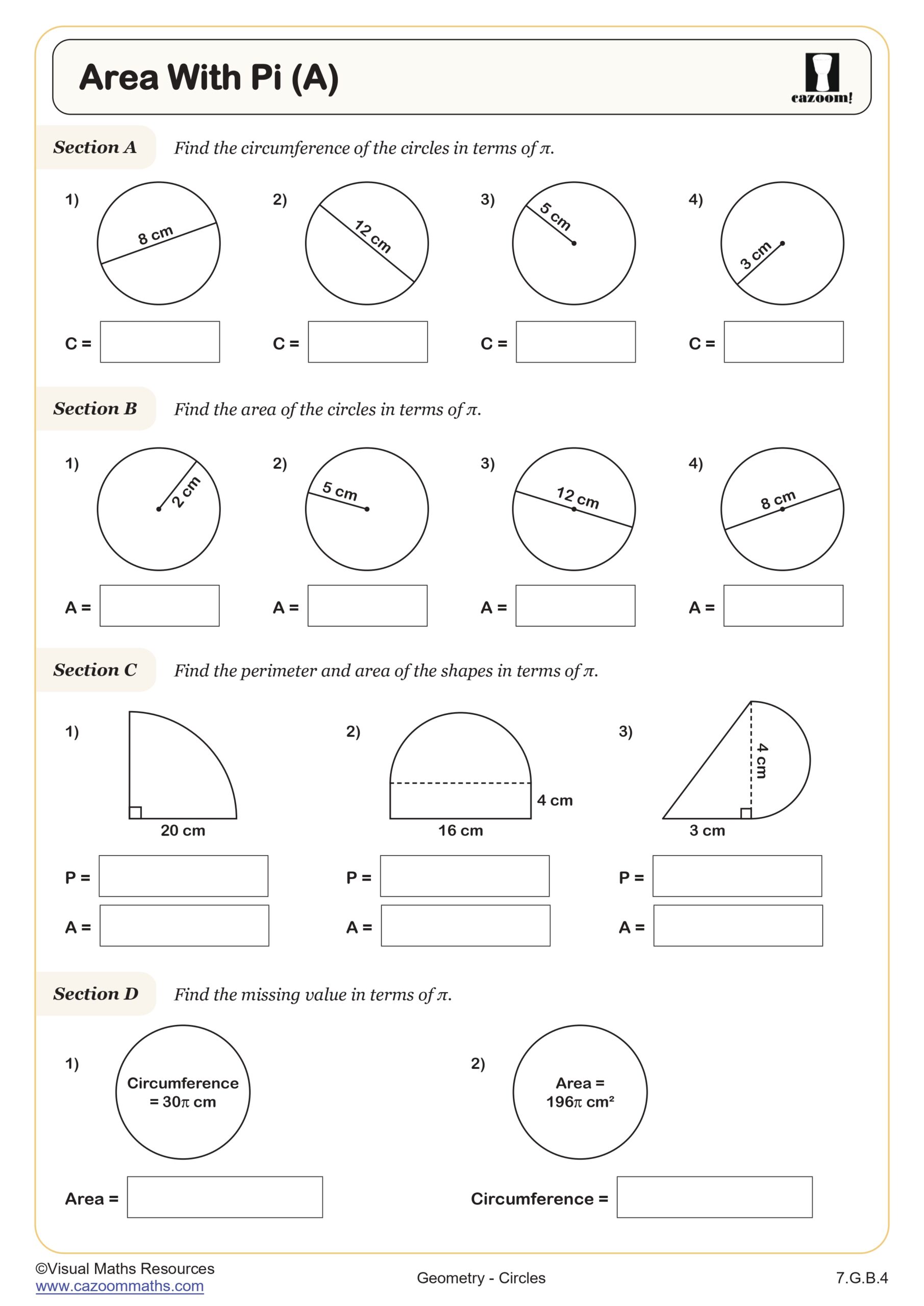
Standardized tests like the SAT and ACT assess circle knowledge through multi-step problems that combine circumference, area, arc length, and sector calculations. Students must demonstrate fluency with both exact answers in terms of pi and decimal approximations. The SAT particularly favors problems connecting circles to coordinate geometry, asking students to determine if a point lies on a circle or to find the center and radius from an equation. ACT problems often embed circle calculations within real-world contexts like wheel rotations or circular garden designs.
Students lose points when they round too early in multi-step calculations or when they forget to convert between radius and diameter. Another frequent error occurs when students use circumference formulas for area problems or vice versa under time pressure. Test-takers who practice recognizing whether to leave answers in terms of pi or convert to decimals based on answer choice formats perform more efficiently on these sections.
What Are Circle Theorems About Inscribed Angles?
Circle theorems about inscribed angles establish relationships between angles formed by chords and the arcs they subtend. The angle in a semicircle theorem states that any angle inscribed in a semicircle (subtended by a diameter) measures exactly 90 degrees. The angles in the same segment theorem proves that all inscribed angles subtending the same arc are congruent. Students also learn that an inscribed angle measures half the central angle subtending the same arc, providing a powerful tool for solving complex geometric puzzles.
These theorems appear throughout engineering and design fields, particularly in CAD software and structural engineering where circular components require precise angle measurements. Architects use inscribed angle relationships when designing curved facades or circular windows to ensure structural supports meet at appropriate angles. Many students recognize the connection when examining bicycle wheels, where spokes radiating from a central hub create predictable angle relationships that engineers rely upon for balanced wheel construction.
How Can Teachers Use These Integrated Math 2 Circles Worksheets Effectively?
These worksheets support differentiated instruction by progressing from computational practice with pi to formal theorem proofs and three-dimensional applications. Teachers find that starting with concrete calculations builds confidence before introducing abstract proof structures. The answer keys allow students to self-check computational work during independent practice while teachers provide targeted feedback on proof reasoning. The variety of problem types helps identify whether struggles stem from arithmetic errors, conceptual misunderstandings about circle relationships, or difficulties with formal proof writing.
Many teachers use these worksheets for spiral review throughout the year, since circle concepts connect to coordinate geometry, trigonometry, and solid geometry topics appearing later in Integrated Math 2. The materials work well for test preparation stations where students rotate through computational fluency practice, theorem application, and proof construction. Teachers also assign specific worksheets for intervention when formative assessments reveal gaps in understanding pi calculations versus geometric reasoning about angle relationships within circles.