Integrated Math 2 Lines and Angles Worksheets
What Do Students Learn in Integrated Math 2 Lines and Angles?
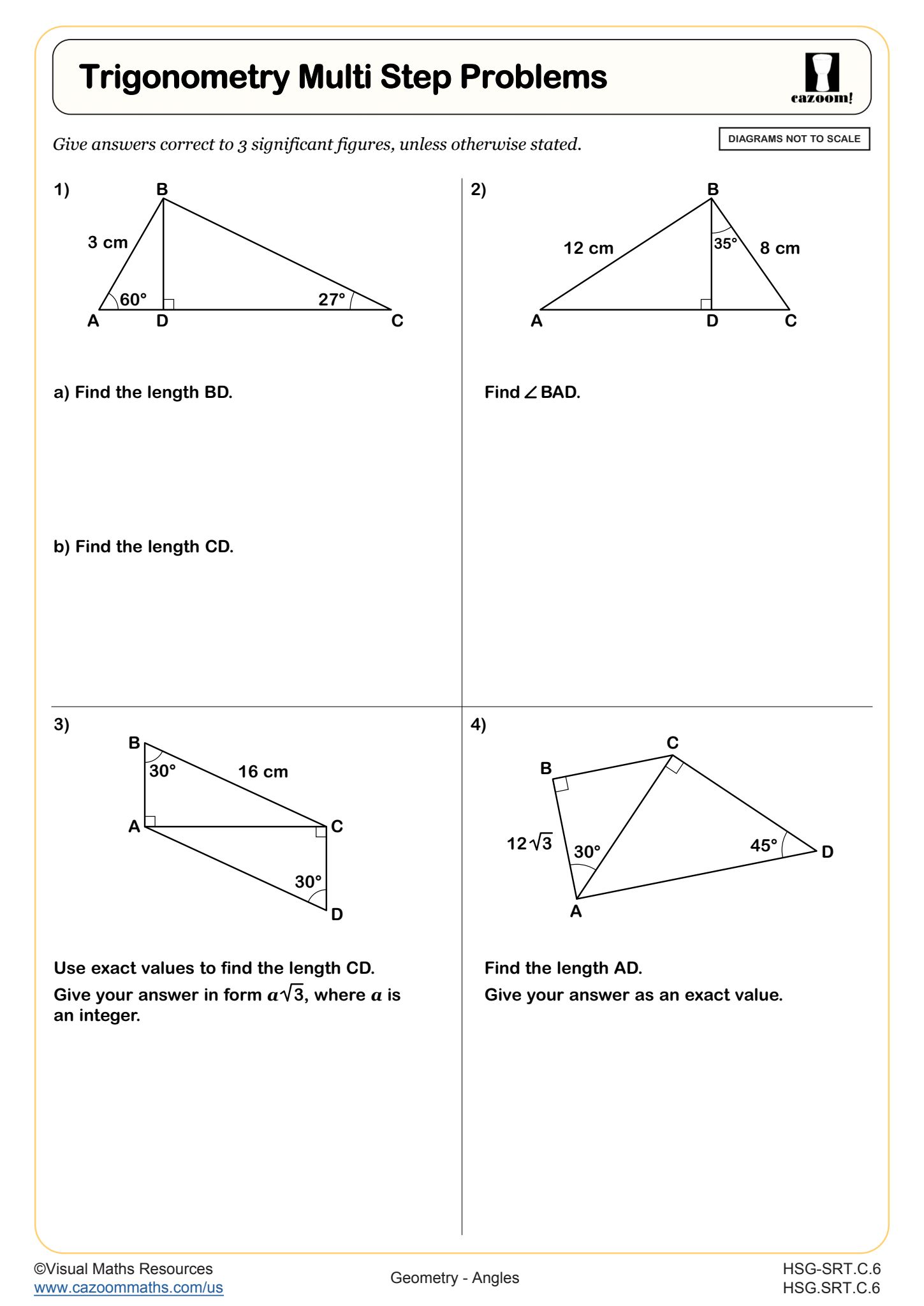
Integrated Math 2 students move beyond identifying angle types to applying trigonometric ratios in complex geometric contexts. This includes using the tangent ratio to find unknown side lengths or angle measures, solving problems that require multiple steps such as finding supplementary angles before calculating a ratio, and connecting angle relationships with right triangle trigonometry. The curriculum emphasizes problem-solving strategies that combine several concepts rather than isolated skill practice.
A common error emerges when students encounter problems where angles aren't already positioned in a right triangle—they often overlook the need to identify or construct a right triangle before applying trigonometric ratios. Students lose points when they correctly calculate tangent but fail to recognize which angle in the diagram corresponds to their calculation. Teachers notice breakthrough moments when students start drawing auxiliary lines to create right triangles within more complex figures.
How Are Lines and Angles Tested on the SAT and ACT?
Standardized tests embed lines and angles within multi-step geometry problems rather than asking direct questions about angle measures. The SAT frequently presents diagrams where students must recognize angle relationships (vertical, corresponding, or alternate interior angles) before applying trigonometric ratios to find lengths or areas. ACT problems often combine angle properties with coordinate geometry, requiring students to work with slopes as tangent ratios or calculate angles between lines.
Students lose points when they rush through the diagram analysis phase and miss critical angle relationships that unlock the problem. Another frequent mistake occurs when students correctly identify an angle measure but use the wrong trigonometric ratio because they misidentify the opposite and adjacent sides. Teachers preparing students for these assessments emphasize annotating diagrams with all known angle measures before attempting calculations, a habit that significantly improves accuracy under timed conditions.
What Is the Tangent Ratio and When Do Students Use It?
The tangent ratio relates an acute angle in a right triangle to the quotient of the opposite side length divided by the adjacent side length. Students use tangent to find unknown angles when two sides are known, or to calculate side lengths when one side and an angle are given. This ratio becomes particularly useful in multi-step problems where angle relationships must be established first—for example, finding a complement or supplement before determining which triangle sides to use in the tangent calculation.
Civil engineers and architects rely on tangent ratios when calculating slope grades for roads or determining roof pitch angles. Students encounter this application when analyzing accessibility ramps, which must meet specific angle requirements—a 4.8-degree angle corresponds to a 1:12 slope ratio, calculated using the tangent function. This connection helps students understand why trigonometry matters beyond classroom exercises and appears throughout STEM careers involving spatial reasoning and construction planning.
How Can Teachers Use These Worksheets in Integrated Math 2?
These worksheets provide structured practice that builds from applying single trigonometric ratios to solving multi-step problems requiring several geometric concepts. The tangent ratio problems and multi-step exercises include worked examples that model the problem-solving process, helping students see how to organize information from complex diagrams and determine which steps to perform first. Answer keys allow students to identify exactly where their reasoning breaks down—whether in setting up the ratio, performing calculations, or interpreting angle relationships.
Many teachers use these worksheets during review sessions before unit assessments, assigning specific problems that target common weaknesses identified in previous quizzes. The multi-step format works particularly well for paired work, where students verbalize their reasoning to partners and catch errors in logic before calculating. Teachers also find these useful for differentiated intervention, assigning scaffolded practice to students who need additional support with angle relationships while challenging advanced learners with the complete multi-step problems that mirror standardized test complexity.