Integrated Math 2 Transformations Worksheets
What transformation concepts do students practice in Integrated Math 2?
Integrated Math 2 students work with all four types of transformations: translations, reflections, rotations, and dilations. The curriculum emphasizes understanding which transformations preserve distance and angle measures (rigid motions) versus which change size but preserve shape (dilations). Students analyze how transformations affect coordinates, describe transformation sequences using precise mathematical language, and apply these concepts to prove figures are congruent or similar.
A common error occurs when students correctly perform a dilation but incorrectly assume it preserves congruence rather than creating similarity. Teachers frequently see students confuse the center of rotation with the center of dilation, especially when both appear in the same problem set. The worksheets address this by including problems where students must identify which properties remain invariant under specific transformations, building the conceptual foundation needed for formal geometric proofs later in the course.
How do standardized tests assess transformation skills?
The SAT and state assessments test transformations through multiple-choice and grid-in questions that require students to identify transformation types, determine coordinates after transformations, or recognize which sequence of transformations maps one figure onto another. Tests often embed transformation questions within similarity and congruence contexts, expecting students to justify why two figures are similar by describing the specific dilation and rigid motions connecting them. Many state assessments include technology-enhanced items where students drag figures or select transformation rules from dropdown menus.
Students lose points when they apply transformations in the wrong order within a sequence or fail to account for the center of dilation being somewhere other than the origin. Another frequent mistake occurs when students correctly identify that a dilation is involved but provide an incorrect scale factor because they measured from the wrong reference point. Questions involving reflections across lines other than the axes or rotations around points other than the origin prove particularly challenging under timed conditions.
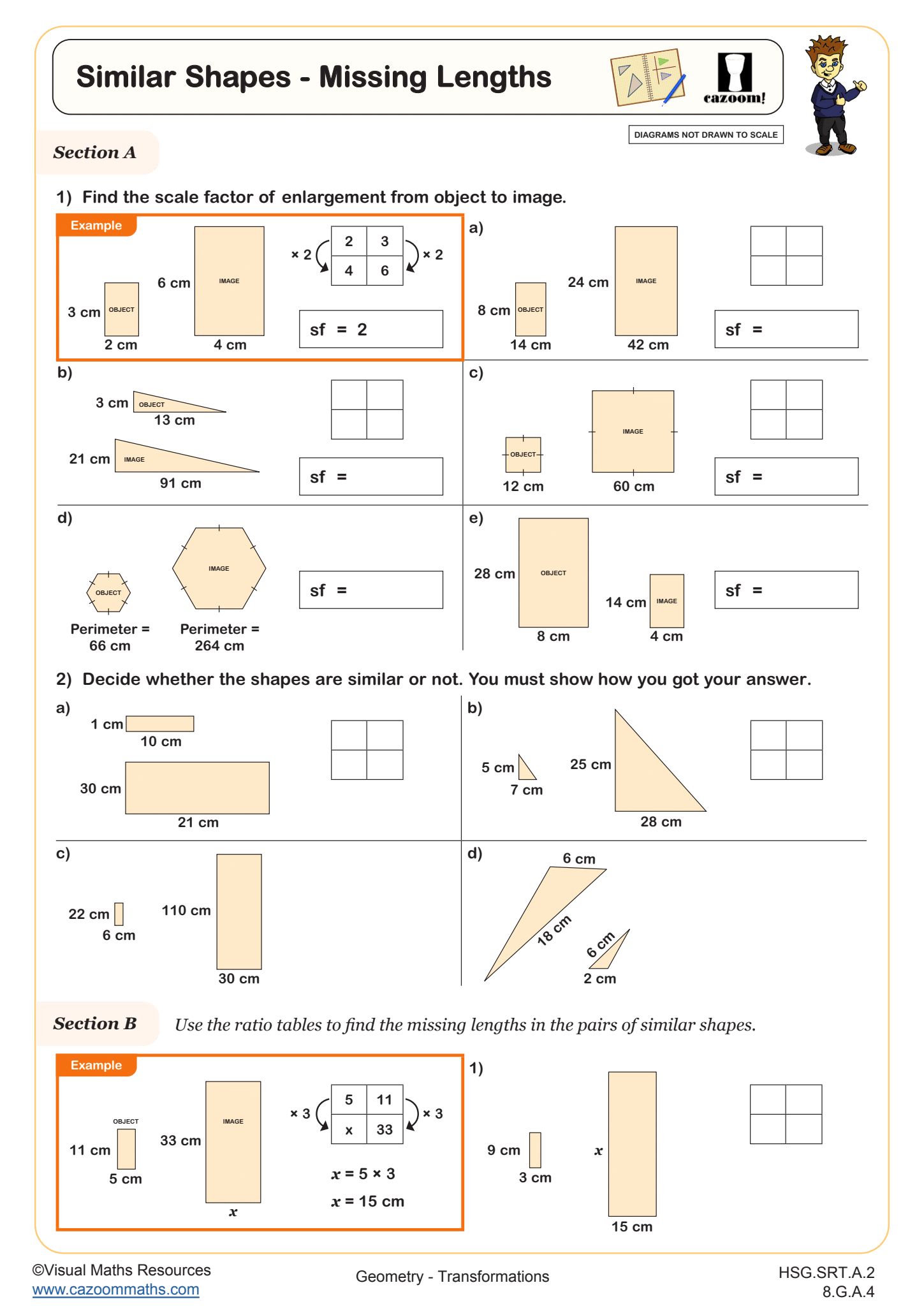
How do students determine missing lengths in similar shapes using transformations?
Students use the relationship between similar figures and dilations to find missing side lengths by identifying the scale factor connecting two shapes. When one figure is a dilation of another, corresponding sides are proportional, and the ratio between any pair of corresponding lengths equals the scale factor. Students set up proportions comparing known lengths to unknown lengths, then solve algebraically. This skill requires recognizing corresponding vertices and understanding that the scale factor applies consistently across all dimensions of the figure.
This concept connects directly to architecture and engineering, where scale drawings and models represent actual structures. Architects create blueprints where every measurement on paper relates to real-world dimensions through a consistent scale factor. Urban planners use similar figures when designing park layouts or city blocks that maintain proportional relationships. In manufacturing, quality control teams verify that produced parts match design specifications by checking that dimensions scale correctly, making this transformation skill applicable across multiple STEM careers.
How can teachers use these transformation worksheets effectively in Integrated Math 2?
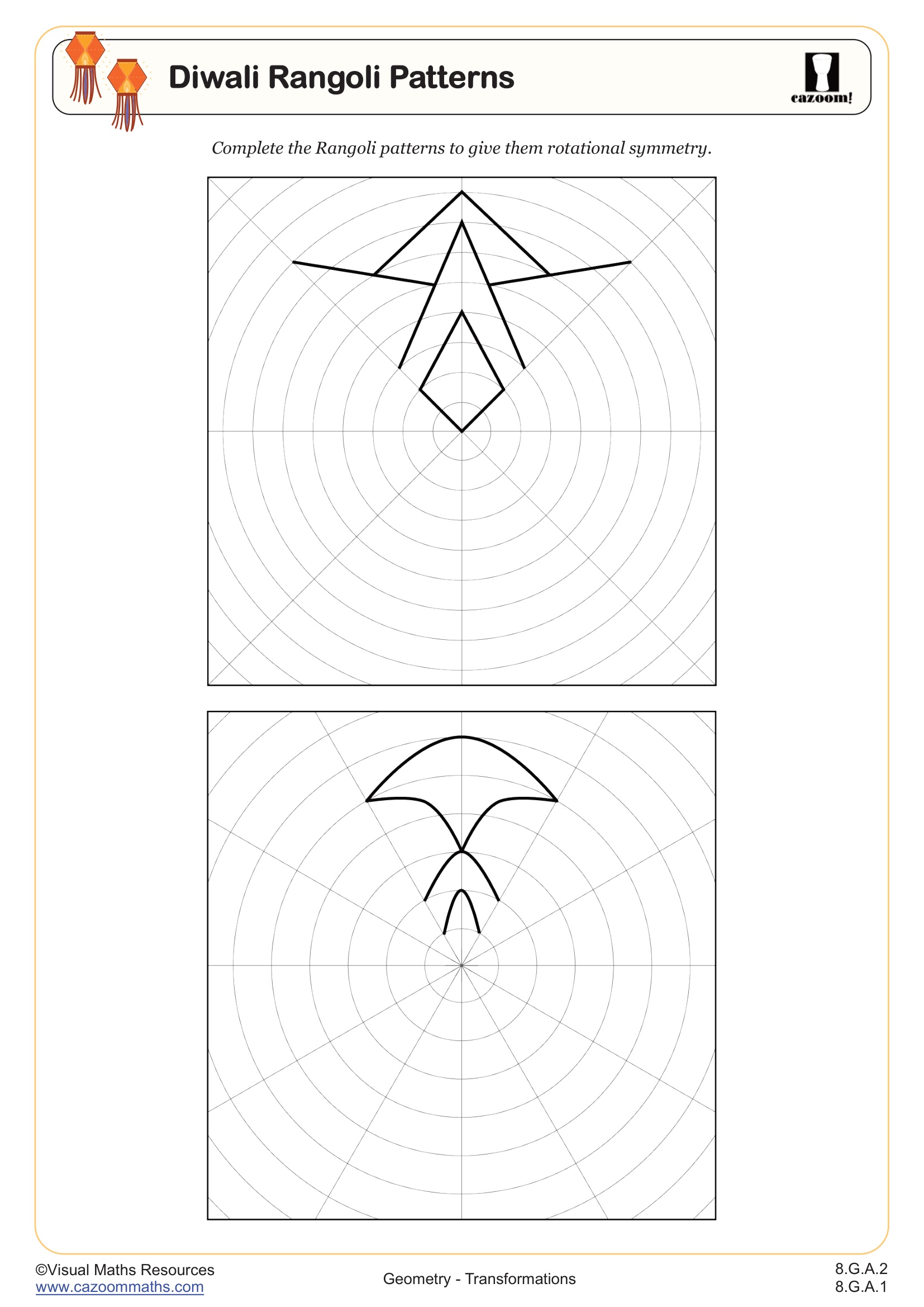
The worksheets provide structured practice that builds from identifying single transformations to analyzing complex sequences and applying transformations to similarity problems. The Rangoli patterns worksheet offers a culturally responsive approach to recognizing rotational and reflective symmetry, helping students visualize transformations in artistic contexts before formalizing rules. The similar shapes problems develop proportional reasoning by connecting the abstract concept of scale factor to concrete measurements students can calculate and verify.
Teachers use these worksheets as formative assessments before unit tests, assigning them after introducing transformation notation but before expecting mastery with composition of transformations. The answer keys allow for self-checking during partner work, where one student completes odd problems while another works evens, then they verify answers together and discuss discrepancies. The materials work well for intervention with students who performed poorly on transformation questions in previous assessments, providing focused review without overwhelming them with excessive problem sets.