Integrated Math 2 Trigonometry Worksheets
What Trigonometry Concepts Are Covered in Integrated Math 2?
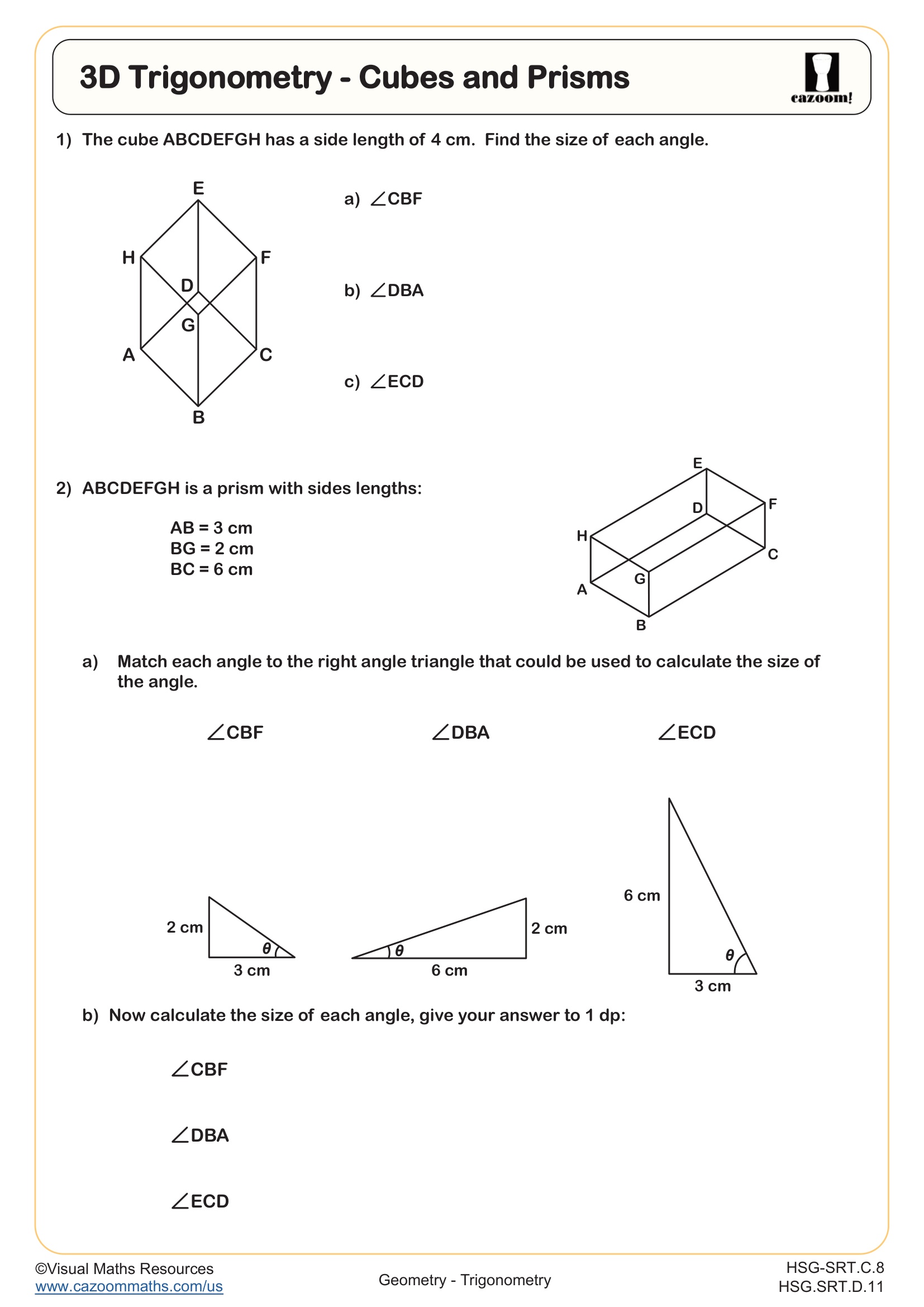
Integrated Math 2 trigonometry focuses on right triangle trigonometry as a problem-solving tool, emphasizing when and how to apply sine, cosine, and tangent ratios. Students learn to distinguish situations requiring the Pythagorean Theorem from those needing trigonometric ratios, select appropriate trigonometric rules for given information, solve multi-step problems involving angles of elevation and depression, and extend two-dimensional reasoning to three-dimensional contexts like finding diagonal lengths in rectangular prisms or angles in pyramids.
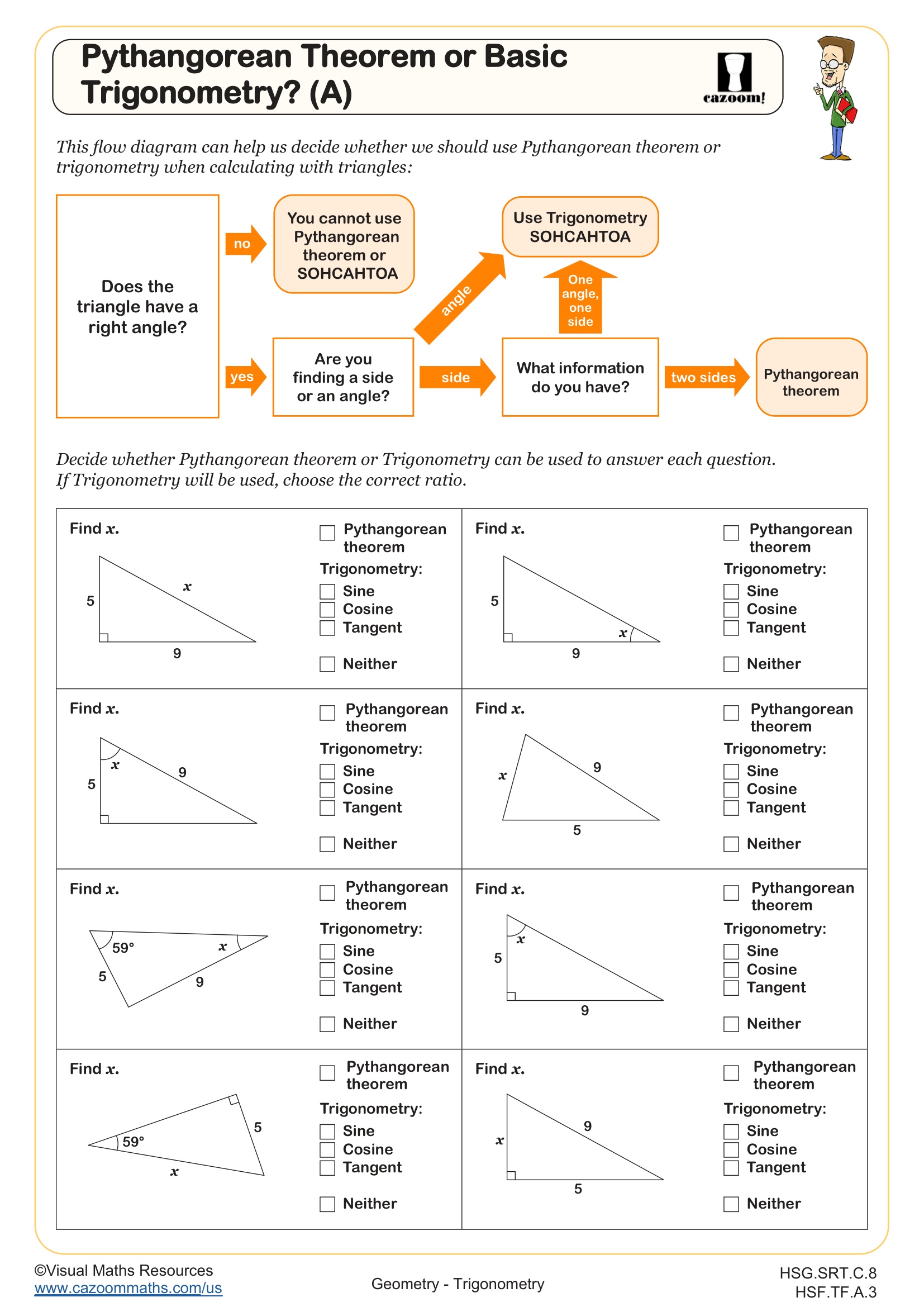
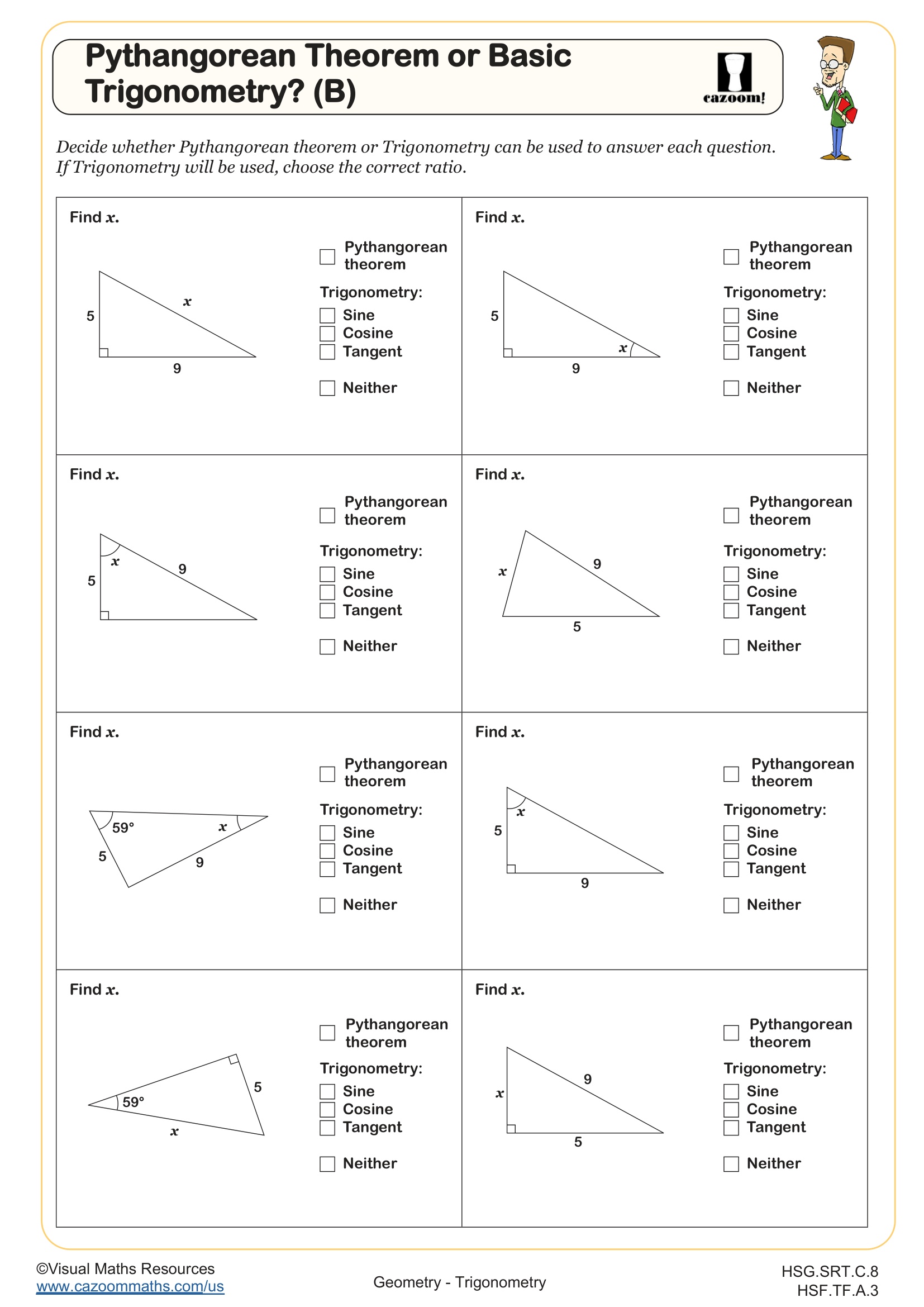
A common error occurs when students attempt to use trigonometric ratios with three side lengths but no angle measure, or conversely, try applying the Pythagorean Theorem when only one side and one angle are known. Teachers see breakthrough moments when students create decision trees or flowcharts that guide their choice between Pythagorean versus trigonometric approaches based on the given information in each problem.
How Does Trigonometry Appear on the SAT and ACT?
Standardized tests like the SAT and ACT include right triangle trigonometry in both calculator and no-calculator sections, typically presenting problems embedded in real-world contexts such as ramps, ladder placement, or sight lines. Students must recognize trigonometric relationships within diagrams, set up correct ratios or equations, and solve for missing measurements. The ACT specifically tests knowledge of basic trigonometric values for common angles like 30°, 45°, and 60°, while both tests expect fluency in choosing the correct trigonometric ratio based on which sides and angles are involved.
Students lose points when they confuse which ratio to use, particularly mixing up opposite and adjacent sides relative to the reference angle. Another frequent assessment error involves setting up the equation correctly but making calculation mistakes with inverse trigonometric functions on calculators, especially when answers need rounding to specific decimal places. Test questions deliberately include answer choices reflecting these common setup and calculation errors.
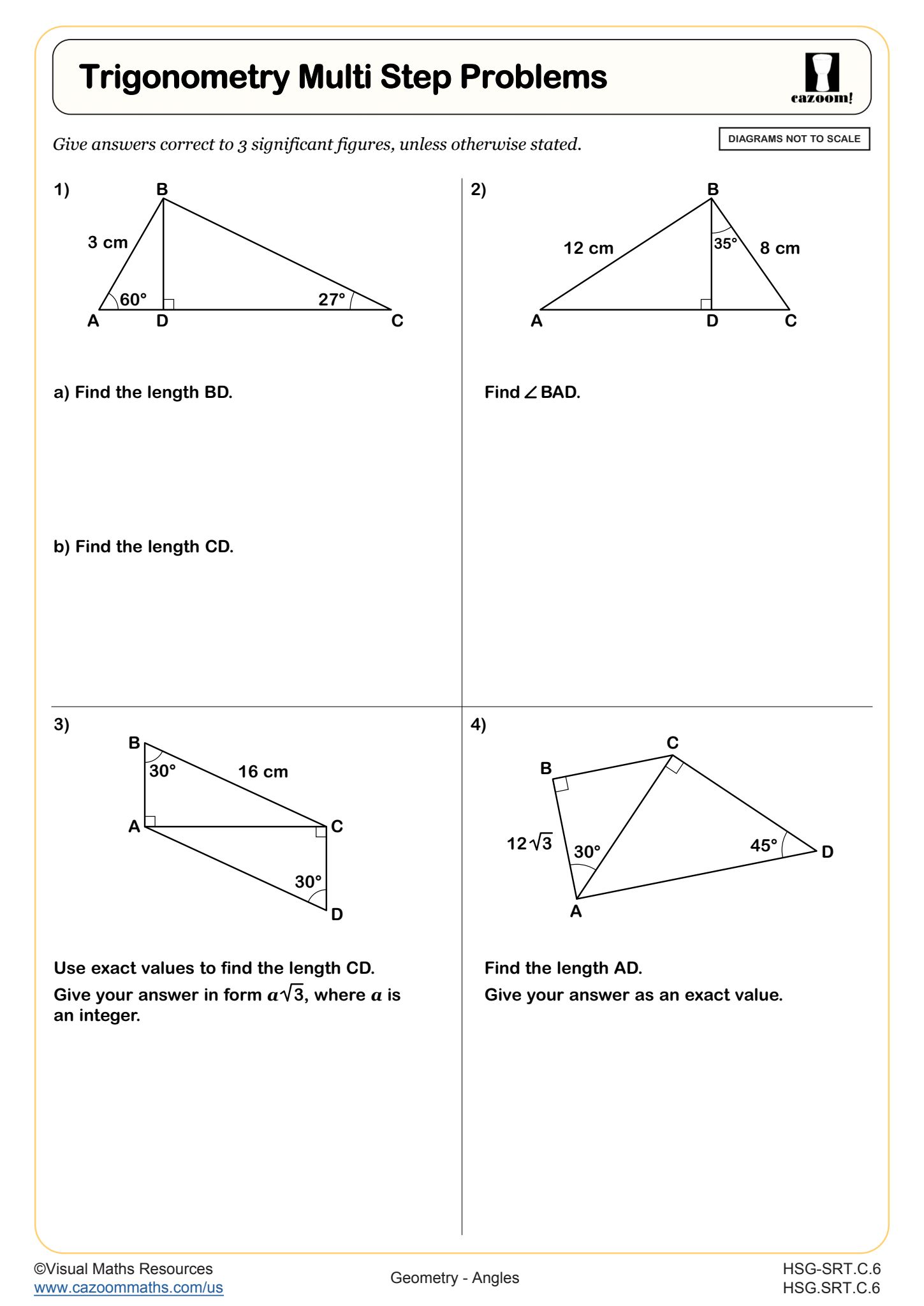
What Are Multi-Step Trigonometry Problems?
Multi-step trigonometry problems require students to find one measurement before they can determine the final answer, building problem-solving stamina and strategic thinking. For example, students might first use tangent to find the height of a building from an angle of elevation, then use that height with a different angle to find a second distance. These problems assess whether students can identify the logical sequence of calculations needed and maintain accuracy across multiple steps while tracking which values are known versus unknown at each stage.
This skill connects directly to STEM fields where professionals solve complex spatial problems by breaking them into manageable parts. Surveyors use multi-step trigonometric calculations to map property boundaries across varied terrain, while architects determine optimal roof angles by first calculating structural heights. Engineers designing wheelchair ramps must calculate horizontal run distances from required angles and vertical rises, demonstrating how trigonometric problem-solving appears throughout technical careers.
How Can Teachers Use These Trigonometry Worksheets in Integrated Math 2?
These worksheets provide scaffolded practice that moves students from identifying which mathematical tool to use through solving increasingly complex problems. The worksheets distinguishing Pythagorean Theorem from trigonometry build critical decision-making skills before students tackle multi-step and three-dimensional applications. Teachers find that having students explain their reasoning for choosing a particular approach, either in writing or to a partner, strengthens conceptual understanding beyond procedural execution. The complete answer keys allow students to check their work independently and identify exactly where errors occurred in their solution process.
Many teachers use these worksheets for differentiated instruction during unit reviews or as targeted intervention for students who struggle on formative assessments. The progression from choosing the correct rule through three-dimensional applications works well for station rotations or individualized practice plans. Teachers also assign specific worksheets as SAT or state assessment preparation since the problem types mirror standardized test formats. Paired work on multi-step problems encourages mathematical discourse as students justify their solution strategies to each other.