Integrated Math 3 Circles Worksheets
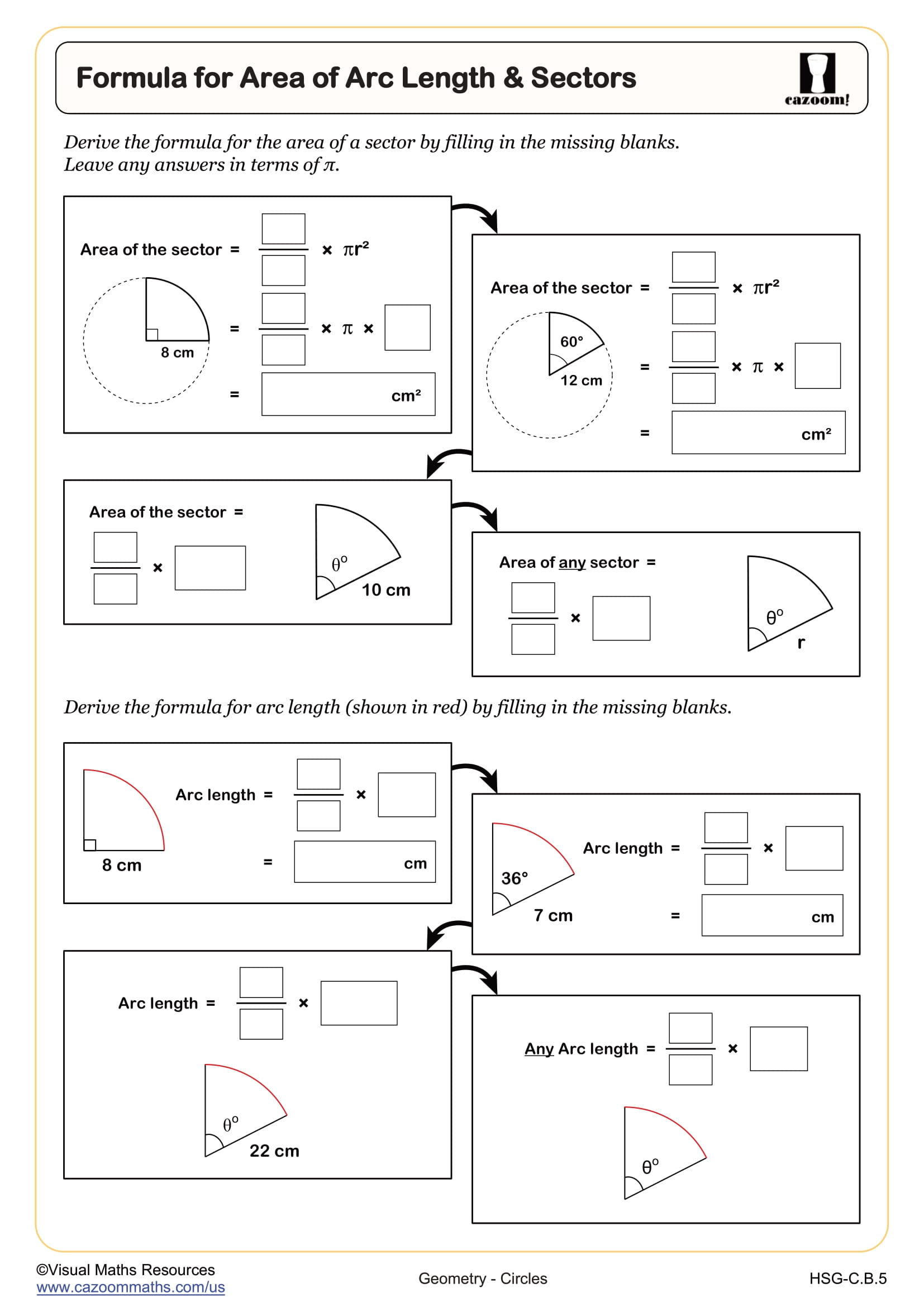
Area of Arc Lengths & Sectors

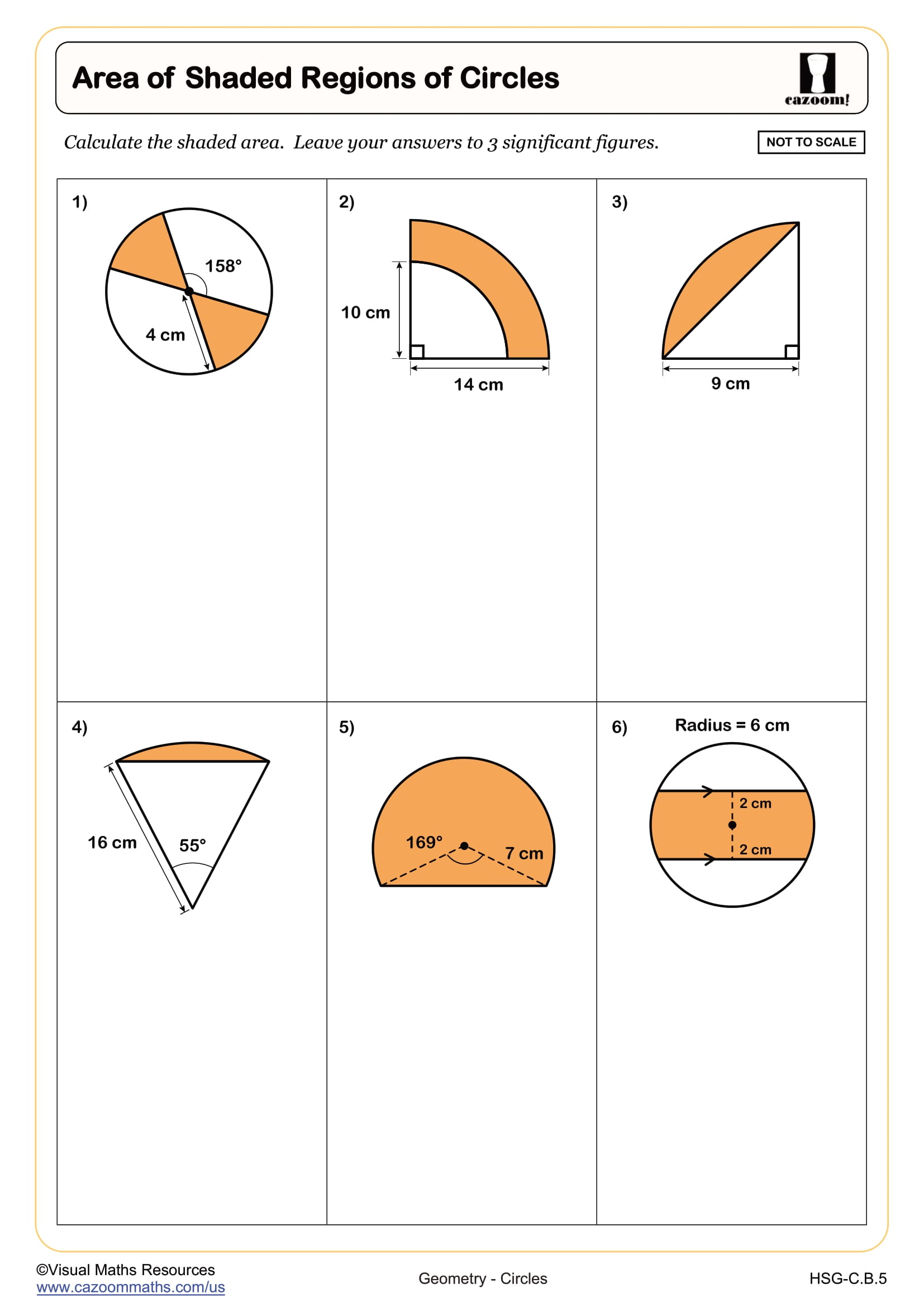
Area of Shaded Regions of Circles
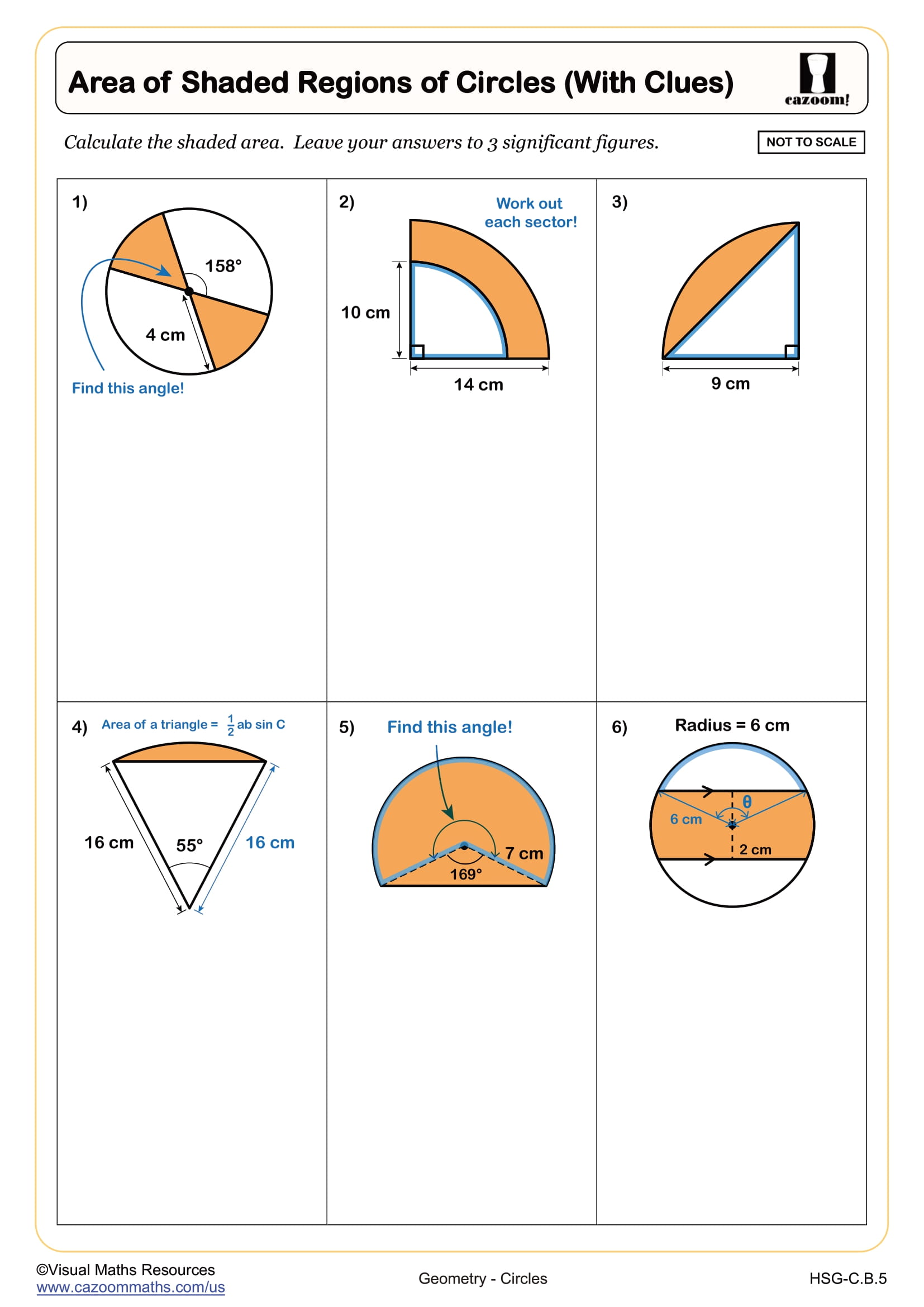
Area of Shaded Regions of Circles (with clues)
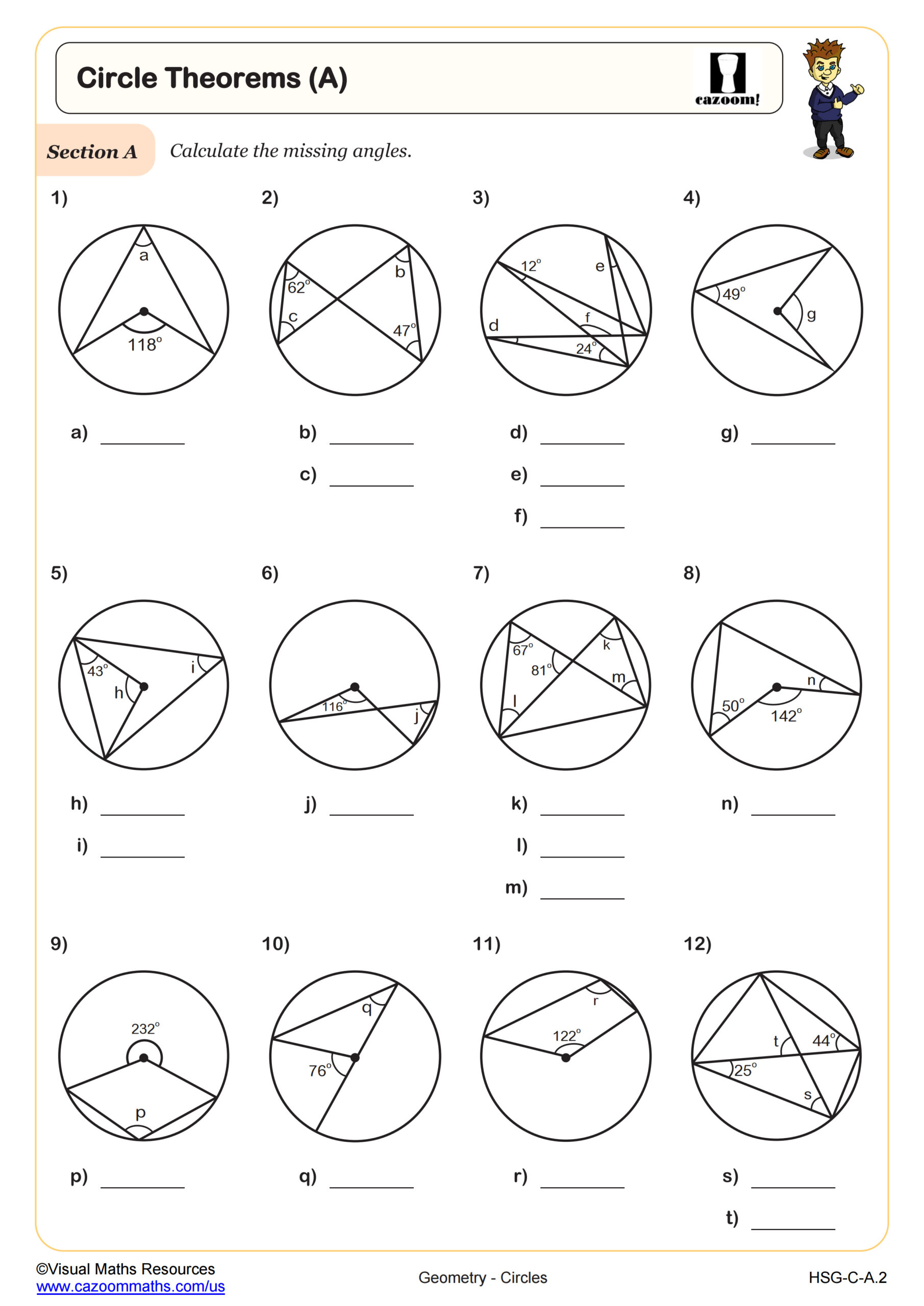
Circle Theorems (A)
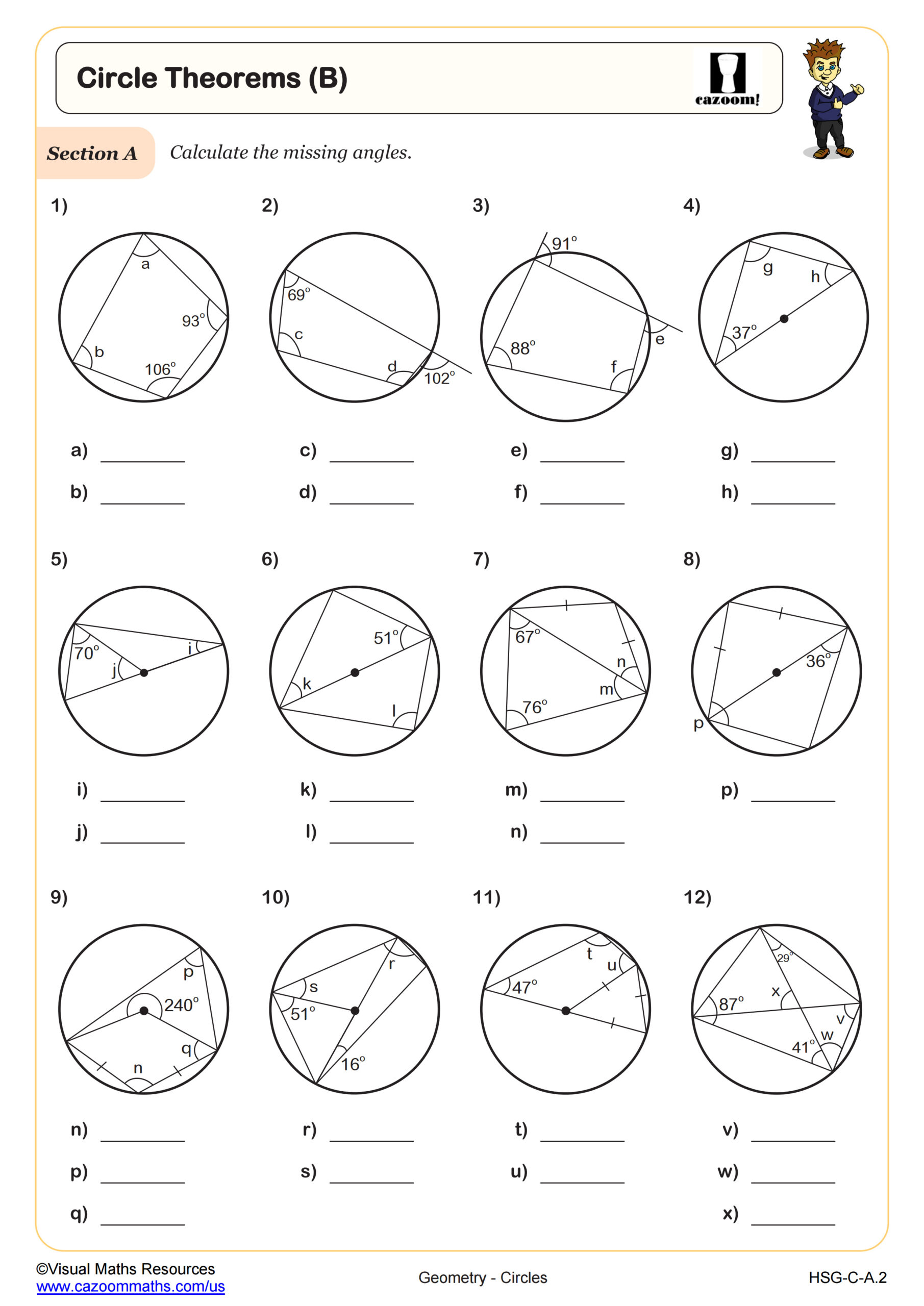
Circle Theorems (B)
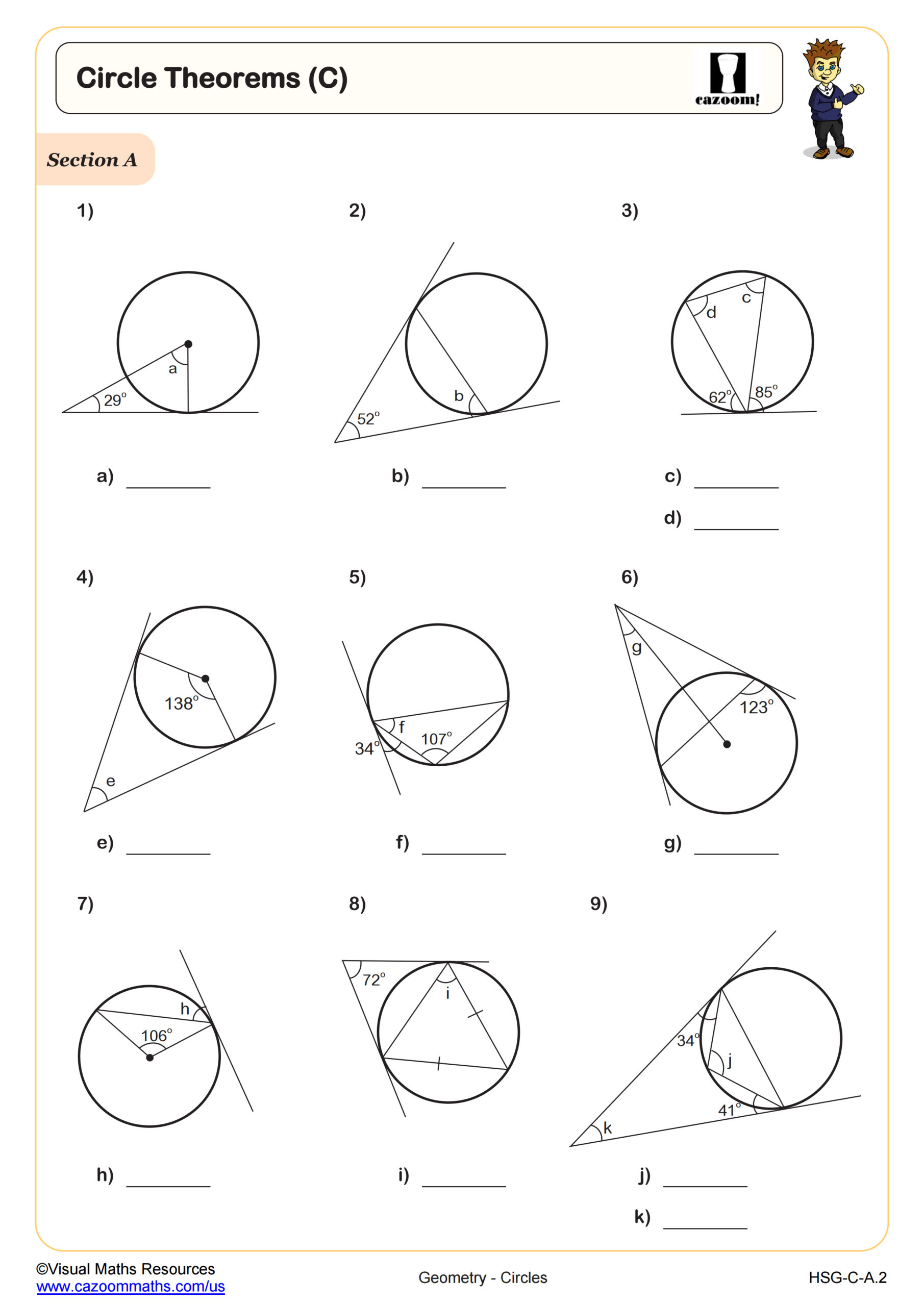
Circle Theorems (C)
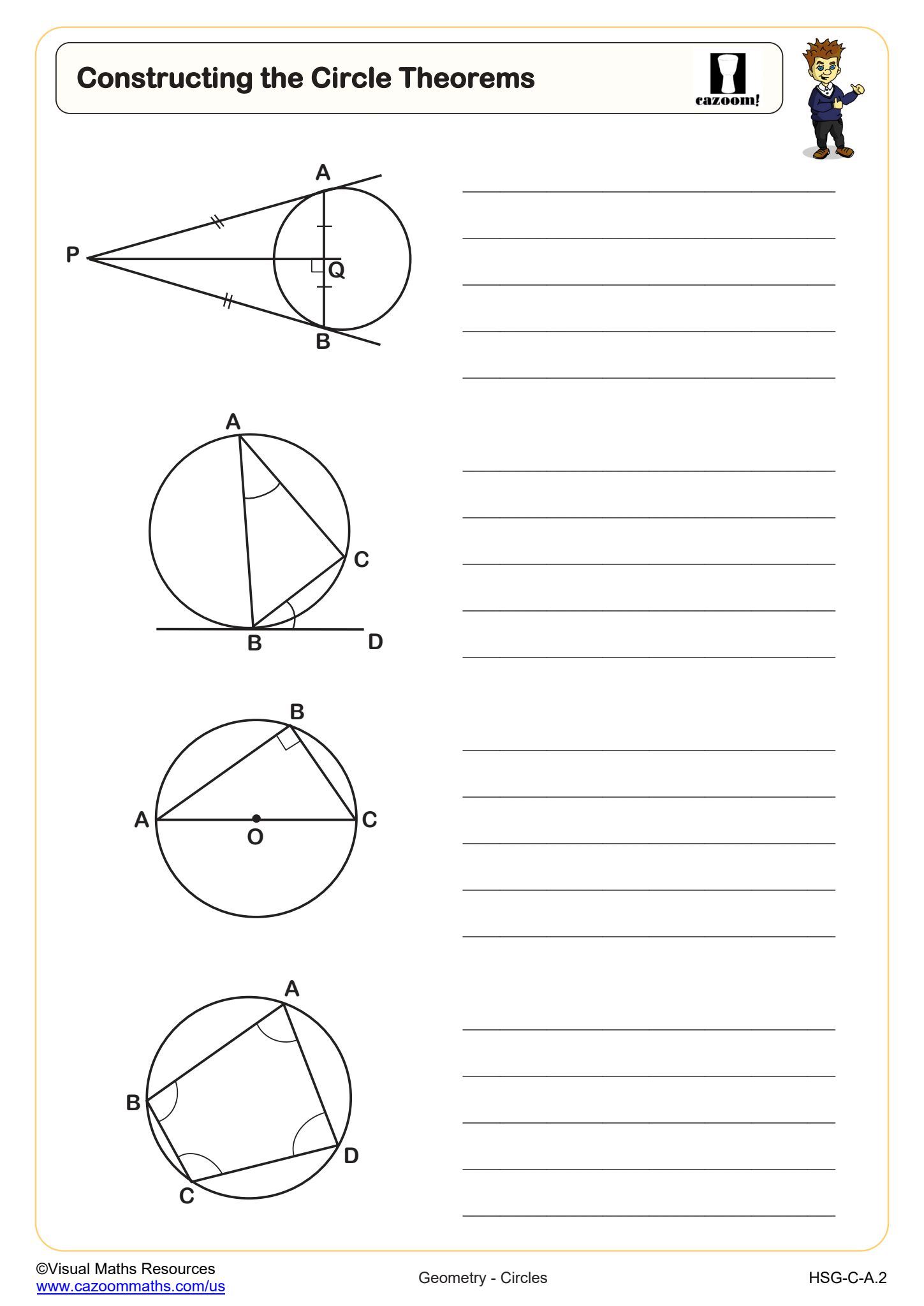
Constructing the Circle Theorems
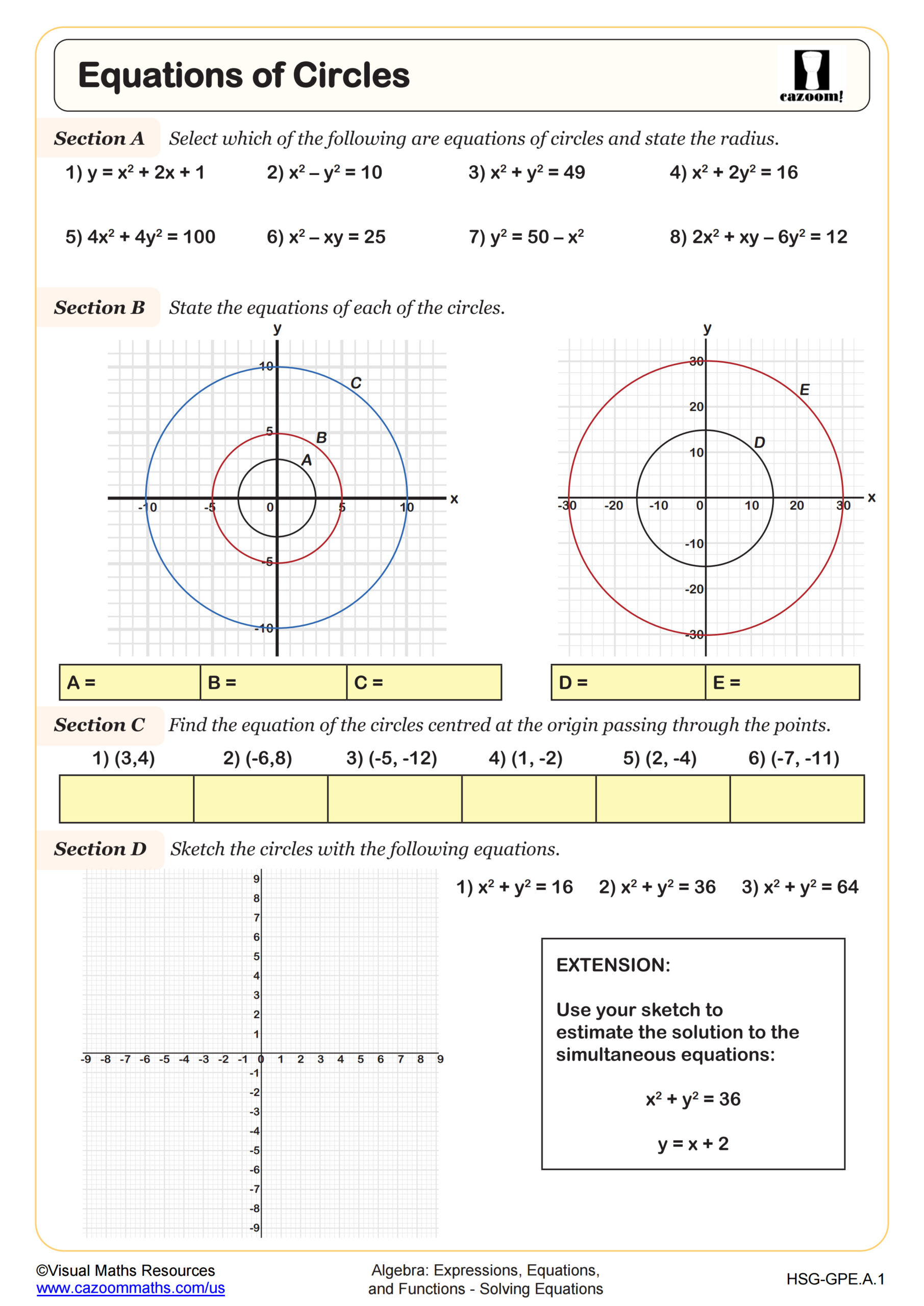
Equations of Circles
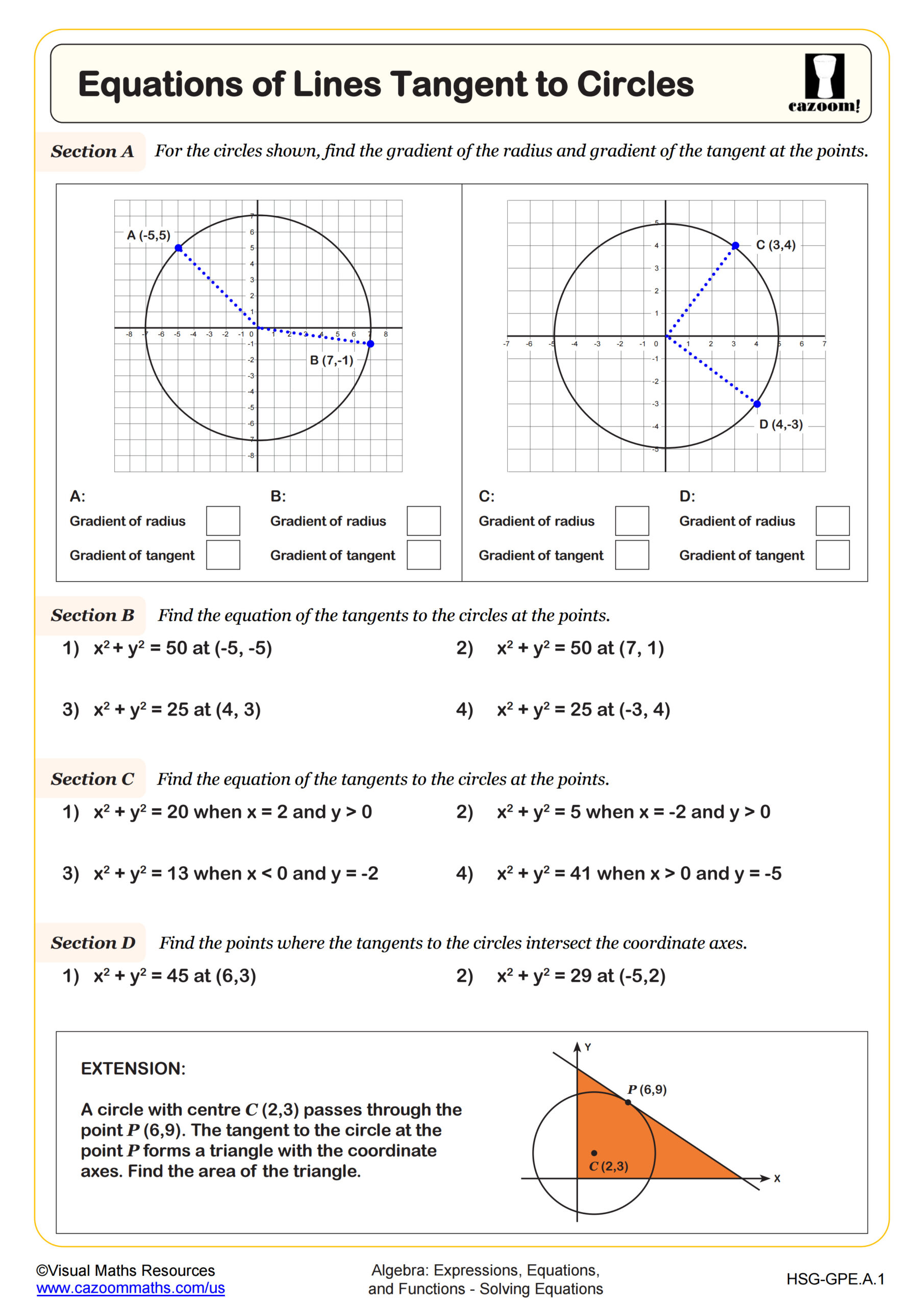
Equations of Lines Tangent to Circles
Formula for Area of Arc Length & Sectors
Introducing Radians

What Circle Concepts Do Integrated Math 3 Students Need to Master?
Integrated Math 3 circles topics extend beyond basic circumference and area formulas to include radian measure, inscribed and central angle theorems, tangent-secant relationships, and equations of circles in coordinate geometry. Students work with the standard form (x-h)²+(y-k)²=r² and general form of circle equations, converting between forms and determining tangent line equations at specific points.
A common error occurs when students apply degree-based reasoning to radian problems, particularly when converting arc length to angle measure. Teachers notice that students often forget that radians represent the ratio of arc length to radius, leading to mistakes when they try to "convert" radians the same way they convert between different unit systems. Worksheets that explicitly contrast degree and radian reasoning help students recognize these fundamental differences.
How Are Circle Concepts Tested on the SAT and ACT?
Standardized tests like the SAT and ACT regularly assess circle theorems through coordinate geometry problems, often combining circle equations with linear equations to test tangent relationships or intersection points. Students must demonstrate fluency with completing the square to rewrite circle equations, calculating arc lengths and sector areas, and applying inscribed angle theorems to find unknown measures in diagrams.
Students lose points when they misidentify the center or radius from general form equations without first converting to standard form. Another frequent mistake involves applying the inscribed angle theorem backward, assuming the central angle equals twice the inscribed angle regardless of which angle is given. Timed practice with these specific question types builds the pattern recognition needed for test success.
Why Is Understanding Radian Measure Important Beyond Geometry?
Radian measure provides the foundation for all higher mathematics, particularly calculus and physics. Unlike degrees, which are arbitrary divisions of a circle, radians represent a natural ratio that simplifies derivative and integral formulas for trigonometric functions. Students who master radian thinking in Integrated Math 3 transition more smoothly into Pre-Calculus and Calculus, where degree measures rarely appear.
Engineers and physicists use radians exclusively when calculating angular velocity, rotational motion, and wave functions. A wheel rotating at 500 revolutions per minute translates to angular velocity in radians per second, which then connects directly to linear velocity through the relationship v=rω. College-bound STEM students benefit significantly from developing radian fluency now rather than struggling with notation changes later in technical coursework.
How Can Teachers Use These Circles Worksheets in Integrated Math 3?
These worksheets build understanding through strategic sequencing, starting with visual construction activities that develop intuition about angle relationships before moving to formal theorem applications and algebraic representations. The progression from circle theorems to tangent line equations mirrors how coordinate geometry and pure geometry intersect in Integrated Math 3. Answer keys enable students to check their reasoning on multi-step problems independently.
Many teachers use the construction-based worksheets during initial instruction to help students discover relationships before formal proofs, then assign theorem application sheets for homework practice. The tangent line equation worksheets work particularly well for test preparation since they combine multiple skills: completing the square, finding slopes of perpendicular lines, and writing linear equations. Pairing students on proof-based problems encourages mathematical discourse about valid reasoning steps, while radian conversion sheets provide targeted intervention for students who need additional practice with this foundational concept.