Integrated Math 3 Functions Worksheets
What Function Skills Do Students Practice in Integrated Math 3?
Integrated Math 3 functions worksheets focus on inverse and composite functions, extending the foundational function concepts from earlier integrated math courses. Students work with finding inverse functions algebraically and graphically, verifying inverse relationships, and composing two or more functions to create new relationships. These skills align with Common Core standards for understanding function operations and preparing students for advanced mathematical modeling.
Teachers frequently observe that students confuse the notation for inverse functions (f⁻¹) with reciprocal functions (1/f), leading to calculation errors. Worksheets that clearly distinguish between these notations and provide repeated practice with both help students develop accuracy. Many teachers find that having students verify inverse pairs by composition eliminates this confusion more effectively than explanation alone.
How Do Function Concepts Appear on the SAT and ACT?
Standardized tests like the SAT and ACT regularly include questions about composite functions and inverse functions, often embedded within word problems or multi-step reasoning tasks. Students must evaluate composite functions like f(g(3)), determine domain restrictions after composition, and recognize inverse relationships from tables or graphs. The ACT tends to present these concepts within coordinate geometry contexts, while the SAT frequently combines function composition with algebraic manipulation.
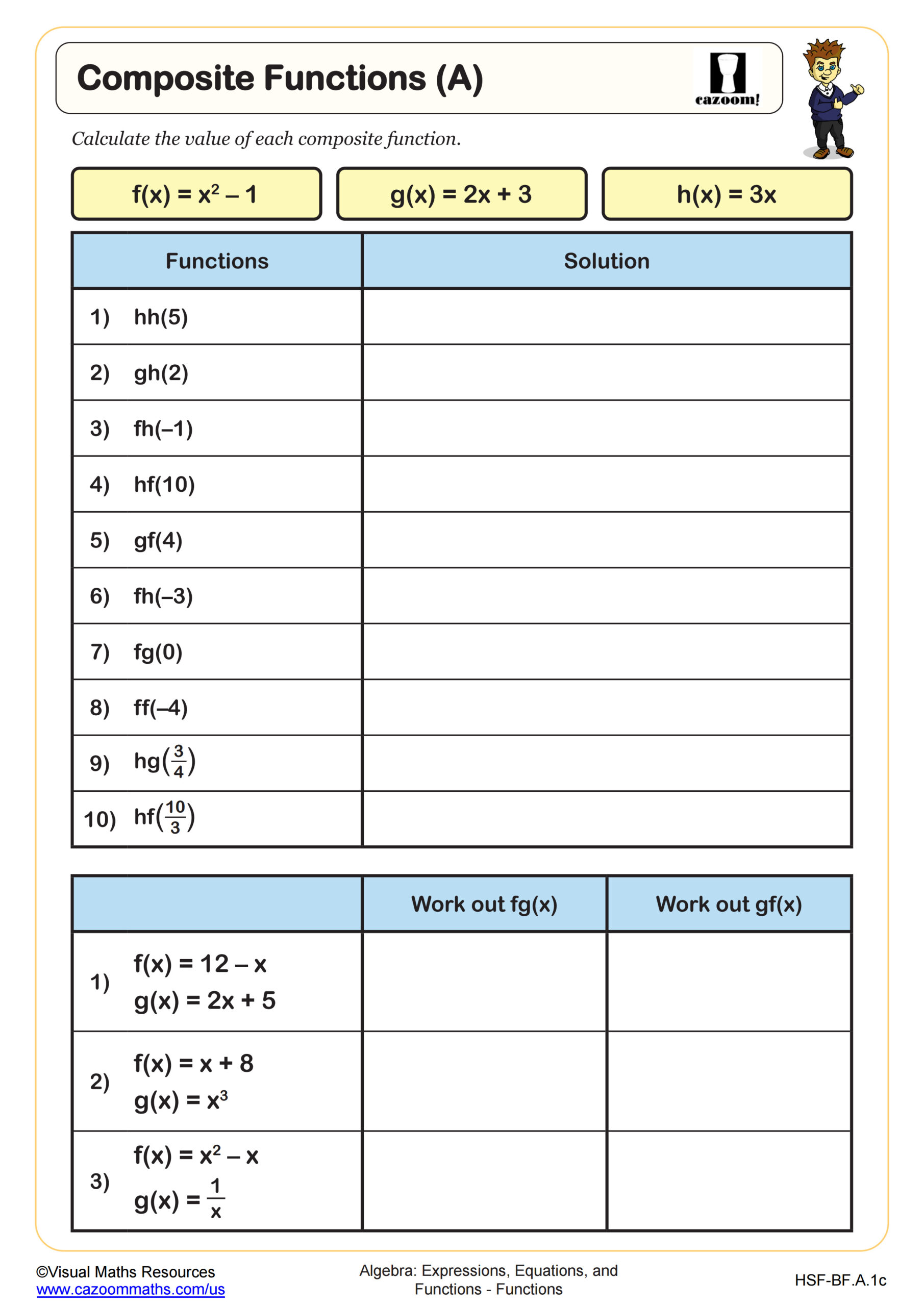
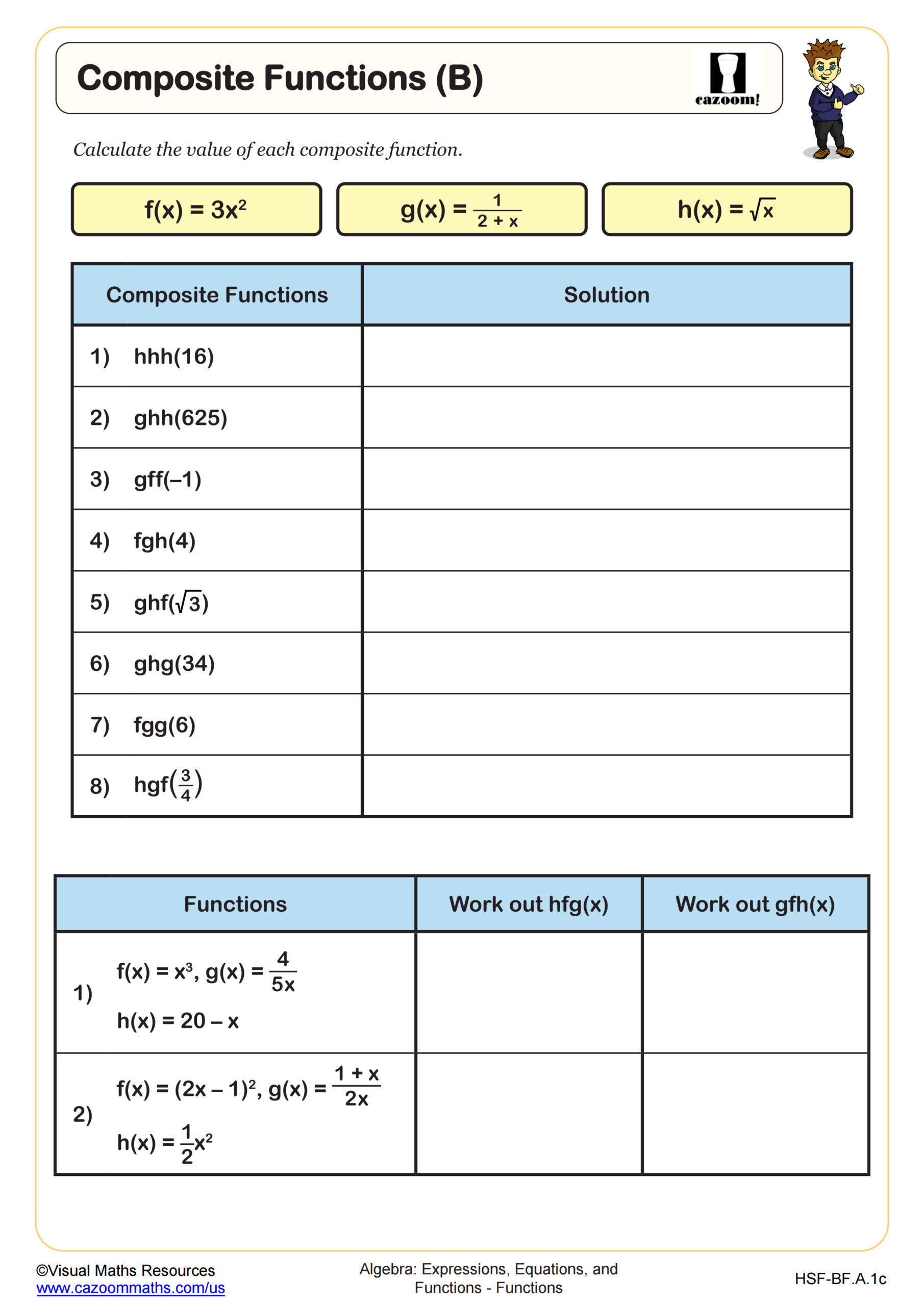
Students lose points when they fail to follow the correct order for composite functions, evaluating f(g(x)) as g(f(x)) instead. Another common error involves assuming all functions have inverses without checking whether the original function is one-to-one. Teachers notice that students who practice verifying inverse relationships through composition perform significantly better on assessment questions requiring multi-step function reasoning.
What Makes Composite Functions Challenging for Students?
Composite functions require students to evaluate functions within functions, following a specific inside-out order that contradicts the left-to-right reading students use elsewhere. For f(g(x)), students must evaluate g(x) first, then substitute that result into f. This reversal of intuitive order causes confusion until students develop systematic habits. Teachers observe that notation like (f ∘ g)(x) initially helps some students visualize the process, while others benefit from color-coding the evaluation steps.
Composite functions appear throughout STEM fields, particularly in physics and engineering where transformations build upon each other. For example, converting temperature from Celsius to Kelvin, then from Kelvin to energy calculations, involves function composition. College-bound students encounter composite functions extensively in calculus when working with the chain rule, making this high school foundation directly transferable to higher mathematics and applied science coursework.
How Can Teachers Use These Functions Worksheets in Integrated Math 3?
These worksheets provide structured practice with inverse and composite functions through problems that increase in complexity, allowing students to build confidence with notation before tackling multi-step applications. The answer keys enable students to self-check their work during independent practice, helping them identify whether errors stem from notation confusion or computational mistakes. Teachers find that worksheets labeled A and B provide flexibility for differentiation or for creating parallel assessments.
Many teachers assign these worksheets as targeted homework after introducing inverse or composite functions, then use the answer keys for quick classroom review of common mistakes. The worksheets work well for test preparation before state assessments or semester exams, as they isolate function operations that students must perform quickly and accurately under timed conditions. Paired work where students compare their solution processes often reveals conceptual gaps that whole-class instruction misses.