Integrated Math 3 Trigonometry Worksheets
Describing Transformations of Trigonometric Functions

Graphs of Trigonometric Functions (A)
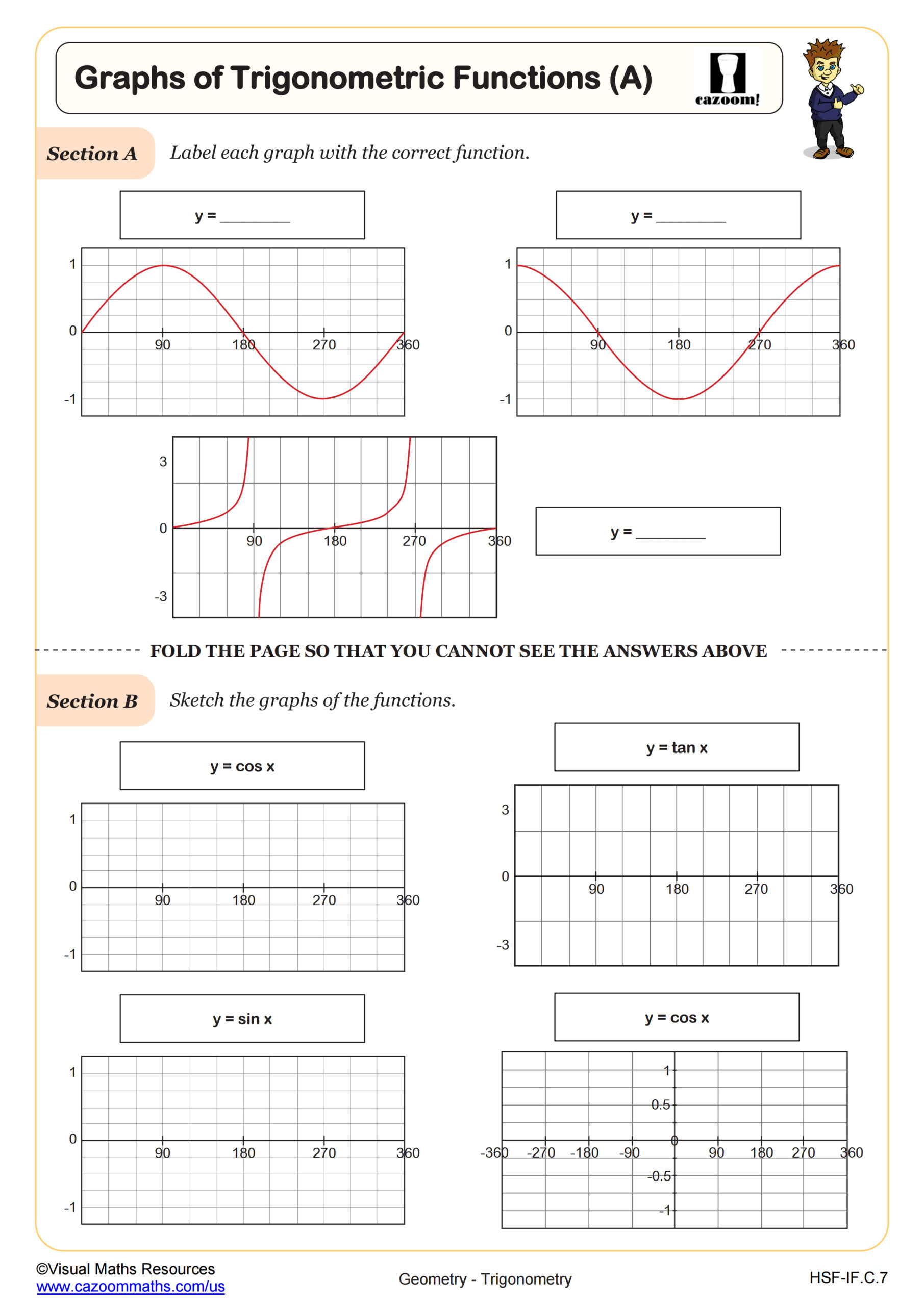
Graphs of Trigonometric Functions (B)

Solving Trigonometric Equations

The Cosine Rule - Finding Angles
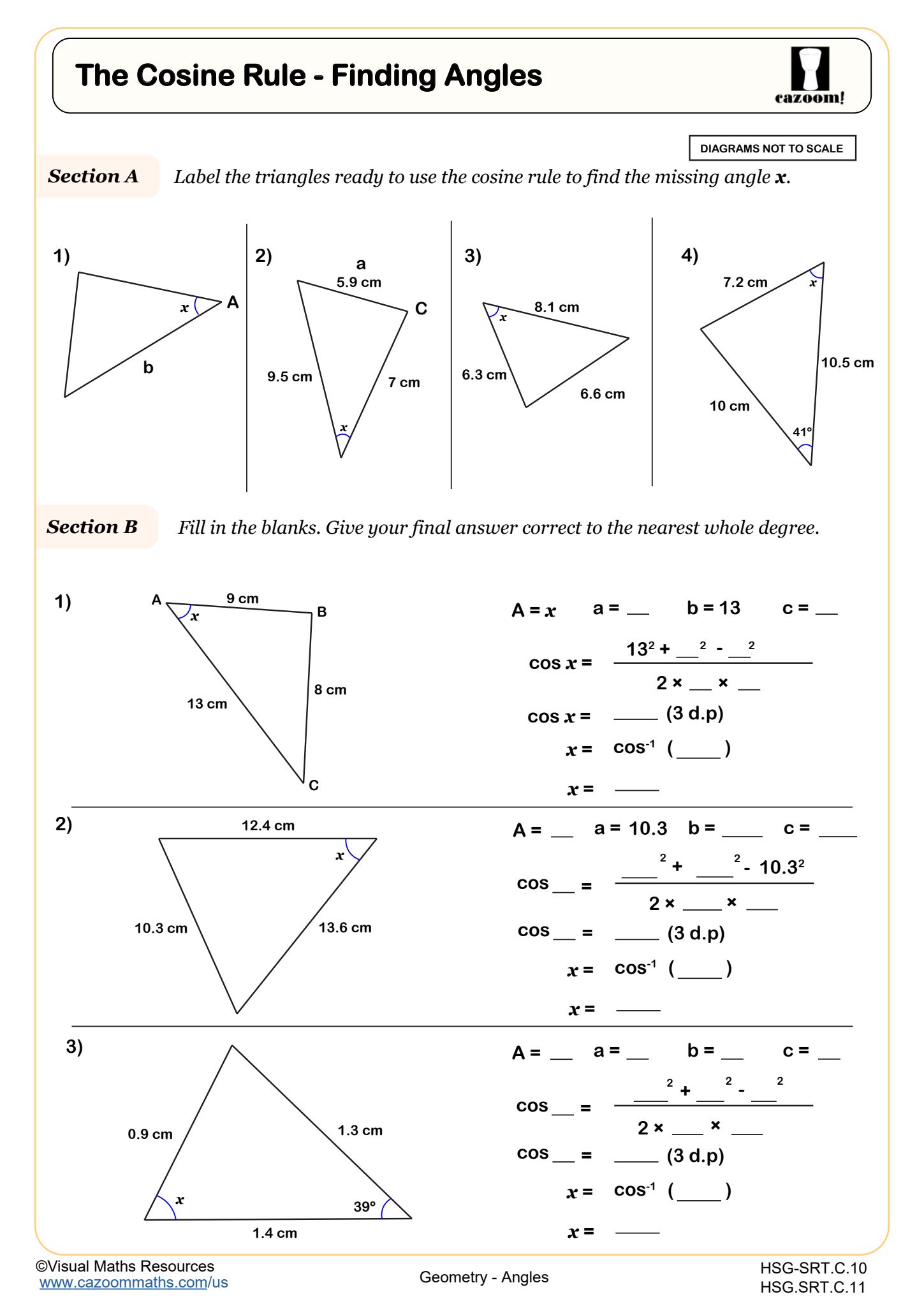
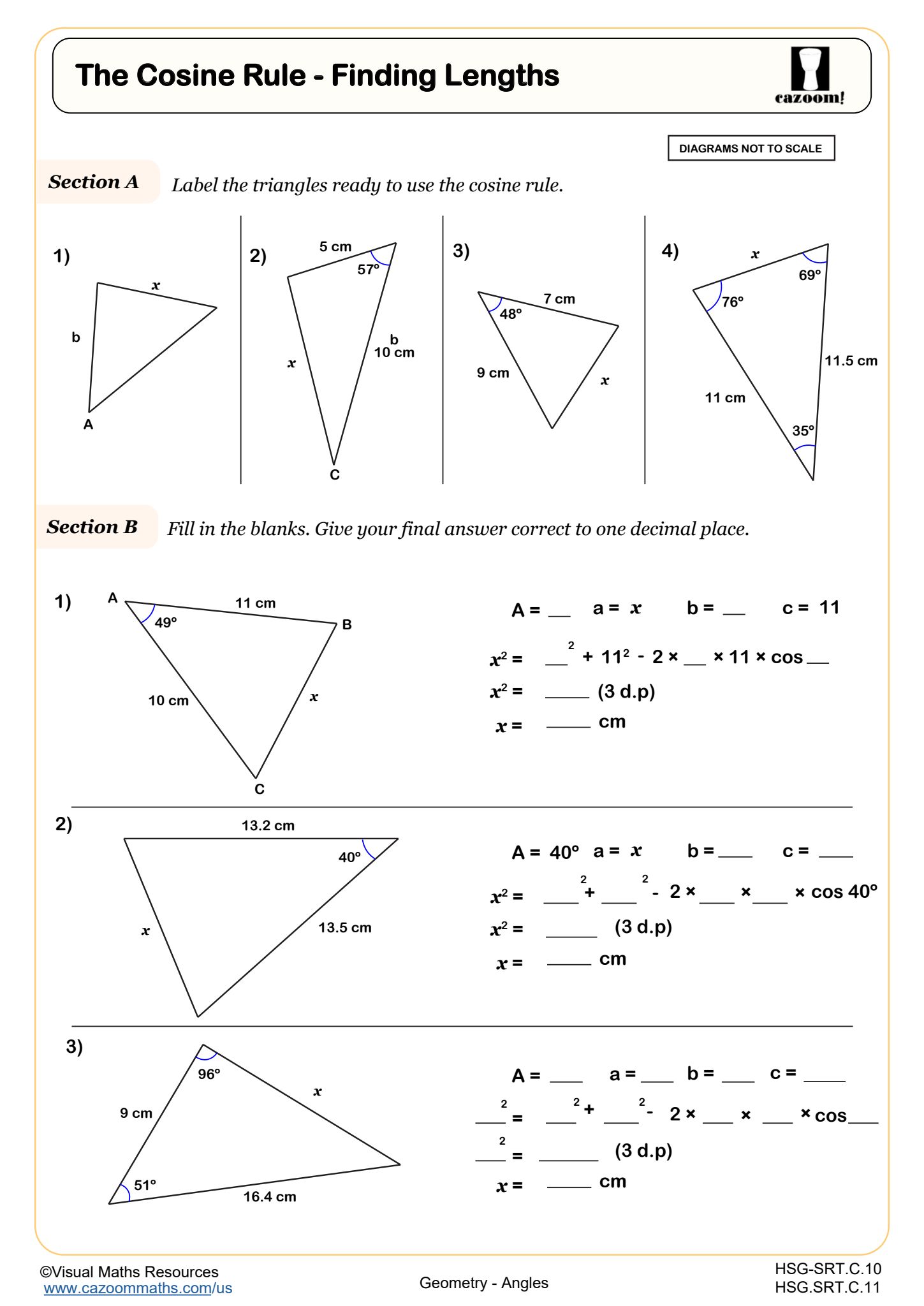
The Cosine Rule - Finding Lengths
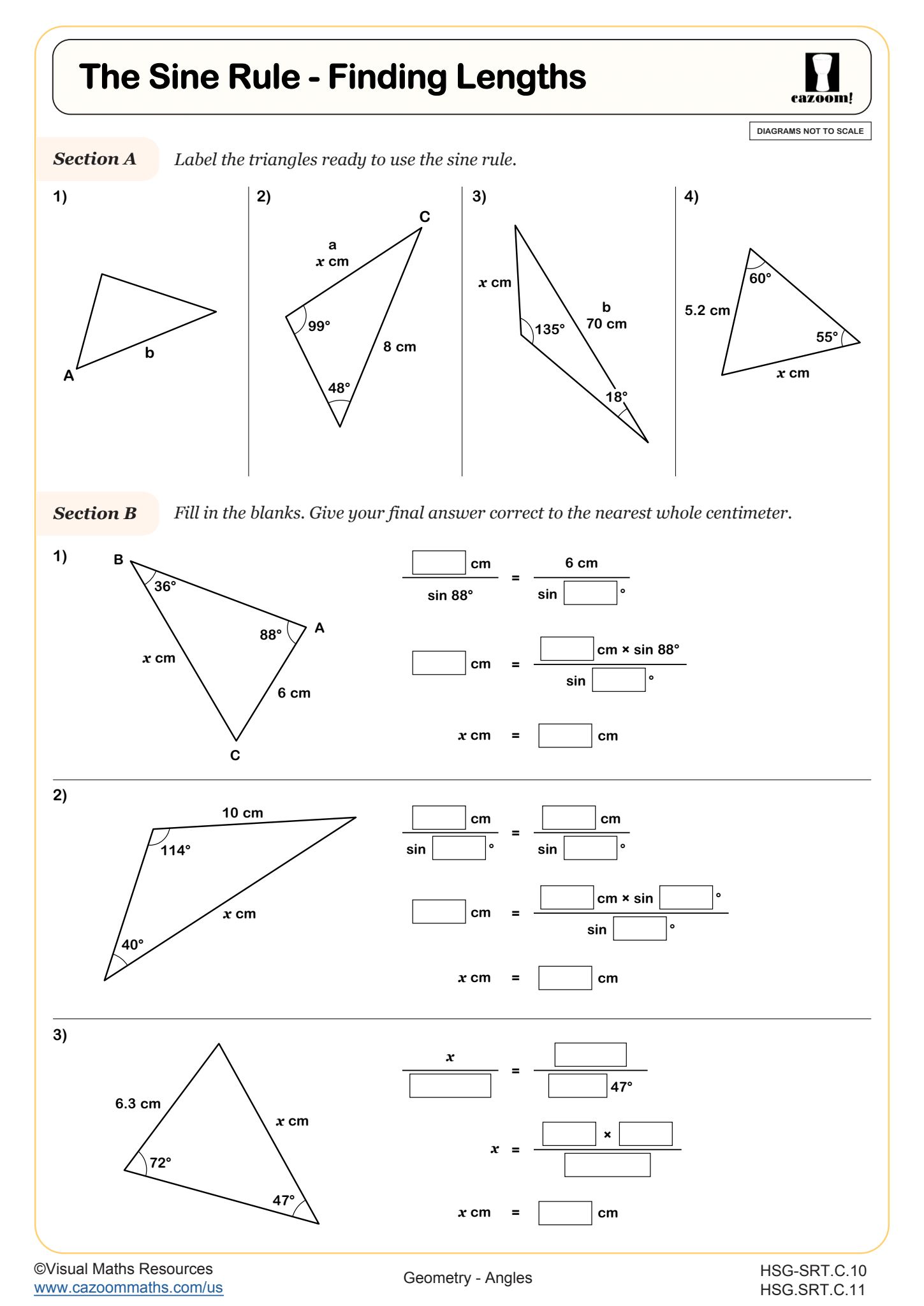
The Sine Rule - Finding Lengths
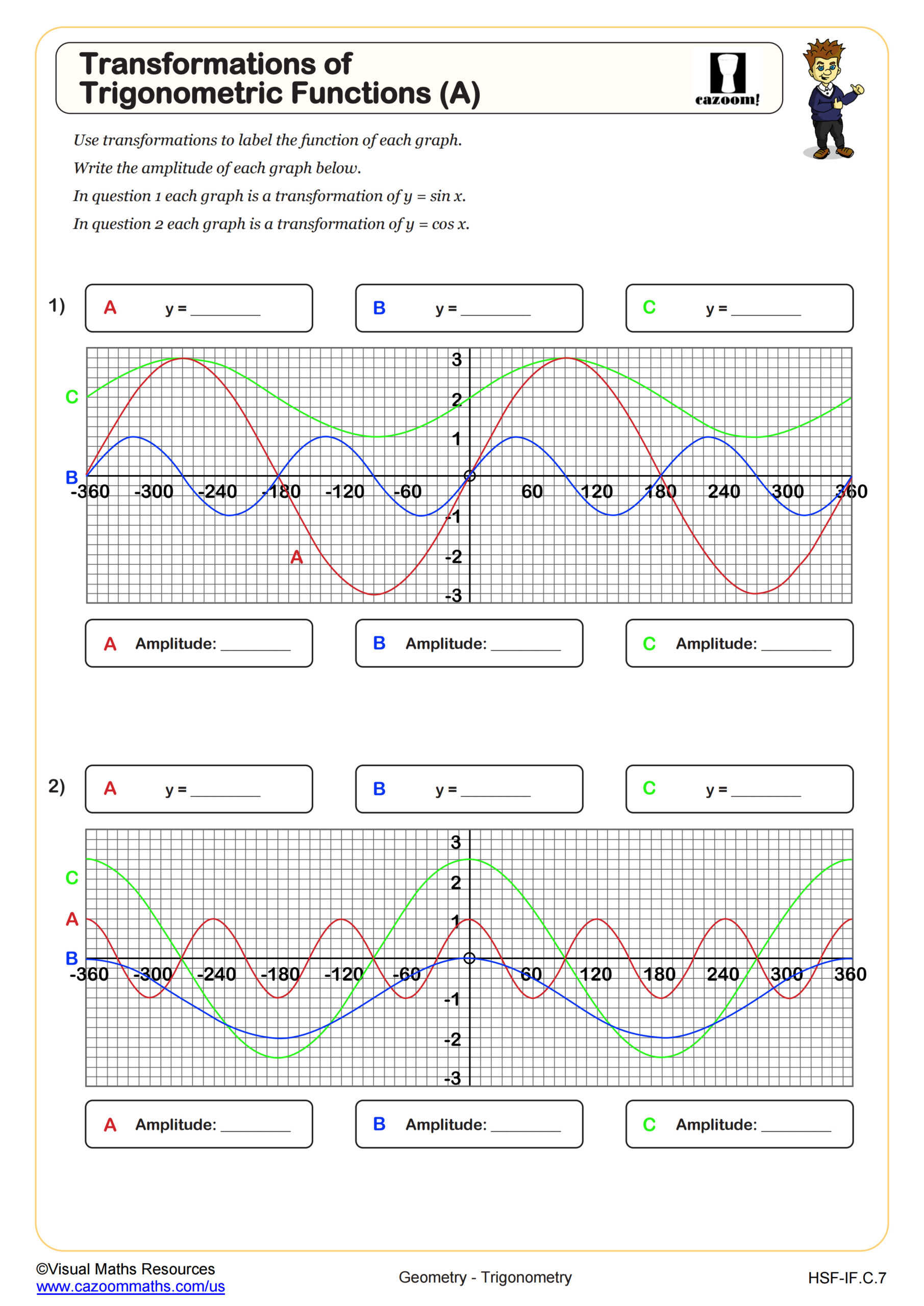
Transformations of Trigonometric Functions (A)
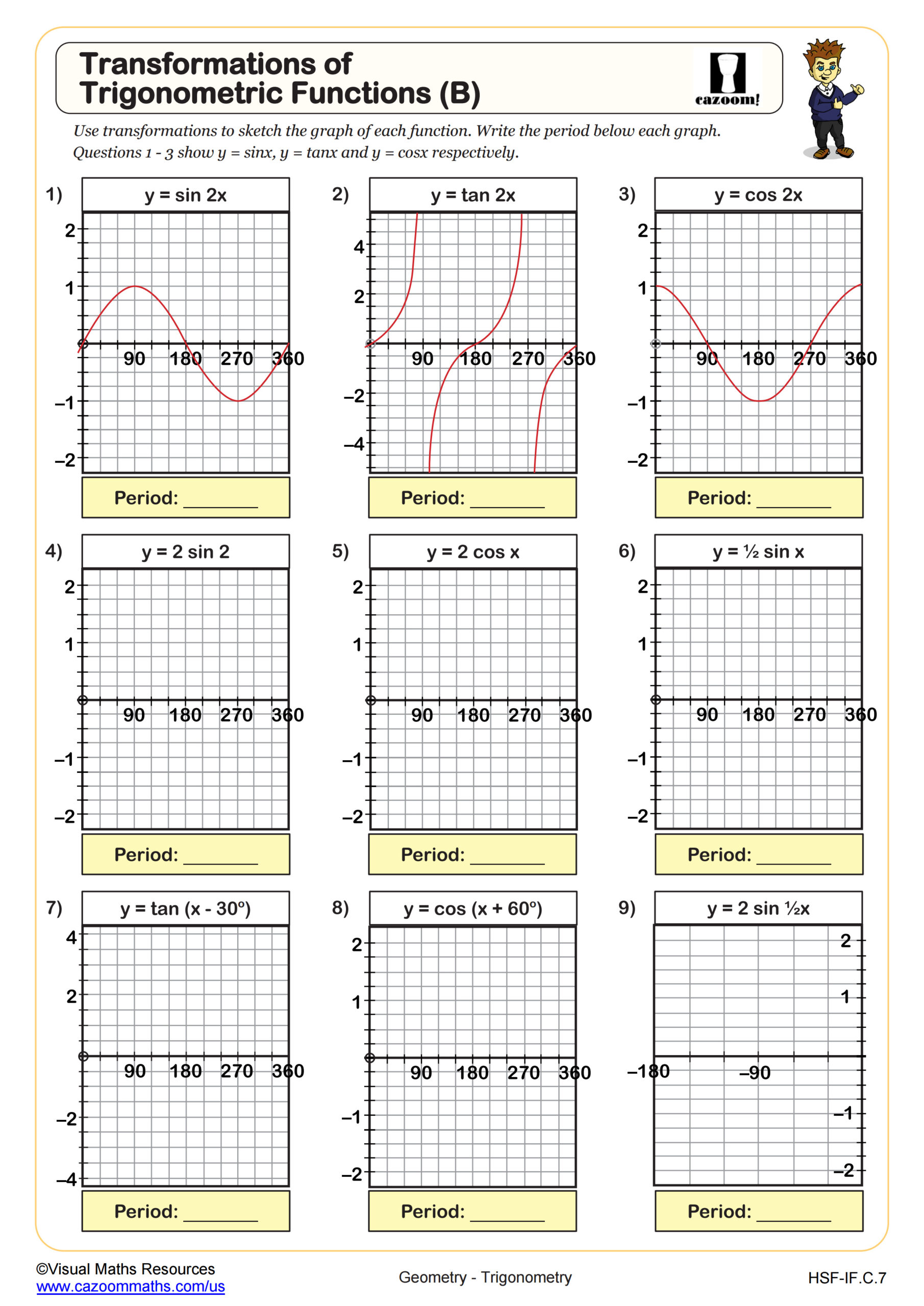
Transformations of Trigonometric Functions (B)
What Trigonometry Topics Are Covered in Integrated Math 3?
Integrated Math 3 trigonometry extends beyond right triangle ratios to include the Sine Rule and Cosine Rule for solving any triangle, graphing sine, cosine, and tangent functions, and analyzing transformations that affect amplitude, period, phase shift, and vertical translation. Students also explore inverse trigonometric functions and apply trigonometry to real-world problems involving navigation, surveying, and engineering contexts. This aligns with Common Core standards for advanced trigonometric applications and prepares students for precalculus.
Teachers frequently observe that students confuse when to apply the Sine Rule versus the Cosine Rule. The key distinction becomes clearer when students learn that the Sine Rule works best with angle-side opposite pairs, while the Cosine Rule handles cases where two sides and the included angle are known, or when all three sides are given and an angle must be found.
How Does Trigonometry Appear on the SAT and ACT?
Both the SAT and ACT test trigonometric concepts, though the SAT includes fewer trig questions overall. Students need to interpret trigonometric graphs, identify amplitude and period from equations, solve for angles using inverse functions, and apply the unit circle. The ACT includes more extensive trigonometry coverage, testing the Sine Rule, Cosine Rule, and transformations of trigonometric functions. Questions often embed trigonometry within coordinate geometry or require students to model periodic phenomena.
Students lose points when they forget to set their calculators to degree mode versus radian mode, particularly on multiple-choice questions where both radian and degree answer choices appear. Another common assessment error occurs when students misidentify the period of transformed functions, forgetting that the coefficient affects period differently for sine and cosine than it does for tangent functions.
What Is the Cosine Rule and When Should Students Use It?
The Cosine Rule (also called the Law of Cosines) provides a formula for finding unknown sides or angles in any triangle, not just right triangles: a² = b² + c² - 2bc cos(A). Students apply this rule when they know two sides and the included angle, or when they know all three sides and need to find an angle. The formula extends the Pythagorean theorem to non-right triangles and becomes the foundation for solving oblique triangle problems throughout STEM fields.
Engineers and surveyors regularly use the Cosine Rule to calculate distances that cannot be measured directly. For example, determining the distance across a lake, finding the span of a bridge support, or calculating property boundaries all require this technique. GPS technology relies heavily on these triangulation principles to pinpoint locations, making the Cosine Rule a practical tool in modern navigation systems and mapping applications.
How Can Teachers Use These Trigonometry Worksheets in Integrated Math 3?
These worksheets provide structured practice that builds from basic application of the Sine and Cosine Rules through complex graph transformations. The progressive difficulty allows teachers to differentiate instruction, assigning foundational worksheets for students still developing confidence while challenging advanced students with transformation problems involving multiple parameters. Complete answer keys enable students to check their work independently, making these worksheets suitable for homework, flipped classroom models, or self-paced review.
Many teachers use these worksheets during test preparation, particularly before unit assessments or state exams. The graph transformation worksheets work well for paired activities where one student describes changes in amplitude or period while the partner sketches the resulting function. Teachers also find these resources valuable for intervention sessions, allowing students who missed class or need additional support to work through problems systematically with immediate feedback from the answer keys.