Kindergarten Properties of Operations Worksheets
Making 10

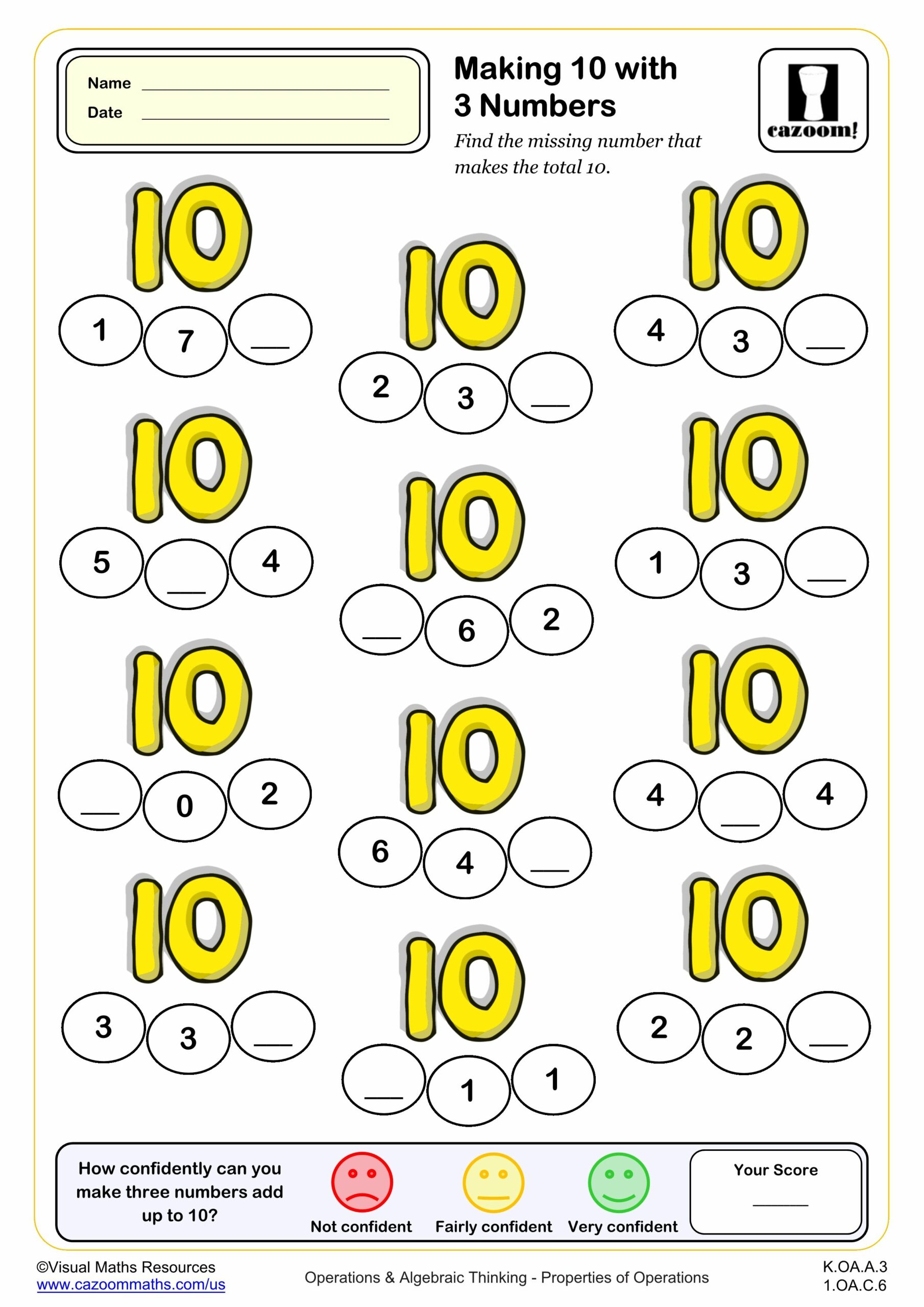
Making 10 with three numbers
Making 15

Making 15 (BONDS)

Making 18

Making 18 (BONDS)

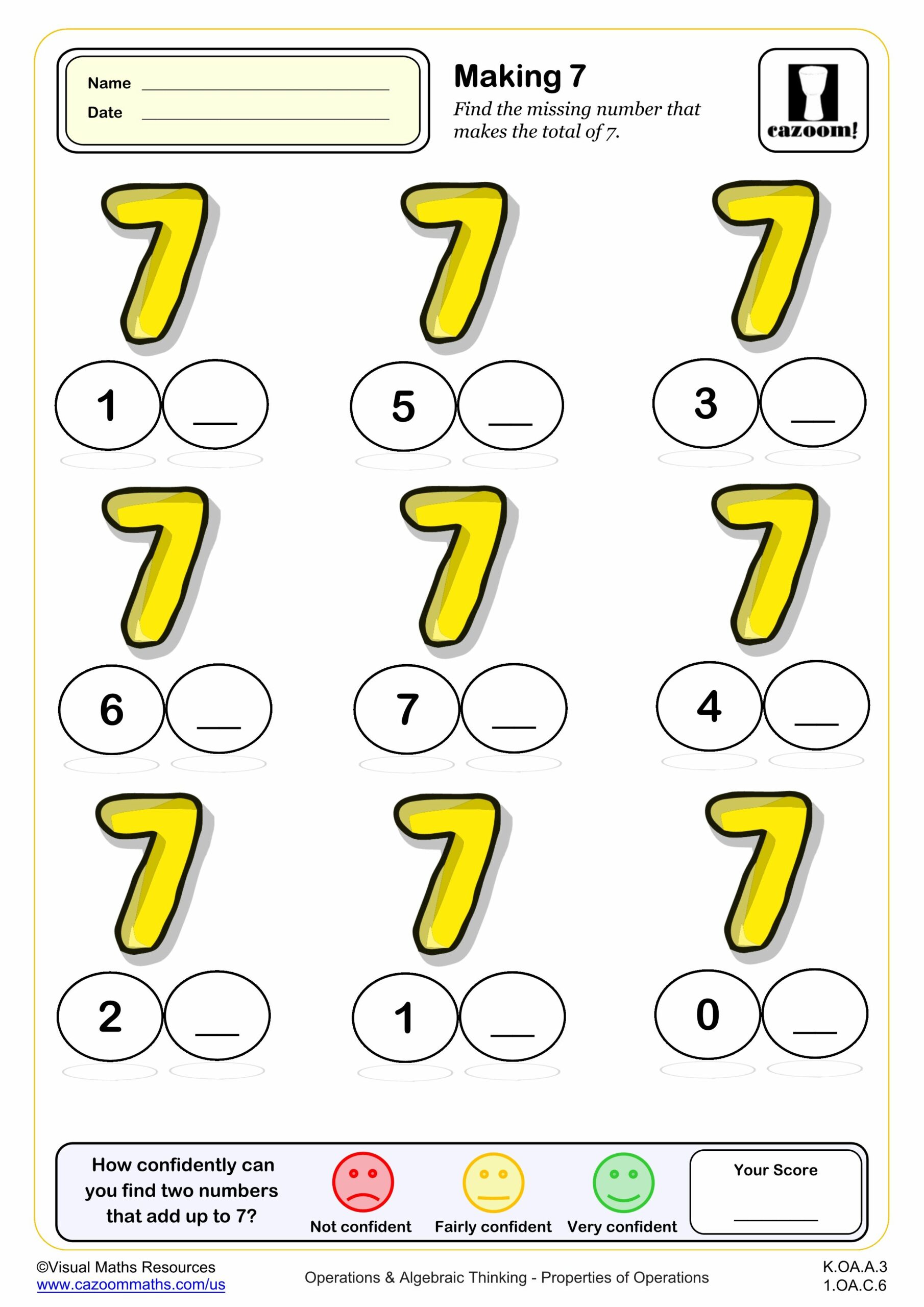
Making 7
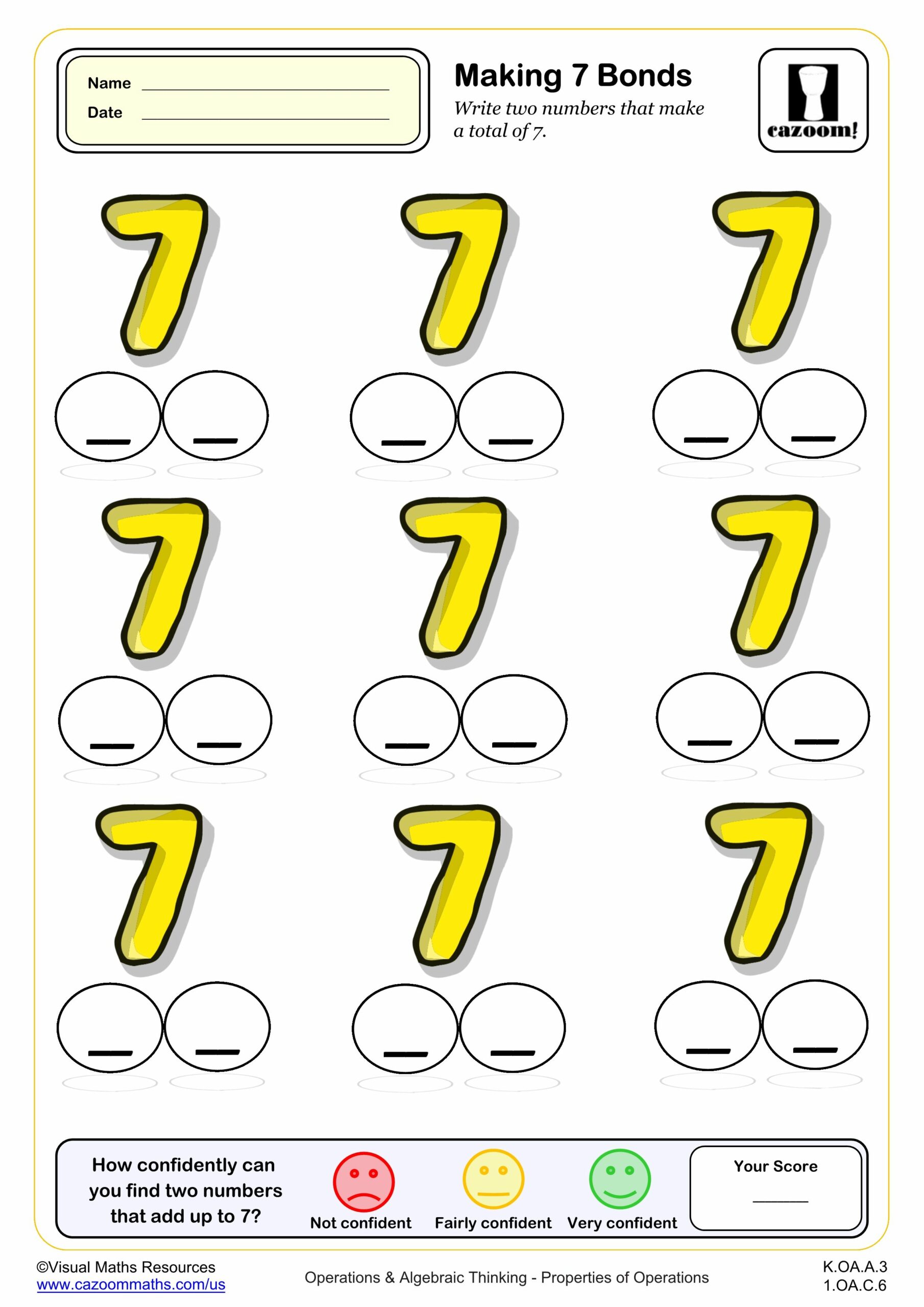
Making 7 (Bonds)
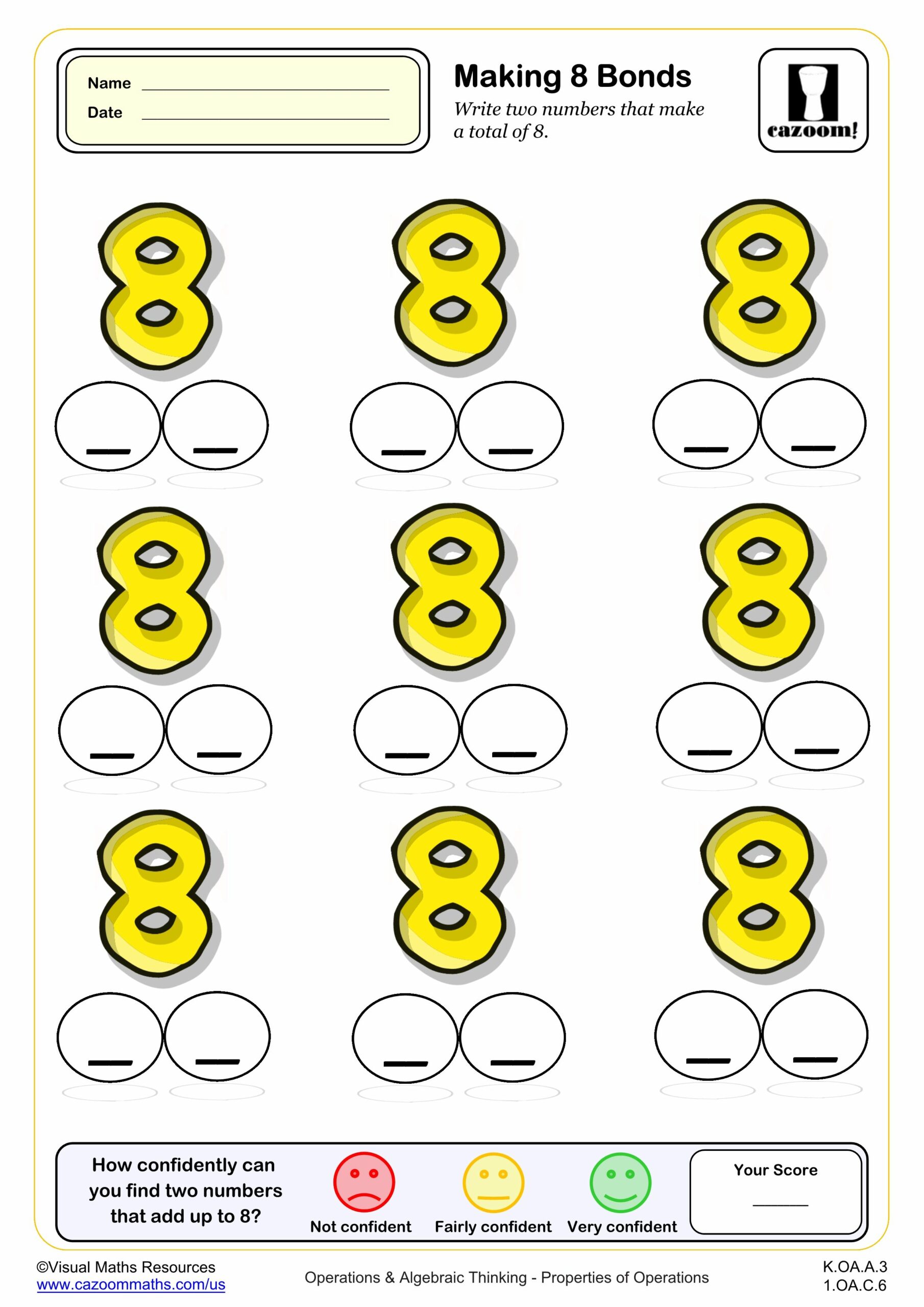
Making 8 (BONDS)
Making 9 (BONDS)

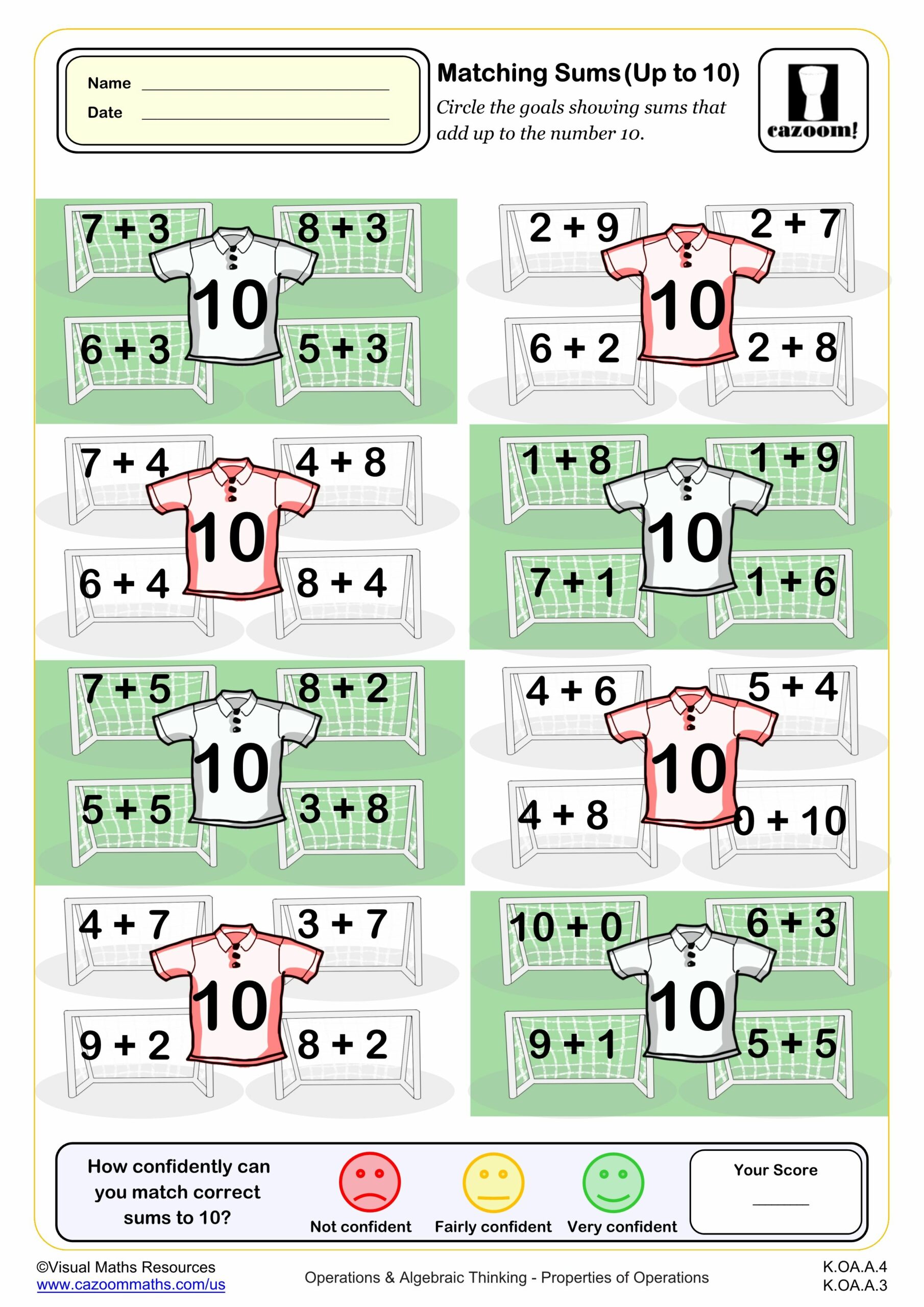
Matching Sums (to 10)
Number Bonds to 10 drills (10 questions)

Number Bonds to 10 drills (20 questions)

Number Bonds to 10 drills (50 questions)

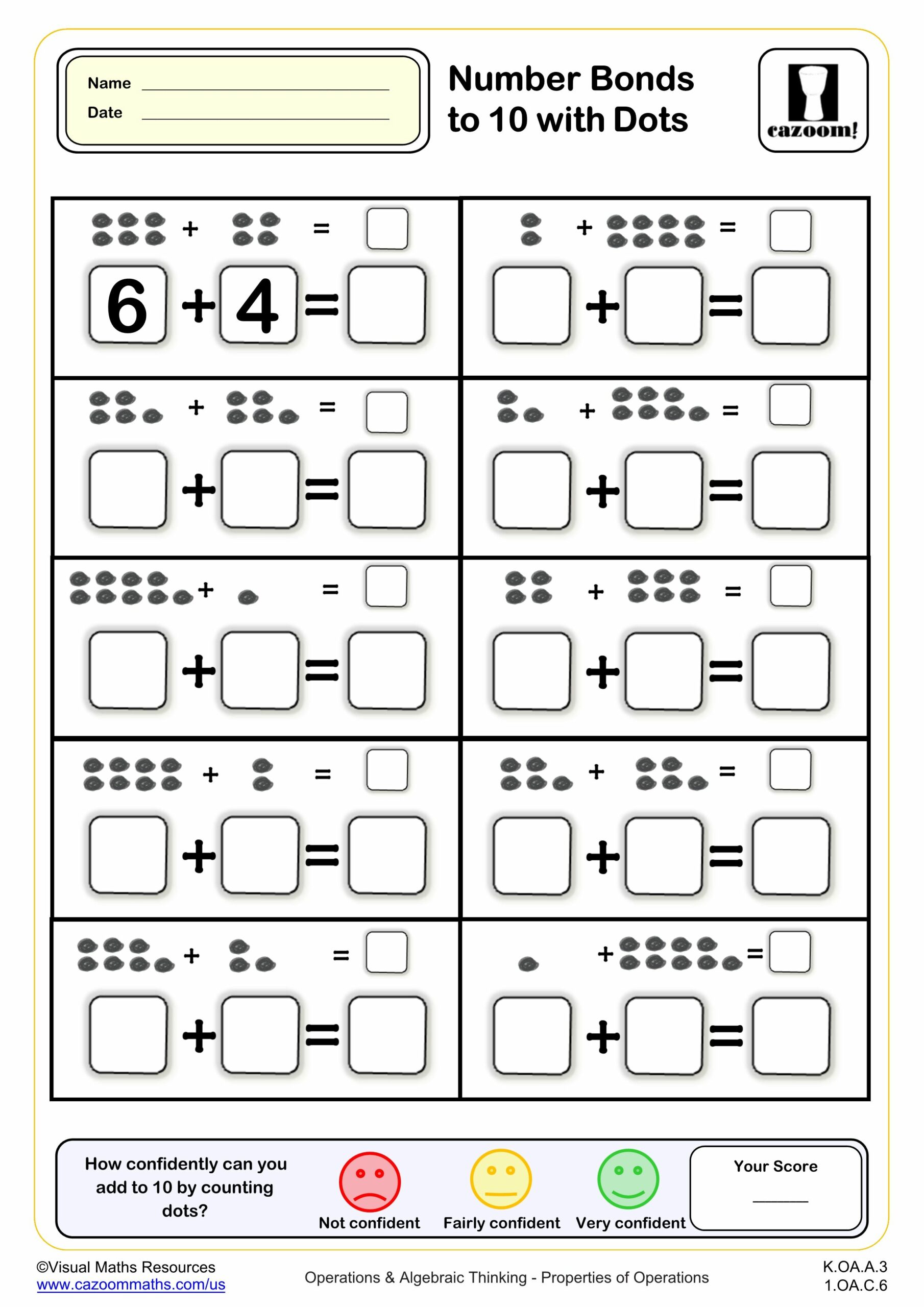
Number Bonds to 10 with Dots
Number bonds to 10 with number lines

Number Bonds to 5 drills (10 questions)

Number Bonds to 5 drills (20 questions)

Number Bonds to 5 drills (50 questions)

Subtracting 1 (10 questions)

Subtracting 1 (20 questions)

Subtracting 1 (50 questions)

Subtracting 2 (10 questions)

Subtracting 2 (20 questions)

Subtracting 2 (50 questions)

Subtracting Numbers Less Than 10 (A)

Subtracting Numbers Less Than 10 (B)

Subtracting Numbers Less Than 10 (C)

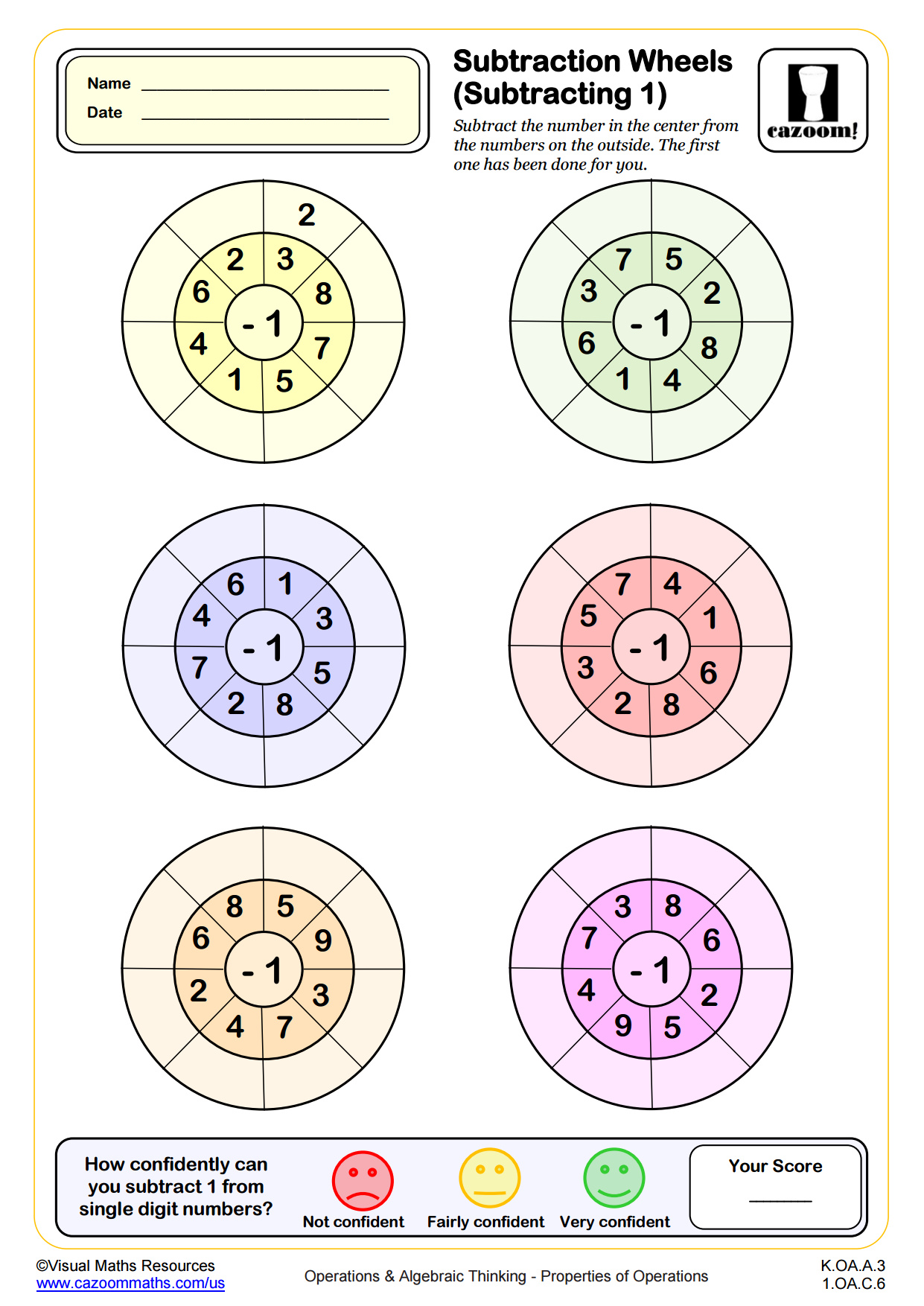
Subtraction Wheels (Subtracting 1)
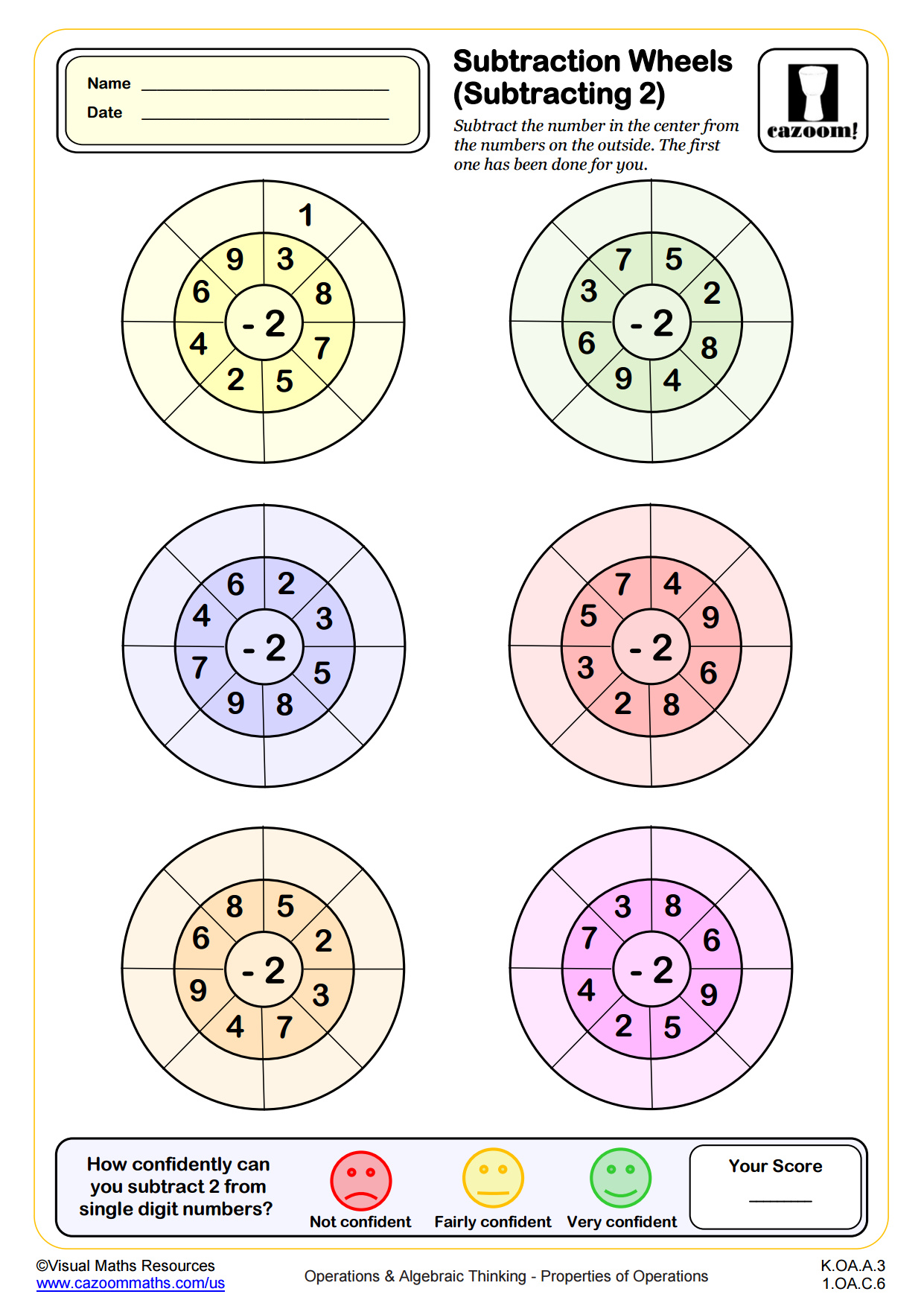
Subtraction Wheels (Subtracting 2)
Subtraction Wheels (Subtracting 5)
Subtraction Wheels (Subtracting up to 10) A
Subtraction Wheels (Subtracting up to 4)
What Are Properties of Operations in Kindergarten Math?
Properties of operations in kindergarten focus on the commutative property of addition (understanding that 3 + 2 equals 2 + 3) and the inverse relationship between addition and subtraction. At this level, students don't memorize formal property names but instead develop intuitive understanding through repeated practice with number bonds, fact families, and visual models. The Common Core State Standards for kindergarten emphasize fluently adding and subtracting within 5, which builds the foundation for recognizing these operational patterns.
A common misconception occurs when students believe subtraction works the same way as addition regarding order. Many young learners initially think 5 - 2 should equal 2 - 5 because they've learned that 5 + 2 equals 2 + 5. Teachers address this by using concrete manipulatives and contextual stories that highlight how subtraction represents taking away or finding the difference, where sequence matters. Number bond practice helps students visualize these relationships without confusion.
What Should Kindergarten Students Know About Properties of Operations?
Kindergarten students should recognize that any number can be decomposed and recomposed in multiple ways. For example, they should understand that 8 can be made from 5 + 3, 4 + 4, or 7 + 1, and that each combination still equals 8. Students at this stage should fluently add and subtract within 5 and work toward fluency within 10 by the end of the year. They should also understand that addition puts together and increases quantities while subtraction takes apart and decreases them.
This foundational work prepares students for first grade expectations, where they'll formally work with the commutative and associative properties and extend fluency to addition and subtraction within 20. Students who enter first grade without solid number sense and operational understanding often struggle with mental math strategies and fact mastery. The practice kindergarteners get with number bonds and basic fact drills creates the automatic recall that supports more complex problem-solving in subsequent grades.
How Do Number Bonds Help Students Understand Operations?
Number bonds are visual representations that show how a whole number can be split into parts. A number bond diagram typically shows one number at the top (the whole) connected to two numbers below (the parts), illustrating that 10 could be 6 and 4, or 7 and 3, or any other combination. This model helps students see the relationship between addition and subtraction concretely: if 6 + 4 = 10, then 10 - 6 must equal 4. Number bonds develop flexible thinking about numbers rather than rote memorization.
This conceptual understanding connects directly to real-world situations students encounter daily. When a child has 10 crayons and gives 3 to a friend, understanding number bonds helps them quickly determine they have 7 left. In early STEM learning, this part-whole thinking supports data analysis (comparing quantities in simple graphs) and measurement concepts (recognizing that 10 inches can be composed of different smaller lengths). Building this flexibility with small numbers creates mathematical thinkers rather than just calculators.
How Can Teachers Use These Worksheets Most Effectively?
These worksheets provide systematic practice that moves from smaller number ranges (bonds to 5) to larger ones (bonds to 10), allowing teachers to differentiate based on student readiness. The drill format builds automaticity, which is crucial at the kindergarten level where students are still developing one-to-one correspondence and number recognition. Teachers can use the answer keys for immediate feedback during independent work time or for quick checks during small group instruction, identifying which number combinations require additional practice.
Many teachers use these worksheets as warm-up activities at the start of math lessons or as quick assessments to monitor progress toward fluency benchmarks. The shorter worksheets with 10 questions work well for students who need success experiences with completing tasks, while the longer 50-question sets challenge advanced learners and provide comprehensive practice before assessments. Pairing students for worksheet completion encourages mathematical discussion, where one student solves while the other checks using manipulatives or mental strategies, building both computational skills and mathematical communication.