Back to:
Combining Translations and Reflections of Graphs WORKSHEET
Suitable for Grades: Algebra II, IM 1
CCSS: HSA.REI.D.11, HSA.REI.D.12
CCSS Description: Explain why the x-coordinates of the points where the graphs of the equations y = f(x) and y = g(x) intersect are the solutions of the equation f(x) = g(x); find the solutions approximately, e.g., using technology to graph the functions, make tables of values, or find successive approximations. Include cases where f(x) and/or g(x) are linear, polynomial, rational, absolute value, exponential, and logarithmic functions.★
Graph the solutions to a linear inequality in two variables as a half-plane (excluding the boundary in the case of a strict inequality), and graph the solution set to a system of linear inequalities in two variables as the intersection of the corresponding half-planes.
Graph the solutions to a linear inequality in two variables as a half-plane (excluding the boundary in the case of a strict inequality), and graph the solution set to a system of linear inequalities in two variables as the intersection of the corresponding half-planes.
Combining Translations and Reflections of Graphs WORKSHEET DESCRIPTION
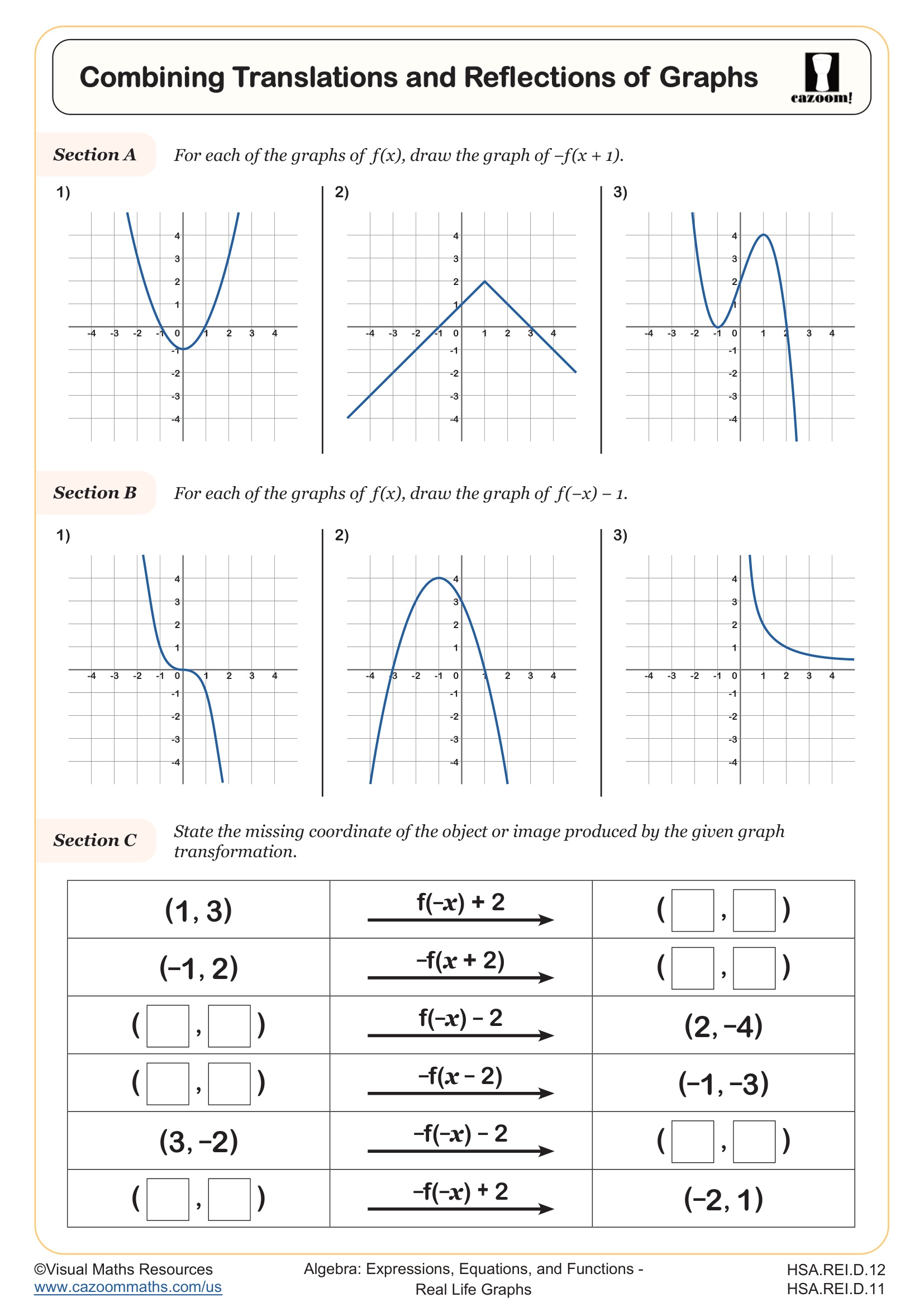
This worksheet follows on from Translating Graphs and Reflecting Graphs to combine two types of transformations. Section A asks learners to sketch a graph after a translation and then a reflection. Section B then asks for sketches of a reflection followed by a translation. Section C then focuses on coordinates before and after a combined transformation. Section D asks learners to match graphs to transformations given in function form and the worksheet ends with problems involving trigonometric graphs.
RELATED TO Combining Translations and Reflections of Graphs WORKSHEET
Frequently Asked Questions
This combining translations and reflections of graphs worksheet is designed for students in Algebra II and IM 1 and aligns with Common Core State Standards.


