4th Grade Division Worksheets
Dividing 2 Digit Numbers by 1 Digit Divisors (A)

Dividing 2 Digit Numbers by 1 Digit Divisors (B)

Dividing 2,3 and 4 Digit Numbers by 1 Digit Divisors (C)

Dividing 4 Digit Numbers by 1 Digit Divisors (D)

Dividing with One and Two Digit Divisors (A)

Dividing with One and Two Digit Divisors (B)

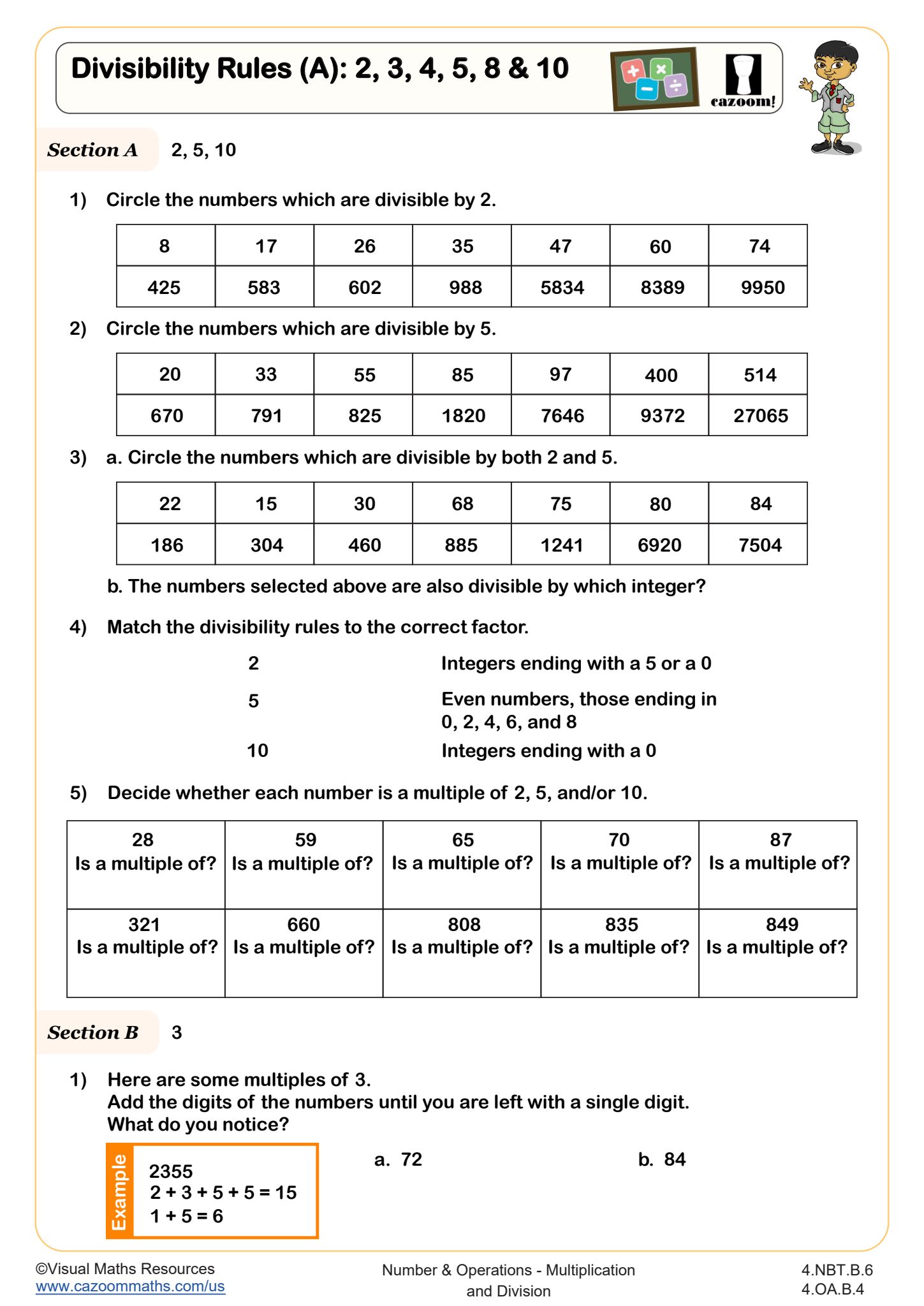
Divisibility Rules (A): 2, 3, 4, 5, 8 & 10
Division A (No Remainders)

What Are Divisibility Rules and Why Do 4th Graders Need Them?
Divisibility rules are shortcuts that help students determine whether a number can be divided evenly by another number without performing the actual division. Fourth graders typically learn rules for 2, 3, 4, 5, 8, and 10, which align with Common Core Standard 4.OA.B.4 and prepare students for factoring and fraction simplification in later grades. These rules build number sense and mental math abilities that students will use throughout their mathematical education.
Many students initially memorize the rules without understanding why they work, which limits their ability to apply them flexibly. Teachers find that students retain divisibility rules better when they test multiple examples and discover patterns themselves—for instance, recognizing that even numbers are divisible by 2, or that numbers ending in 0 or 5 are divisible by 5. Students frequently lose points on assessments when they confuse the rule for 3 (sum of digits divisible by 3) with the rule for 9, making practice with mixed problems particularly valuable.
What Division Skills Should 4th Grade Students Master?
By the end of 4th grade, students should fluently divide multi-digit numbers by one-digit divisors and understand the standard division algorithm with remainders. The Common Core Standards expect students to divide up to four-digit dividends by one-digit divisors and begin exploring division with two-digit divisors. Students should also interpret remainders in context—understanding when to round up, round down, or express the remainder as a fraction depending on the real-world situation.
This work builds directly on 3rd grade division with numbers up to 100 and prepares students for 5th grade decimal division and fraction operations. Teachers notice that students who struggle with place value concepts in earlier grades often hit a wall with multi-digit division because they can't estimate quotients or understand why digits go in specific places. The progression from dividing two-digit numbers to three and four-digit numbers helps students develop the procedural fluency and conceptual understanding needed for middle school mathematics.
How Does the Standard Division Algorithm Work?
The standard division algorithm (long division) is a step-by-step process where students divide, multiply, subtract, and bring down digits in sequence. Students start by determining how many times the divisor fits into the first digits of the dividend, write that number in the quotient, multiply it by the divisor, subtract the result, and bring down the next digit to continue the process. This algorithm works for any size numbers and provides a systematic approach that students will use through high school.
Division appears constantly in real-world contexts and STEM fields. When engineers calculate how many solar panels fit on a roof, when bakers determine how many batches a recipe makes, or when scientists divide data sets into equal groups for analysis, they're using division. Students who understand the algorithm can solve problems like dividing 156 students into groups of 12 or calculating how many 8-ounce servings come from a 64-ounce container. These practical applications help students see division as a tool for problem-solving rather than just a classroom procedure.
How Can Teachers Use These Division Worksheets Effectively?
The worksheets provide scaffolded practice that progresses from simpler one-digit divisors to more complex two-digit divisors, allowing teachers to differentiate instruction based on student readiness. The answer keys make them practical for independent work, allowing students to check their understanding immediately and identify error patterns. Teachers can use the divisibility rules worksheet as a quick warm-up or assessment tool, while the multi-digit division problems work well for developing procedural fluency.
Many teachers assign these worksheets for homework to reinforce classroom instruction or use them during math centers for small-group practice. They're particularly effective for intervention work with students who need additional practice with the division algorithm or who make consistent errors with place value. The worksheets also work well for paired activities where students solve problems independently and then compare strategies and answers. Teachers often notice that students benefit from completing one worksheet, reviewing errors with the answer key, and then attempting a similar worksheet to apply what they learned.