4th Grade Multiplication Worksheets
Column Method for Multiplying a 2 Digit Number by a Single Digit

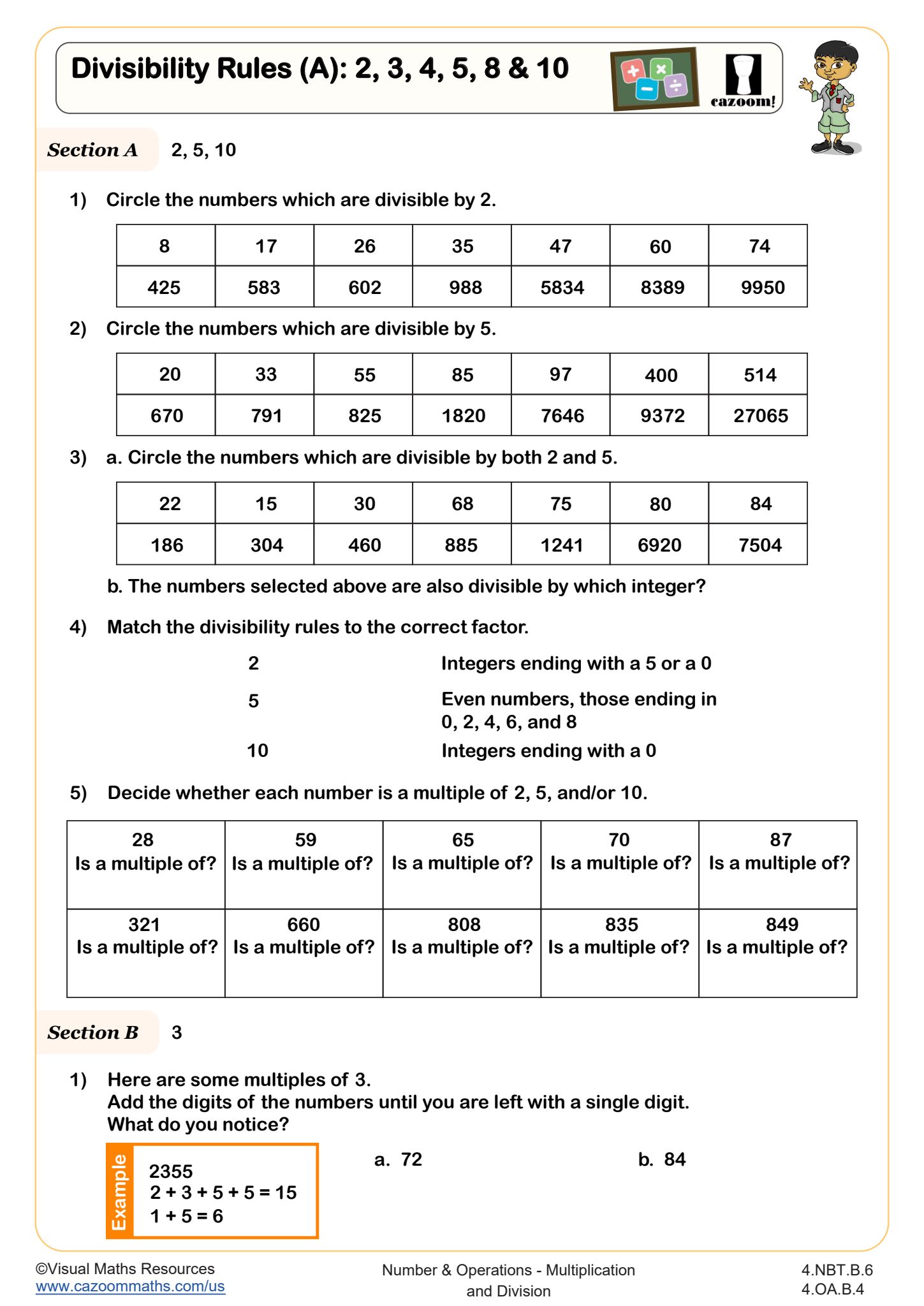
Divisibility Rules (A): 2, 3, 4, 5, 8 & 10
Divisibility Rules (B): 7, 9, 11
-7-9-11.jpg?w=3840)
Divisibility Rules (C): Combining Tests for Composite Factors
-Combining-Test-%20for-Composite-Factors.jpg?w=3840)
Factors

Identifying Prime Numbers

Investigating Prime Factors

LCM (Lowest Common Multiple)

Multiples

Multiply 2 Digits by 1 Digit

Multiplying 3 Digits by 1 Digit
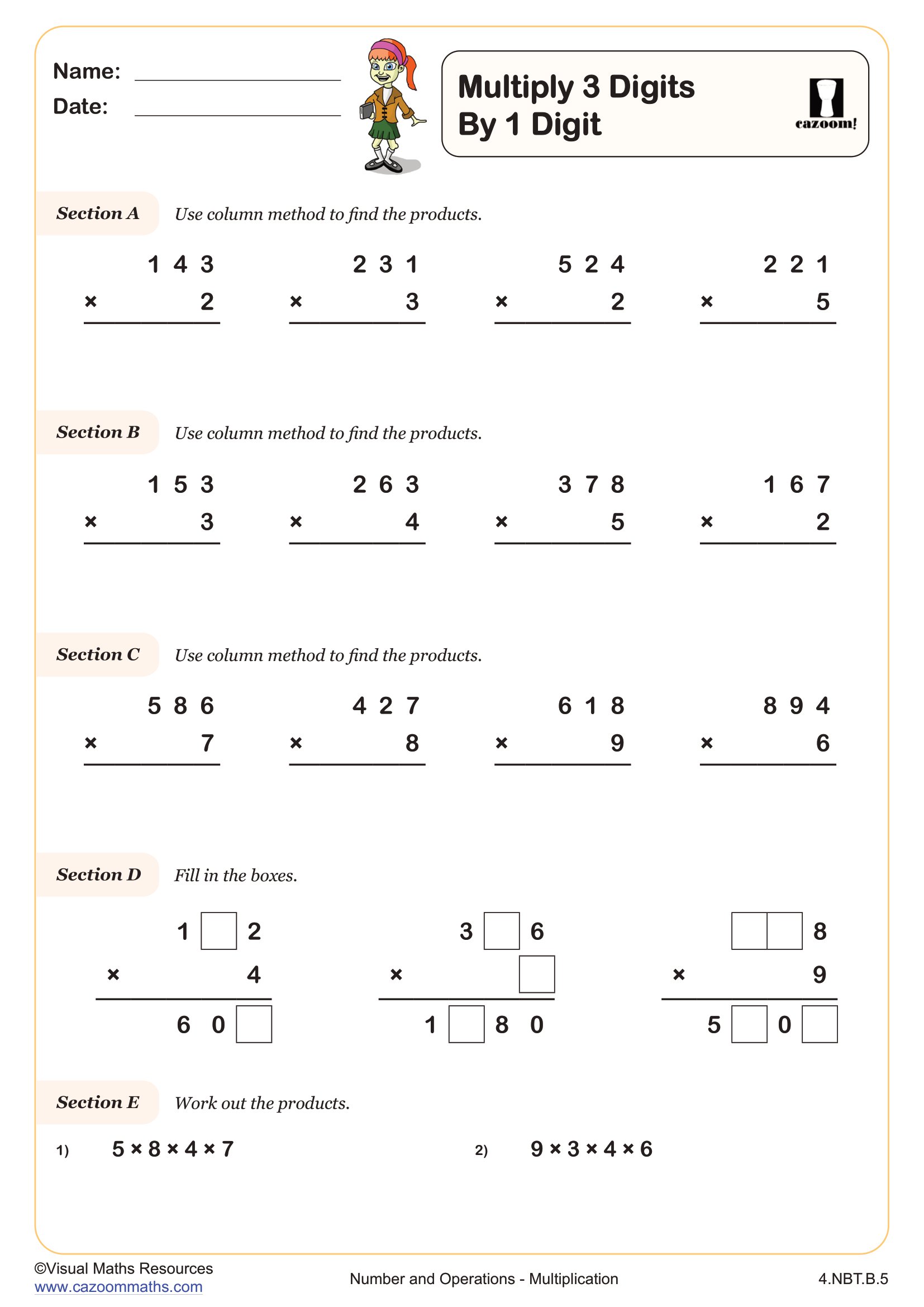
Multiplying by Multiples of Ten
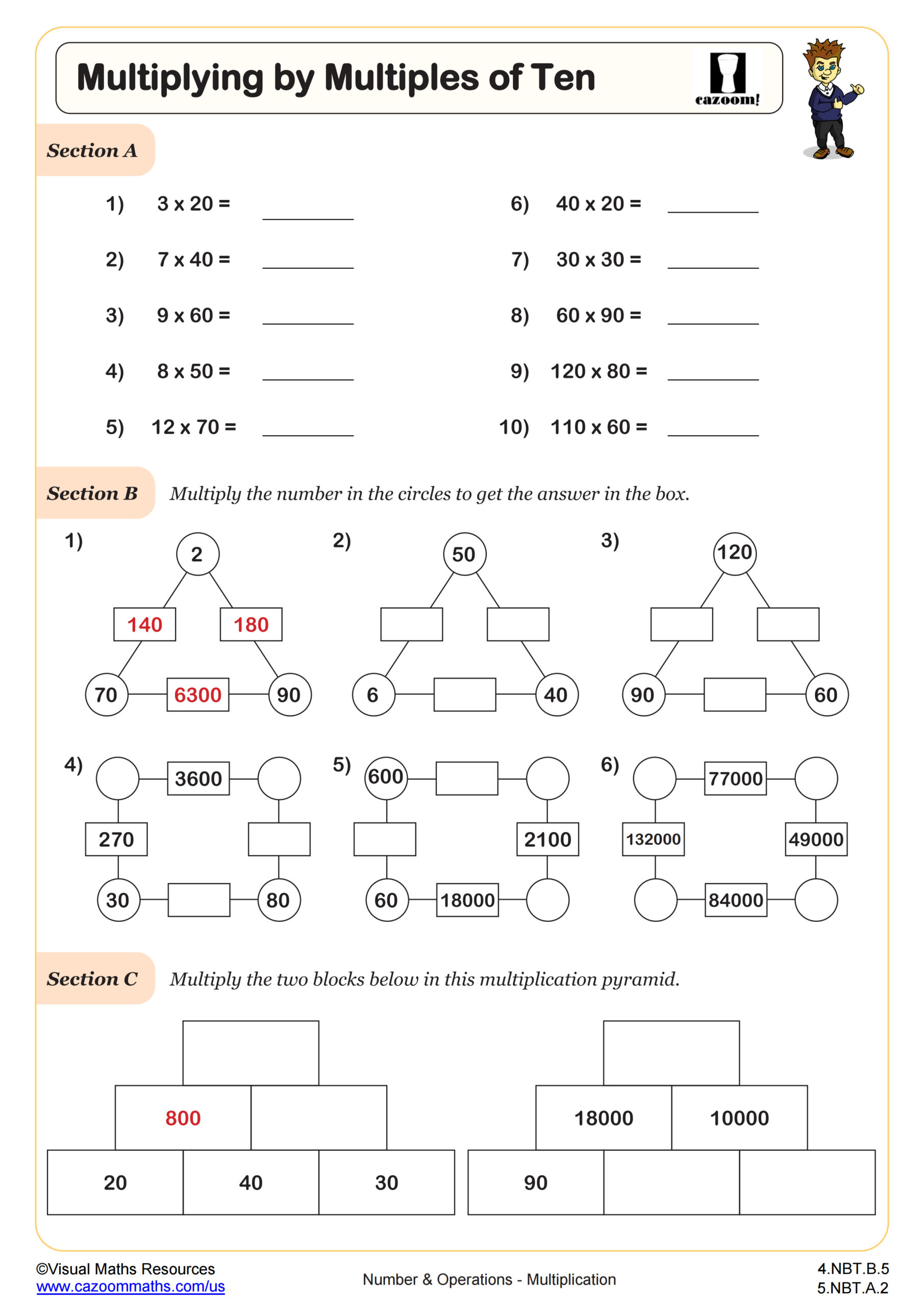
Multiplying by Two Digits Mentally
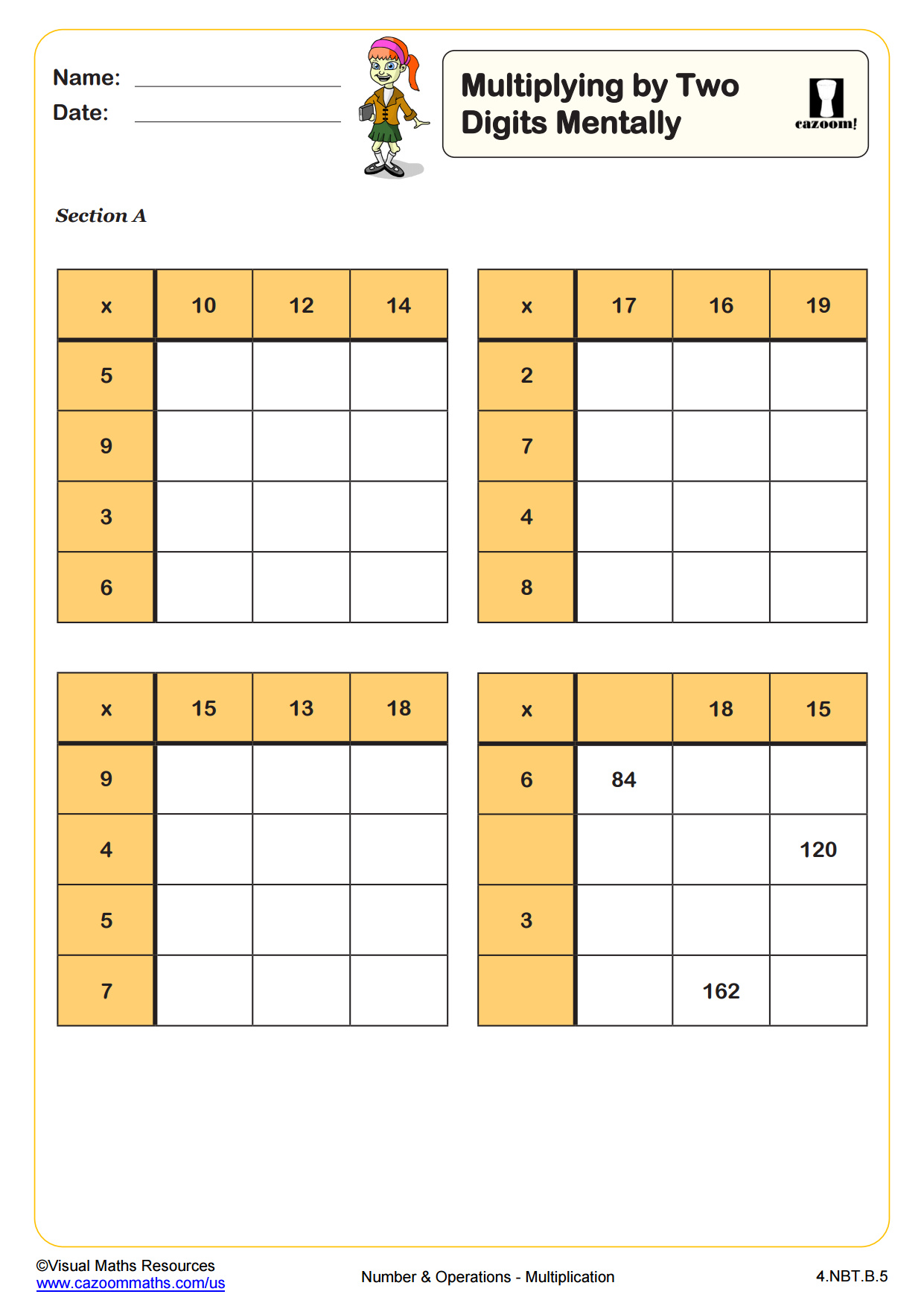
Practicing the box method for long multiplication

Practicing the Box Method for Multiplication (A)

Practicing the Column Method for Long Multiplication (A)

Practicing the Column Method for Long Multiplication (B)

Rangoli Color by Number - 2, 3 and 4 times tables
Rangoli Color by Number - 3, 6, 7, 8, 9 and 11 times tables
Using the Associative, Commutative and Distributive Properties for Multiplication

What multiplication skills should 4th graders focus on?
Fourth graders move beyond memorizing basic multiplication facts to applying strategies for multi-digit multiplication and understanding the mathematical relationships between factors and products. This includes mastering the column method and box method for problems like 43 × 27, recognizing divisibility patterns, and connecting multiplication to division as inverse operations. The Common Core State Standards expect students to multiply up to four-digit by one-digit numbers and two-digit by two-digit numbers using strategies based on place value and properties of operations.
Students often struggle with keeping place value aligned when using the column method, particularly when the second factor has a zero in the ones place. Teachers notice that students who understand why they "add a zero" when multiplying by the tens digit (because they're actually multiplying by 20, 30, or another multiple of ten) make fewer computational errors than those who follow the procedure without conceptual understanding.
How does 4th grade multiplication prepare students for middle school math?
In 4th grade, multiplication becomes the gateway to understanding factors, multiples, and prime factorization, all of which are prerequisite skills for fraction operations and algebraic thinking. Students should demonstrate fluency with multiplication facts through 12 × 12, apply the distributive property in multi-digit multiplication, and identify whether numbers are divisible by 2, 3, 4, 5, 8, 9, and 10 without performing complete division. This foundation directly supports 5th grade expectations for multiplying fractions and working with decimals.
The divisibility rules practiced in 4th grade become particularly valuable when students begin simplifying fractions in 5th and 6th grades. Students who recognize that 48 is divisible by 2, 3, 4, 6, 8, and other factors can quickly identify the greatest common factor needed to reduce fractions like 48/72. Many teachers find that time invested in building strong divisibility pattern recognition in 4th grade significantly reduces struggles with rational number operations in later grades.
What is the box method for multiplication and why do students use it?
The box method (also called area model or grid method) breaks multi-digit multiplication into smaller, more manageable partial products by partitioning numbers according to place value. For example, to solve 24 × 36, students create a 2×2 grid, breaking 24 into 20 + 4 and 36 into 30 + 6, then multiply each combination in separate boxes: 20×30, 20×6, 4×30, and 4×6, before adding the four partial products. This visual strategy helps students understand why the standard algorithm works and makes the distributive property explicit rather than abstract.
The box method connects directly to area calculations in geometry and construction planning. Architects and landscape designers use this same strategy when calculating materials needed for rectangular spaces with dimensions like 23 feet by 47 feet, mentally breaking the problem into (20+3) × (40+7) to estimate square footage. This approach also strengthens algebraic thinking, as the same box structure applies when students later multiply binomials like (x+3)(x+7) in middle school algebra.
How can teachers use these multiplication worksheets effectively in 4th grade classrooms?
These worksheets provide structured practice that builds from foundational skills to more complex applications, with each answer key allowing students to self-check work during independent practice or math centers. The progression from basic divisibility rules to combining tests for composite factors mirrors the scaffolding approach that helps students internalize patterns before applying them in multi-step problems. Teachers can use the engaging color-by-number activities to differentiate instruction, offering visual learners an alternative entry point to times table practice while maintaining grade-level rigor.
Many teachers incorporate these worksheets during warm-ups to maintain fact fluency, assign them as homework with answer keys sent home for family support, or use specific pages for intervention with students who need additional practice with particular multiplication strategies. The variety of formats works well for paired practice where one student solves while another checks using the answer key, promoting mathematical discussion about different solution methods. Standardized test preparation benefits from regular practice with long multiplication methods, as state assessments typically include multi-digit multiplication without calculators in 4th grade.