Algebra I Quadratic and Cubic Functions Worksheets
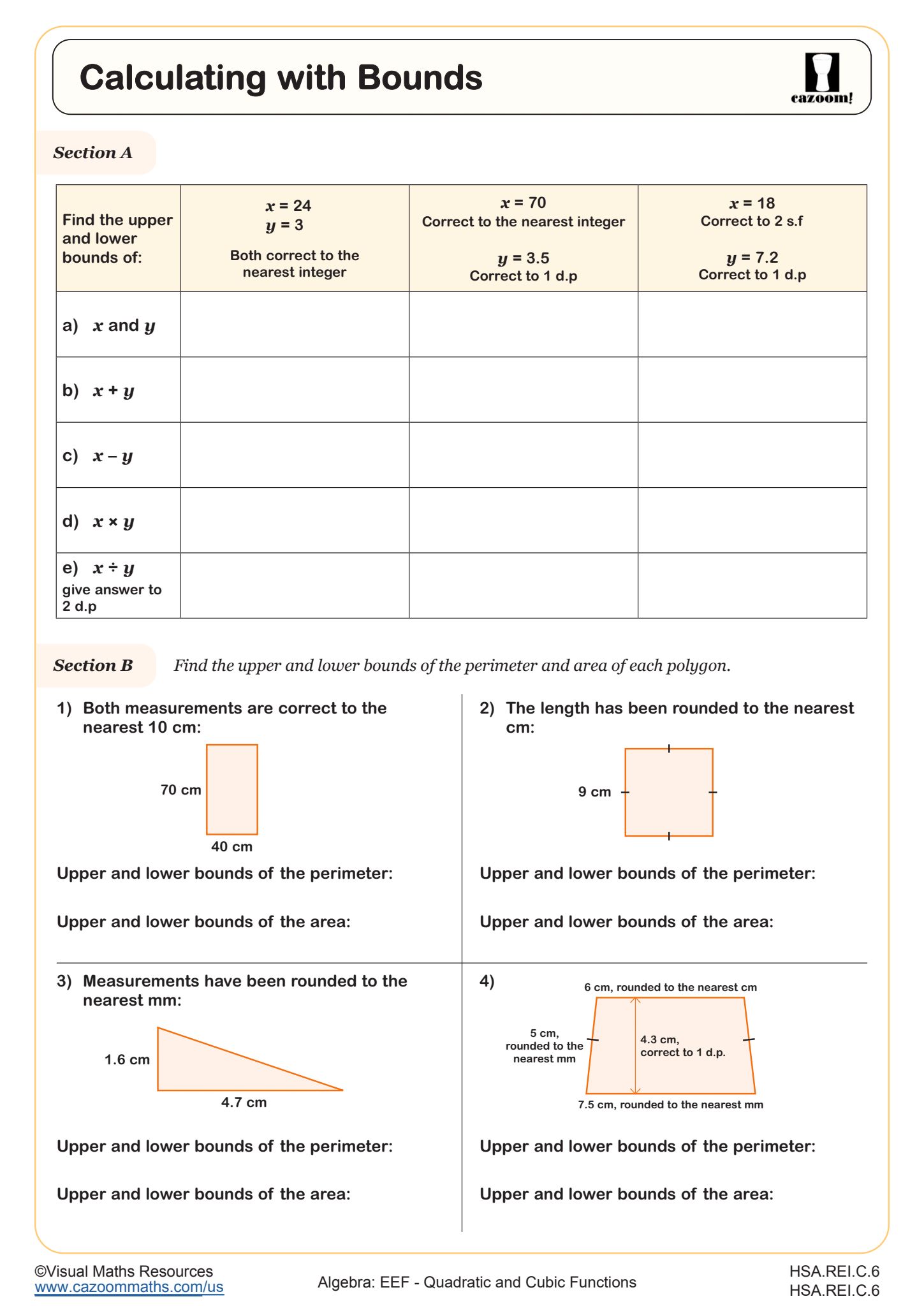
Calculating with Bounds
Completing the Square

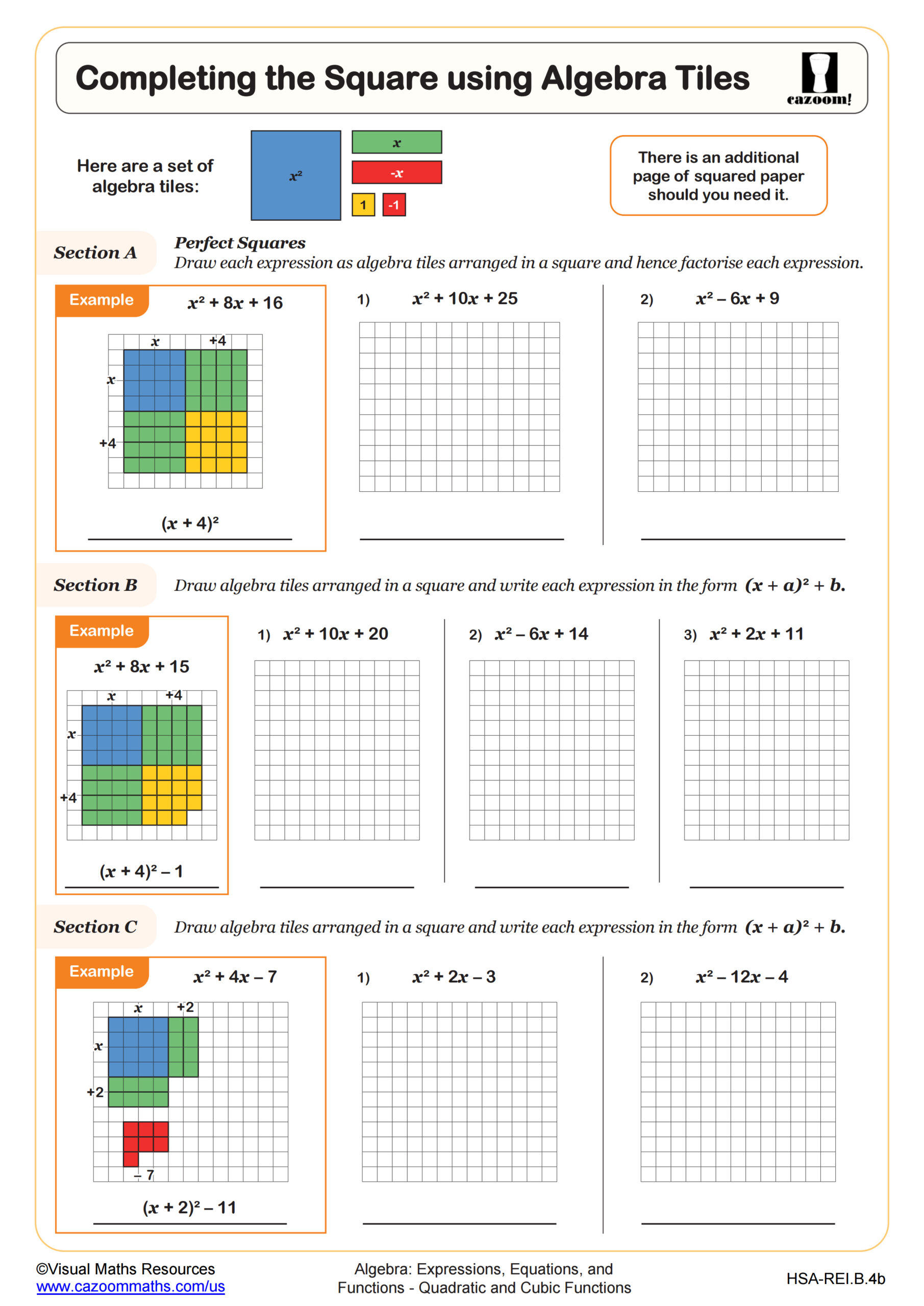
Completing the Square using Algebra Tiles
Factorising Quadratic Expressions - Using the Area Model

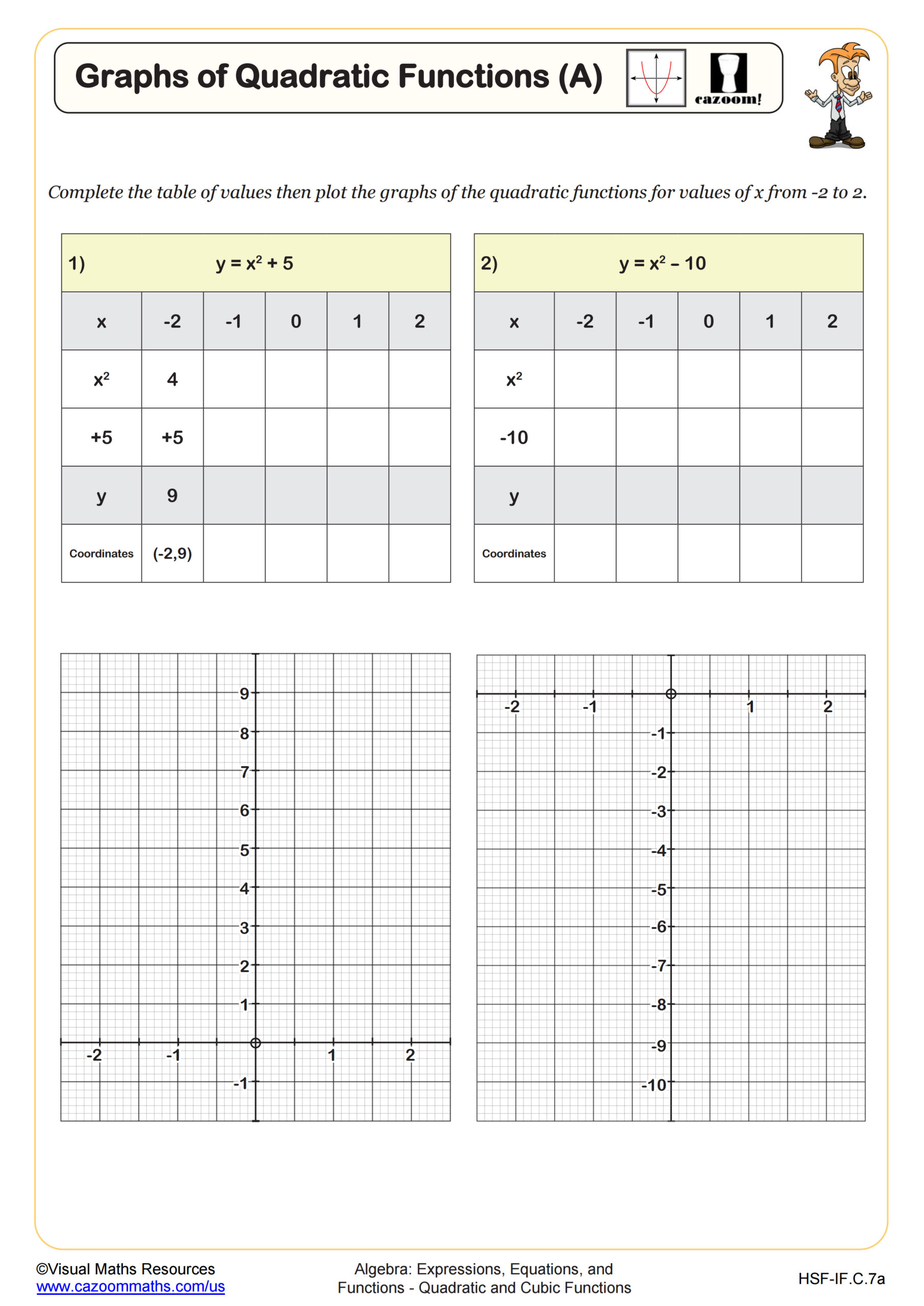
Graphs of Quadratic Functions (A)
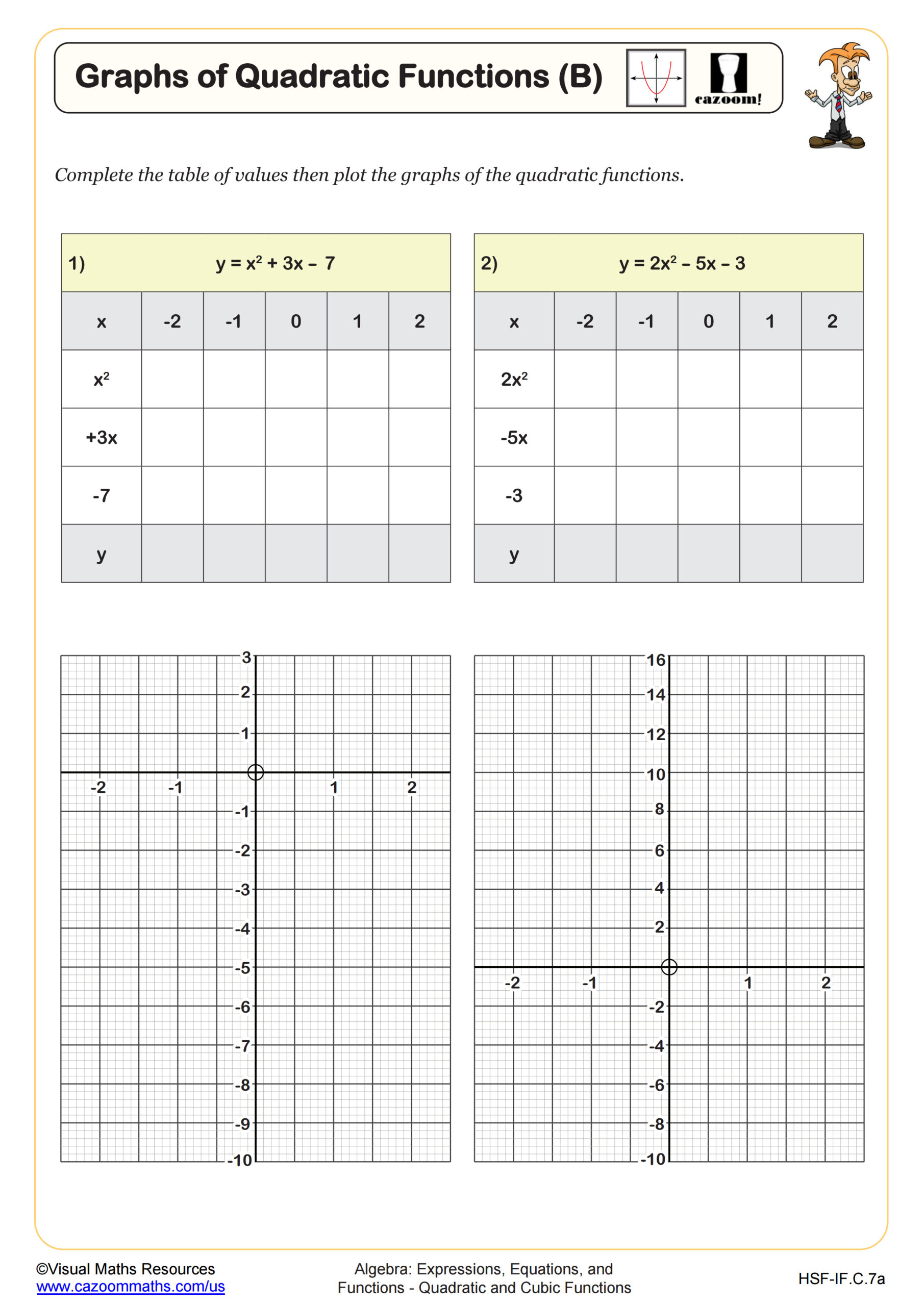
Graphs of Quadratic Functions (B)
Identifying Vertex of Quadratic Functions

Sketching Quadratic Functions
Solving Linear Simultaneous Equations - Same Coefficients

Substituting into Quadratic Expressions
What Skills Do Students Practice with Quadratic and Cubic Functions in Algebra I?
Students work with quadratic expressions and equations through multiple approaches aligned with Common Core standards for Algebra I. The worksheets cover substituting values into quadratic expressions, factoring using various methods, solving equations by factoring and completing the square, and understanding how quadratic functions behave graphically. While cubic functions appear less extensively in Algebra I than in later courses, students begin recognizing their characteristics and comparing them to quadratic behavior.
A common stumbling block occurs when students attempt to factor quadratic expressions without first checking for a greatest common factor. Teachers often see students jump straight to finding two numbers that multiply to give the constant term, missing opportunities to simplify the expression first. The area model worksheets address this by having students physically organize terms, which helps them visualize the factoring process and catch errors before they become ingrained habits.
How Do Quadratic Functions Appear on the SAT and State Assessments?
Standardized tests expect students to solve quadratic equations using the most efficient method for each situation, identify key features of parabolas from equations or graphs, and apply quadratic models to real-world contexts. The SAT Math section regularly includes problems requiring students to complete the square to find vertex form, factor to find zeros, or determine how changing a coefficient affects the graph. State assessments often test whether students can connect multiple representations of the same quadratic function and explain their reasoning.
Students lose significant points when they attempt to use the quadratic formula for every problem, even when factoring would be faster and less prone to arithmetic errors. Another common assessment mistake occurs when students correctly complete the square but forget to apply the correct sign when writing vertex form, particularly with expressions like x² + 6x where the constant term added and subtracted causes confusion. Regular practice identifying which solution method fits each problem type builds both accuracy and speed.
Why Is Completing the Square Important Beyond Just Solving Equations?
Completing the square transforms a quadratic function from standard form into vertex form, revealing the parabola's maximum or minimum point and axis of symmetry without graphing. This technique requires students to understand that adding and subtracting the same value keeps an equation balanced while creating a perfect square trinomial. The algebra tiles approach helps visual learners see why the process works: they're literally building a complete square from the x² and x terms, then accounting for the extra pieces needed to fill the shape.
Engineers and physicists use this technique when analyzing projectile motion, where finding the maximum height of an object requires identifying the vertex of the parabolic path. In computer graphics, programmers complete the square to optimize rendering algorithms for parabolic curves. College-bound students encounter this skill again in Precalculus when working with conic sections, where completing the square for both x and y variables reveals the center and radius of circles or the vertices of ellipses and hyperbolas.
How Can Teachers Use These Worksheets to Support Different Learning Needs?
The worksheets progress from concrete methods like area models and algebra tiles toward purely symbolic manipulation, allowing teachers to differentiate based on where students are in their understanding. Visual representations on early worksheets help struggling students build conceptual understanding before tackling abstract algebraic procedures, while more advanced students can move quickly to completing the square algebraically. The answer keys enable students to check their work immediately during independent practice, helping them catch and correct errors before patterns become habits.
Many teachers use these worksheets for targeted intervention when formative assessments reveal gaps in specific skills like factoring or for test preparation when students need focused practice before unit exams or state assessments. The range of problem types makes them suitable for paired work where students compare solution methods, small group instruction targeting particular misconceptions, or homework assignments that reinforce classroom learning. Having answer keys readily available means student teachers or paraprofessionals can effectively support small groups while the classroom teacher works with students needing more intensive help.