Algebra II Sequences Worksheets
What sequence concepts do Algebra II students need to master?
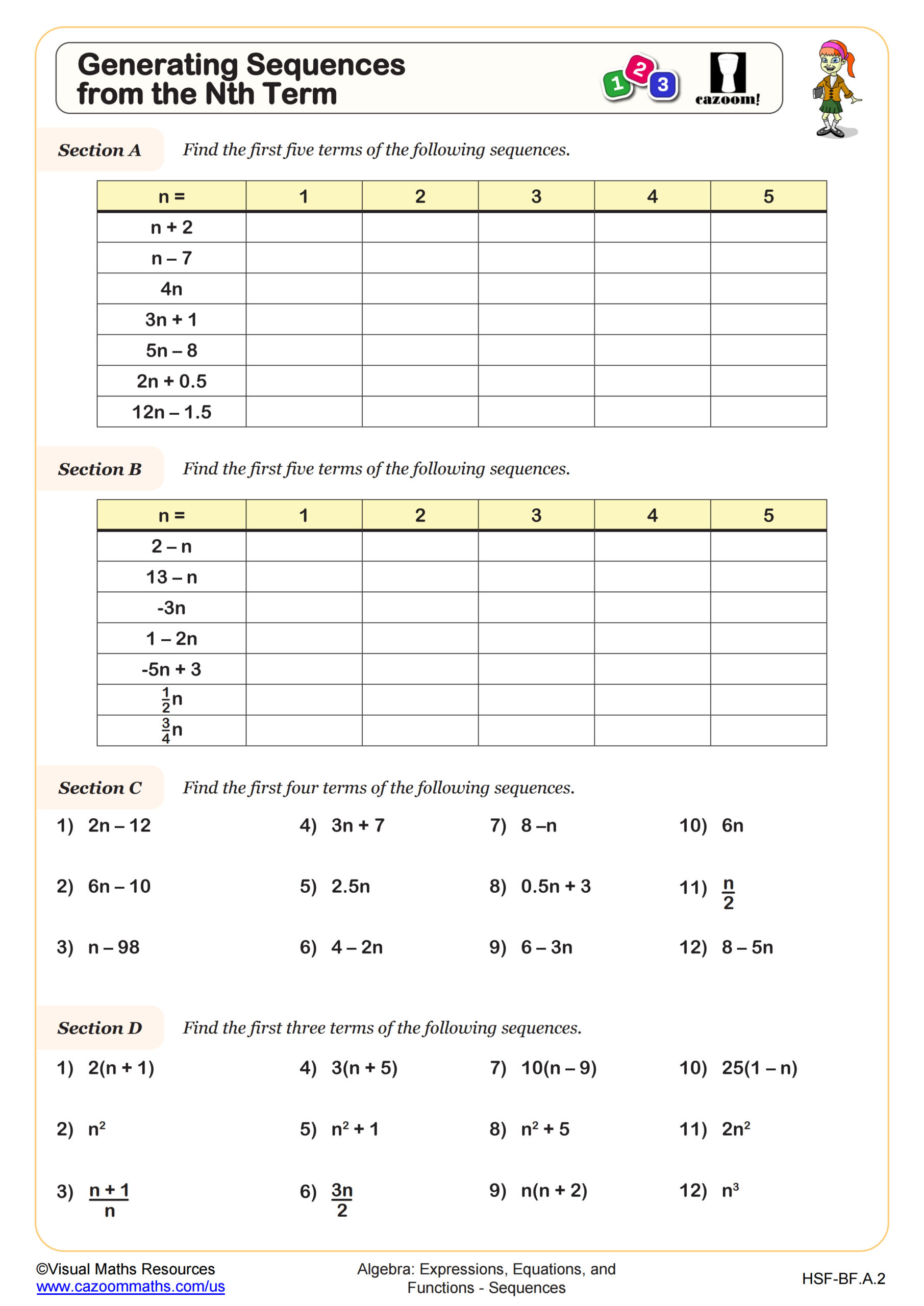
Algebra II sequence standards focus on both arithmetic and geometric sequences, requiring students to write explicit formulas, find nth terms, and distinguish between different sequence types. Students learn to identify common differences in arithmetic sequences and common ratios in geometric sequences, then apply these patterns to write general formulas. Teachers frequently notice that students confuse the formulas for arithmetic sequences (a_n = a_1 + (n-1)d) and geometric sequences (a_n = a_1 × r^(n-1)), particularly under test conditions.
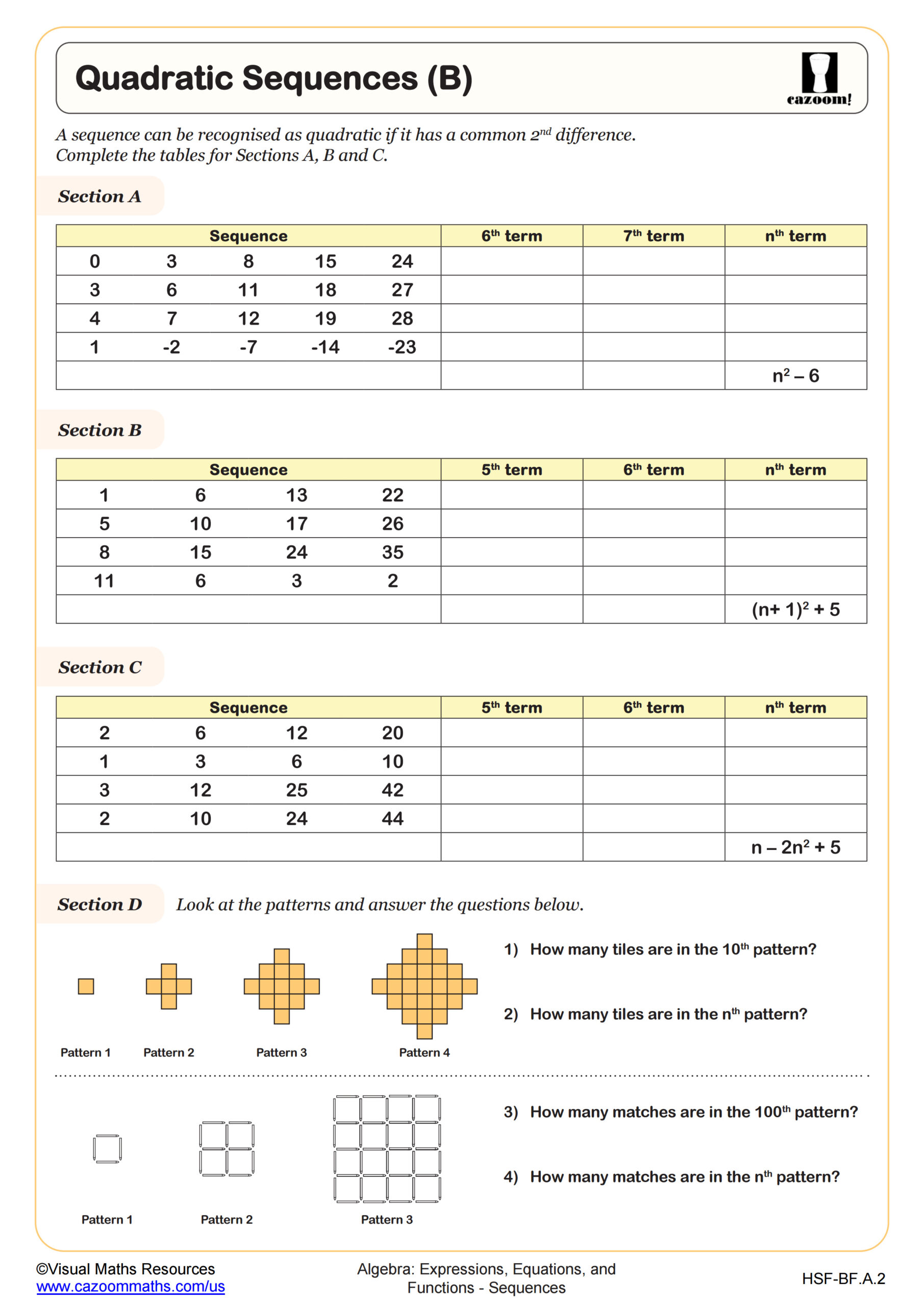
The curriculum also introduces special sequences, including Fibonacci sequences and triangular numbers, which appear in mathematical modeling and computer science applications. Students practice generating sequences from nth term formulas, a skill that reinforces function notation and prepares them for series in Pre-Calculus. Common Core State Standards expect students to interpret sequences as functions with domain restricted to positive integers, connecting discrete mathematics to the continuous functions they study elsewhere in Algebra II.
How do sequences appear on the SAT and ACT?
Both the SAT and ACT regularly include sequence problems that test pattern recognition, formula application, and arithmetic progression. Students lose points when they misidentify sequence types or apply the wrong formula under time pressure. SAT questions often embed sequences within real-world contexts, requiring students to recognize arithmetic or geometric patterns in practical situations like compound interest, population growth, or payment schedules. The tests expect fluency with subscript notation and the ability to find specific terms without writing out entire sequences.
ACT math sections frequently ask students to identify the next term in a sequence or determine which formula generates a given pattern. Teachers report that students who practice with varied sequence problems develop the pattern recognition skills needed to quickly categorize problems during timed tests. Strong sequence skills also support success on questions involving exponential functions and logarithms, since geometric sequences directly connect to these topics. College-bound students benefit from automatic recall of sequence formulas, freeing cognitive resources for multi-step problem solving.
Why do students struggle with recursive formulas?
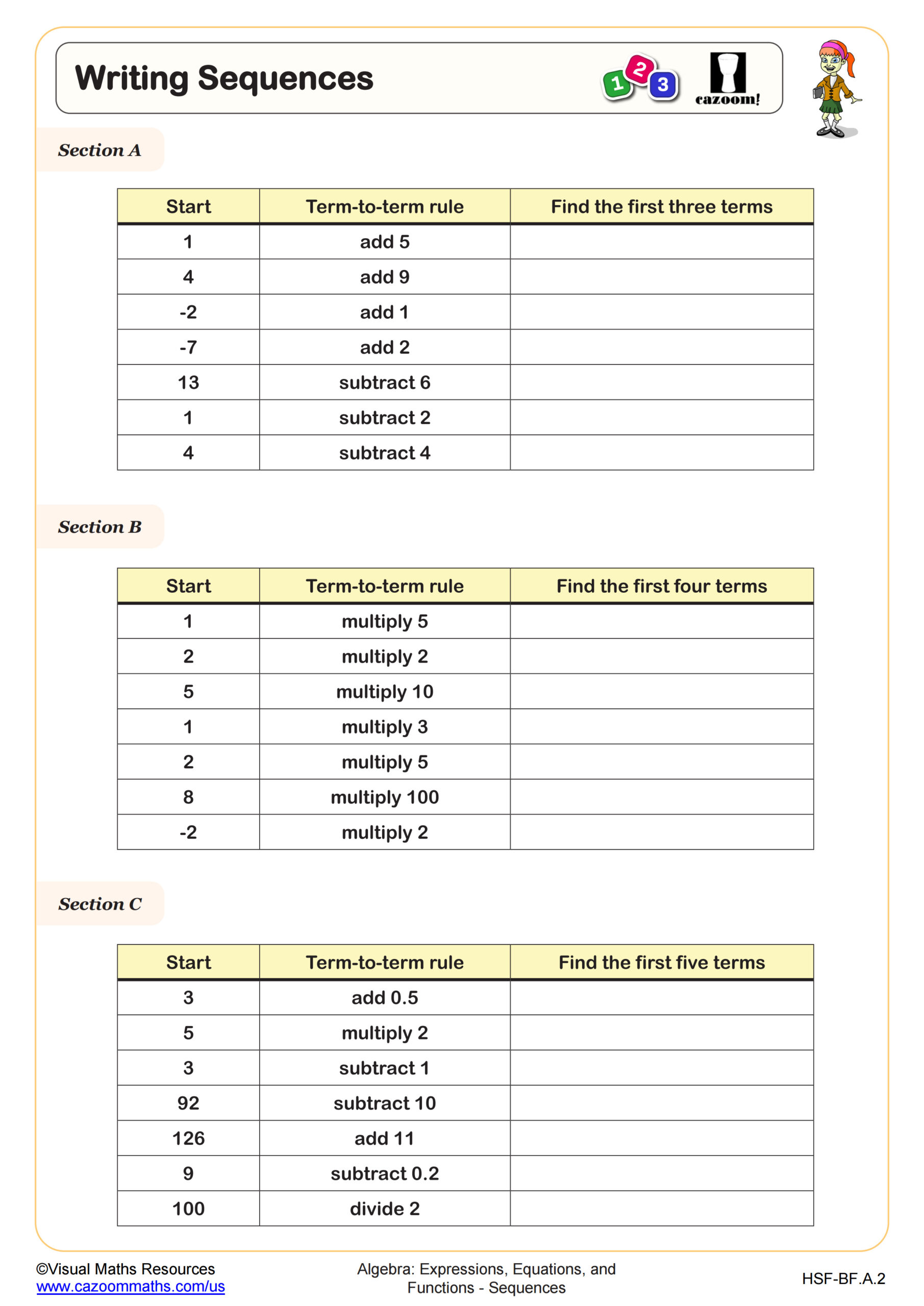
Recursive formulas challenge students because they define terms based on previous terms rather than position alone, requiring a different thinking process than explicit formulas. A common misconception is confusing a_n with a_(n-1), leading students to substitute incorrect values when calculating specific terms. Teachers observe that students confidently tackle recursive problems once they practice building sequence values step-by-step from an initial term. The breakthrough typically happens when students recognize that recursive formulas show relationships between consecutive terms, while explicit formulas calculate any term directly.
This distinction becomes particularly important in computer science and programming, where recursive algorithms form fundamental problem-solving strategies. Students often make the connection between mathematical sequences and coding loops when they see how recursive definitions translate to computational processes. Standardized tests occasionally ask students to convert between recursive and explicit forms, testing deeper understanding beyond formula memorization. Targeted worksheet practice helps students develop comfort with both representations, recognizing when each proves most useful for specific problems.
What strategies help students practice sequences effectively?
Teachers notice that sequenced practice works best when students first identify sequence types before attempting formula manipulation. Starting with pattern recognition exercises where students simply extend sequences builds intuition before introducing formal notation. Students benefit from worksheets that mix arithmetic and geometric sequences, forcing them to analyze each problem rather than applying the same formula repeatedly. Many students lose points on assessments because they rush into calculations without determining whether they're working with addition-based or multiplication-based patterns.
Answer keys prove essential for independent practice because immediate feedback helps students catch notation errors before they become habits. Teachers frequently observe that students who check their work term-by-term develop stronger error detection skills than those who only verify final answers. Worksheets covering special sequences like Fibonacci numbers provide enrichment opportunities for advanced students while reinforcing recursive thinking for all learners. This topic becomes easier when students first master function notation and exponent rules, so reviewing these prerequisite skills alongside sequence practice often accelerates understanding.