Integrated Math 1 Quadratic and Cubic Functions Worksheets
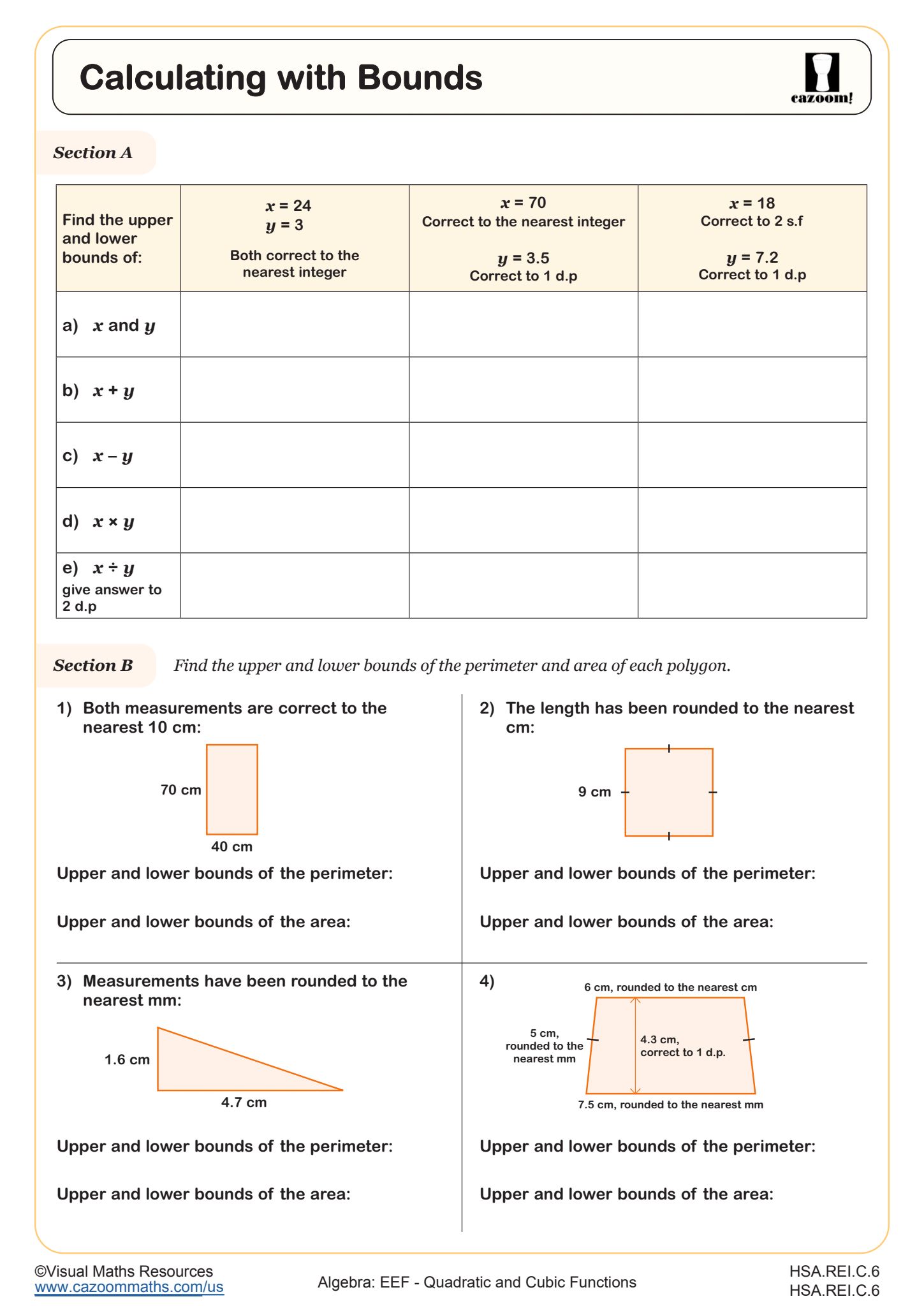
Calculating with Bounds
Completing the Square

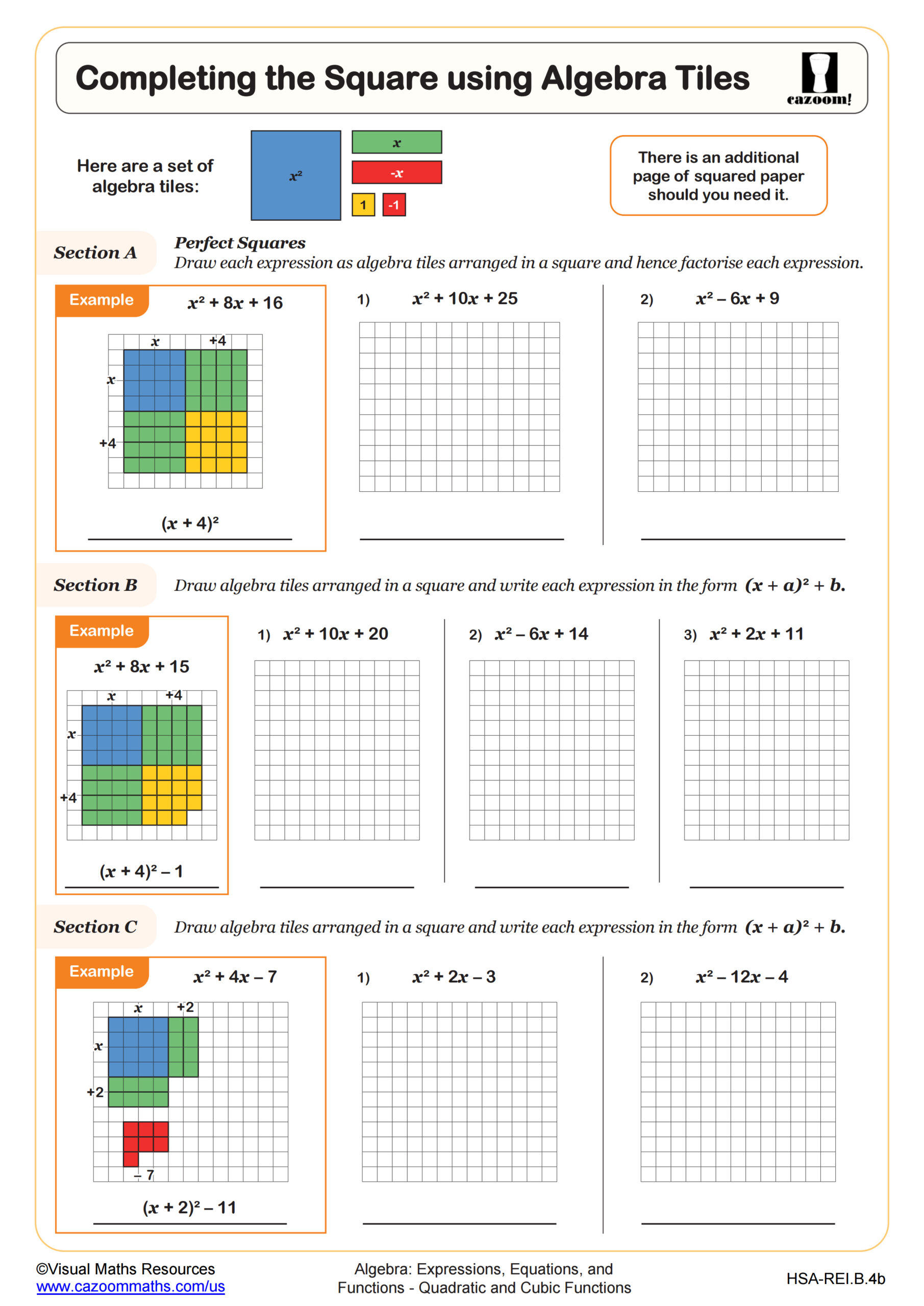
Completing the Square using Algebra Tiles
Factorising Quadratic Expressions - Using the Area Model

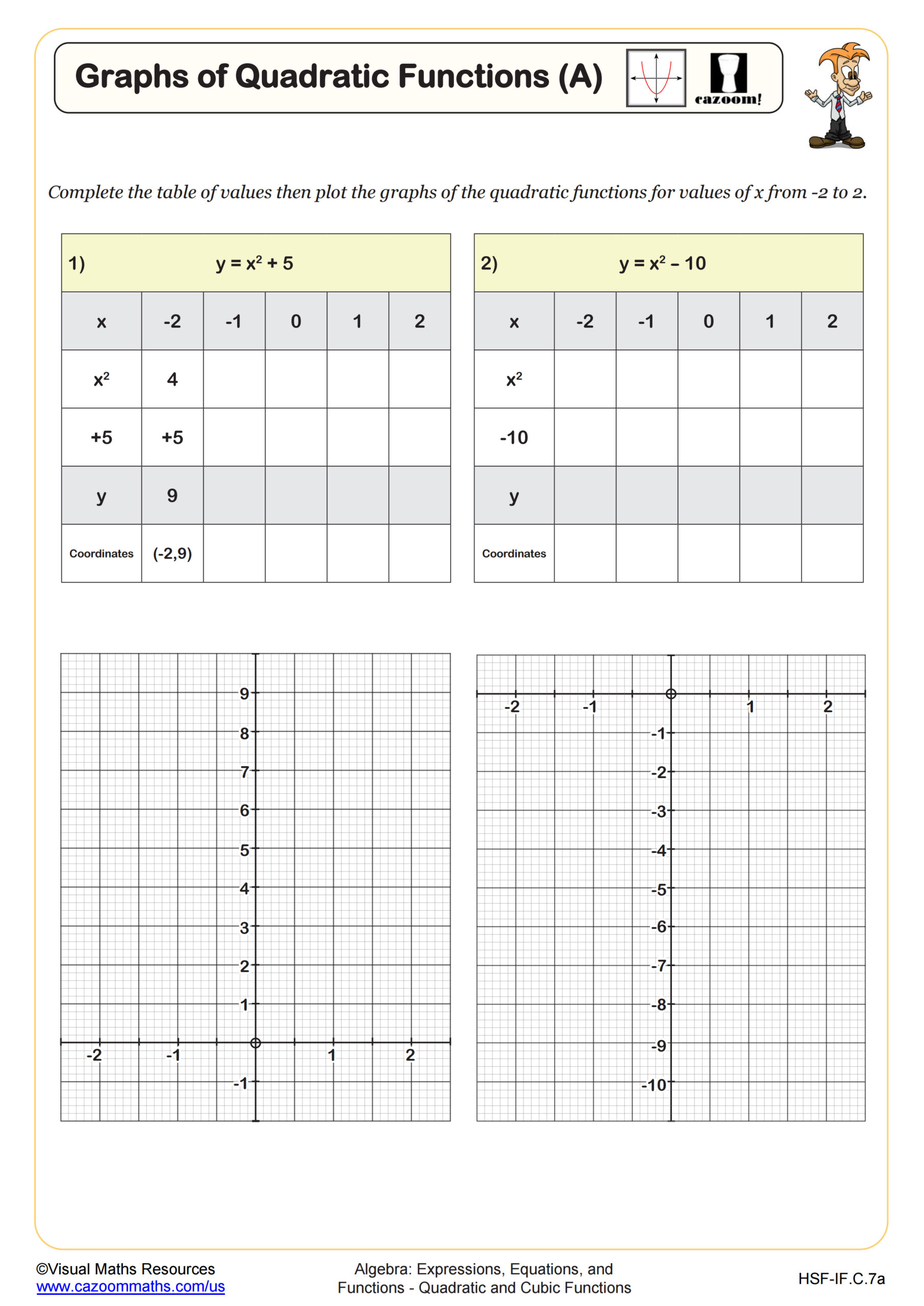
Graphs of Quadratic Functions (A)
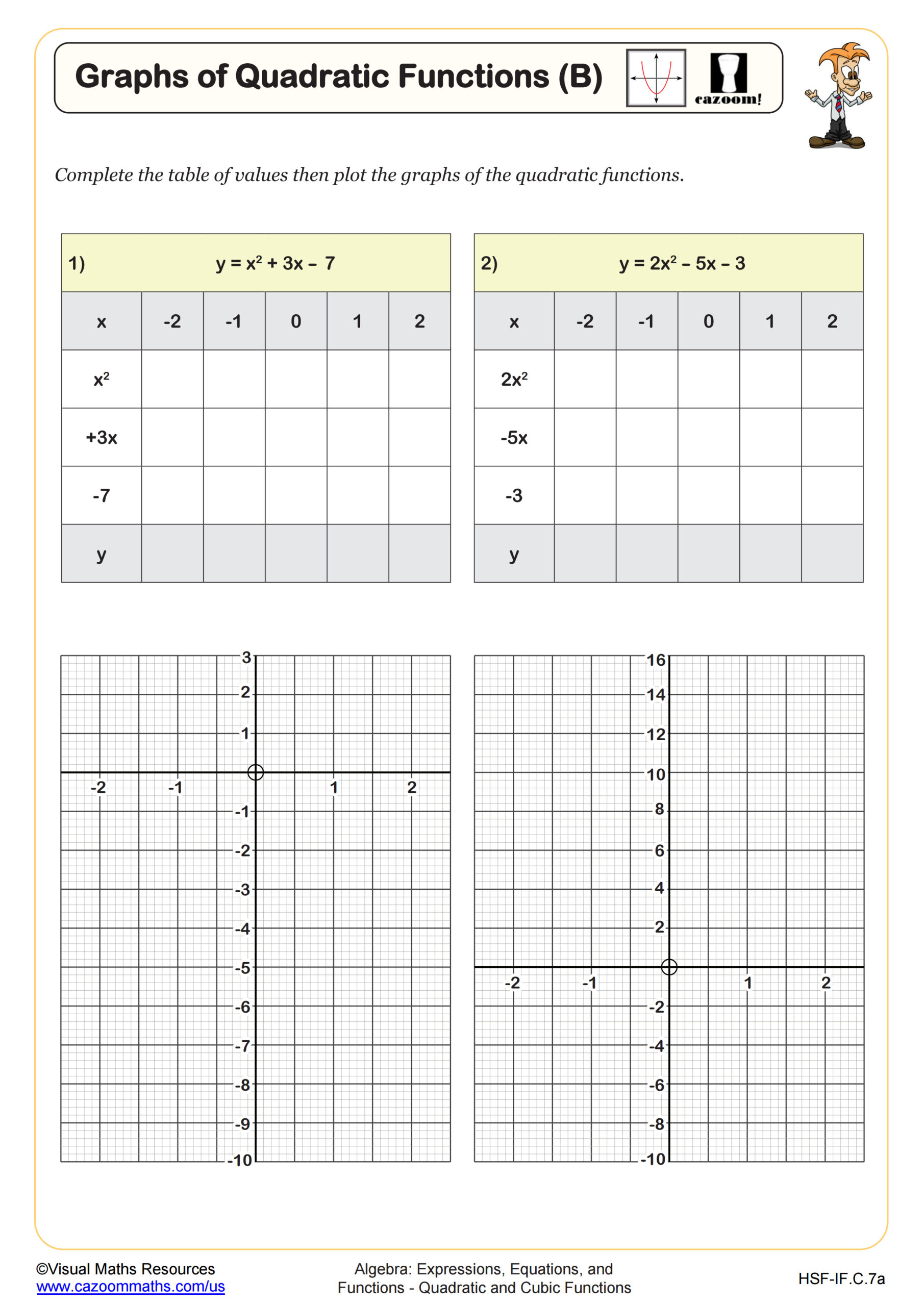
Graphs of Quadratic Functions (B)
Identifying Vertex of Quadratic Functions

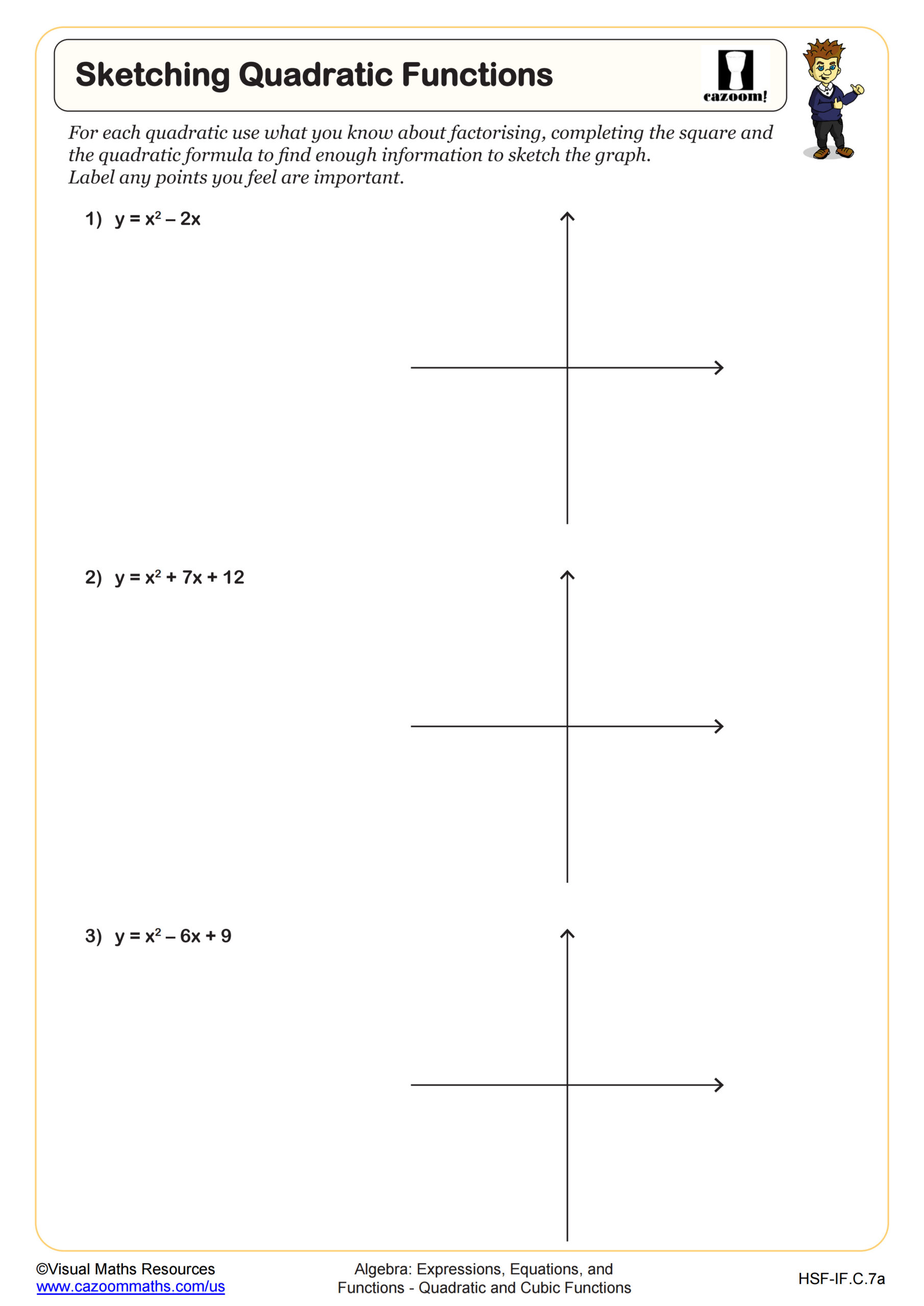
Sketching Quadratic Functions
Solving Linear Simultaneous Equations - Same Coefficients

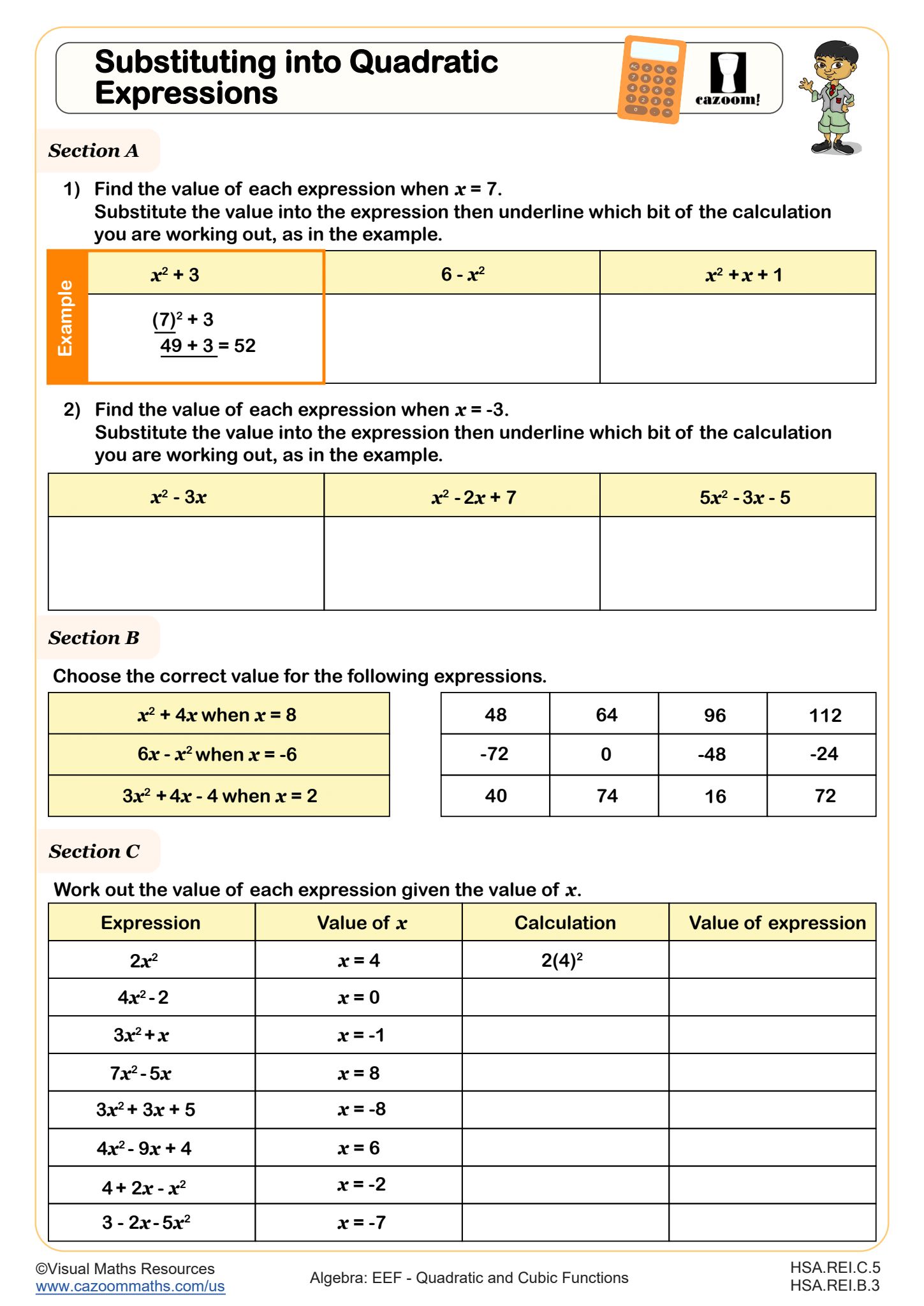
Substituting into Quadratic Expressions
What Topics Are Covered in Integrated Math 1 Quadratic and Cubic Functions?
Integrated Math 1 introduces students to quadratic and cubic functions as they extend their understanding beyond linear relationships. The curriculum covers substituting values into quadratic expressions, factoring quadratic expressions using visual models like area diagrams, completing the square both algebraically and with manipulatives, and solving systems of linear equations. Students learn to recognize parabolic patterns and understand how changing parameters affects function behavior, establishing groundwork for the more advanced function analysis required in Integrated Math 2 and 3.
A common misconception occurs when students attempt to factor quadratic expressions by guessing factor pairs without considering the relationship between the constant term and coefficient of the linear term. Teachers frequently observe students listing all factors of the constant term randomly rather than systematically checking which pair sums to the middle coefficient. The area model addresses this by helping students visualize how the four terms in the expanded form connect to the two binomial factors, making the factoring process more transparent and less reliant on trial and error.
How Do Quadratic and Cubic Functions Appear on Standardized Tests?
The SAT and ACT regularly include questions requiring students to factor quadratic expressions, solve quadratic equations using multiple methods, and interpret parabolic graphs in context. State assessments aligned with Common Core standards expect students to demonstrate understanding of function notation, solve quadratics by factoring or completing the square, and recognize equivalent forms of quadratic expressions. Test questions often embed quadratic relationships within real-world scenarios about projectile motion, area optimization, or revenue modeling, requiring students to translate between verbal descriptions and algebraic representations.
Students lose points when they fail to check their solutions by substituting back into the original equation, especially when solving by completing the square or using the quadratic formula. Another testing pitfall occurs when students correctly factor an expression but forget to set each factor equal to zero to find the actual solutions. Teachers notice that students who practice recognizing perfect square trinomials and common factoring patterns perform more efficiently on timed assessments, as they can quickly identify which solution method will be most direct for a given problem structure.
Why Is Completing the Square Important for Quadratic Functions?
Completing the square transforms a quadratic expression from standard form into vertex form, revealing the parabola's maximum or minimum point and making transformations visible. This technique requires students to recognize perfect square trinomials and understand how to create them by adding a strategic constant term. While factoring works only for quadratics with rational roots, completing the square applies universally and develops the conceptual foundation students need for deriving the quadratic formula in Integrated Math 2. Algebra tiles provide a concrete representation of this process, helping students visualize why adding the square of half the linear coefficient creates a perfect square trinomial.
This skill connects directly to physics and engineering applications where finding maximum height or minimum cost matters. Completing the square allows students to determine when a launched object reaches its peak height or identify the dimensions that minimize material costs for a fixed area. College-bound STEM students encounter this technique repeatedly in calculus when analyzing optimization problems and in statistics when working with least-squares regression. Understanding why the process works, not just memorizing steps, helps students apply the method flexibly across disciplines.
How Can Teachers Use These Worksheets in Integrated Math 1 Classrooms?
The worksheets scaffold learning by starting with substitution into quadratic expressions before progressing to more complex procedures like completing the square and factoring. Visual approaches using area models and algebra tiles provide entry points for students who struggle with abstract algebraic manipulation, while traditional algebraic methods appear on separate worksheets for students ready for symbolic reasoning. The included answer keys allow teachers to quickly assess student understanding and identify whether errors stem from arithmetic mistakes or conceptual gaps about quadratic structure.
Many teachers use these worksheets for differentiated practice during unit instruction, assigning different problem sets based on student readiness levels. The substitution worksheets work well as warm-up activities to reinforce function notation before introducing new solving techniques. Teachers preparing students for state assessments often use the factoring and completing the square worksheets as timed practice to build procedural fluency. The worksheets also support intervention work for students who need additional practice with specific techniques, and paired work where students compare solution methods helps deepen understanding of when each approach is most efficient.