Integrated Math 3 Quadratic and Cubic Functions Worksheets
What Do Students Learn About Quadratic and Cubic Functions in Integrated Math 3?
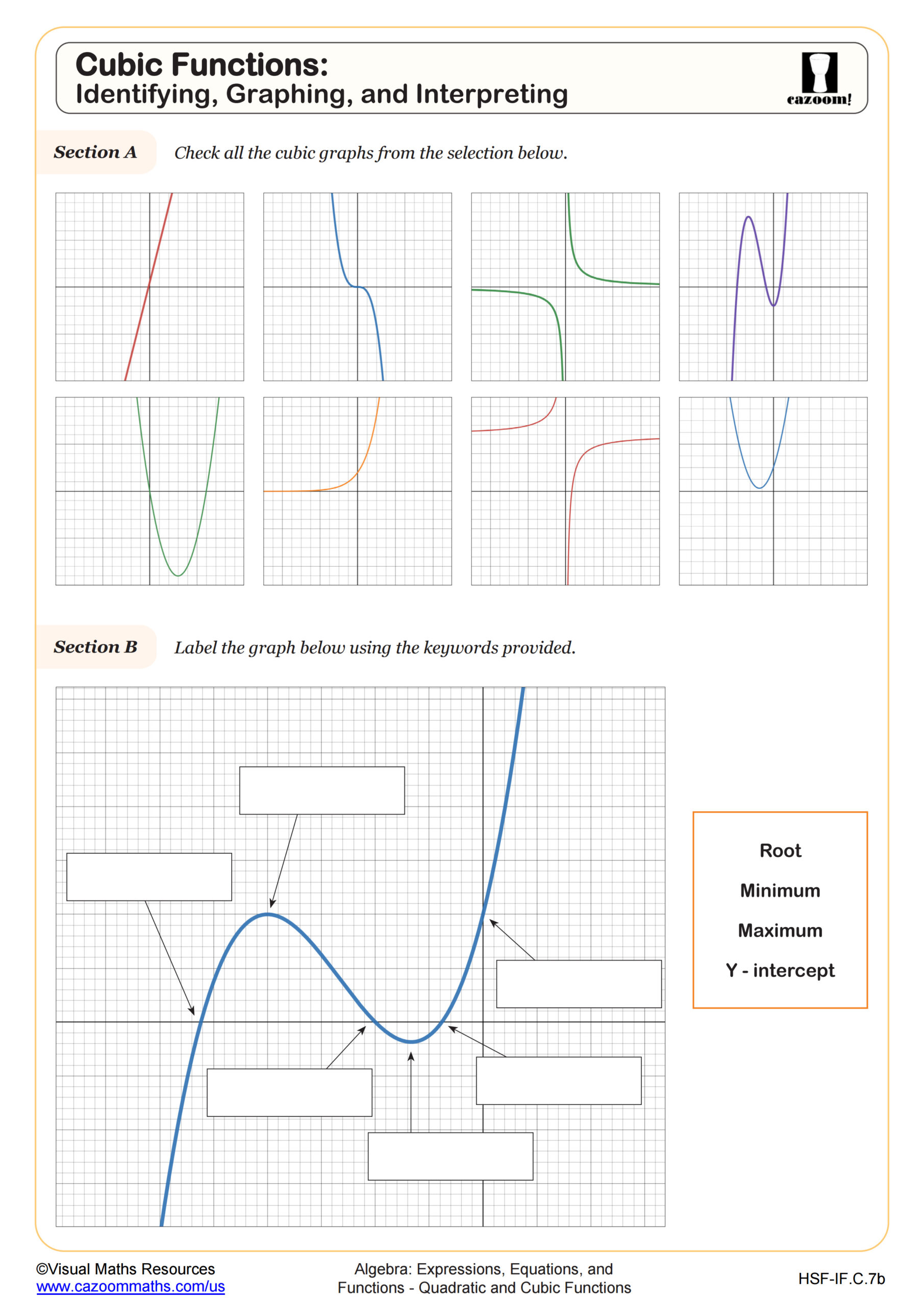
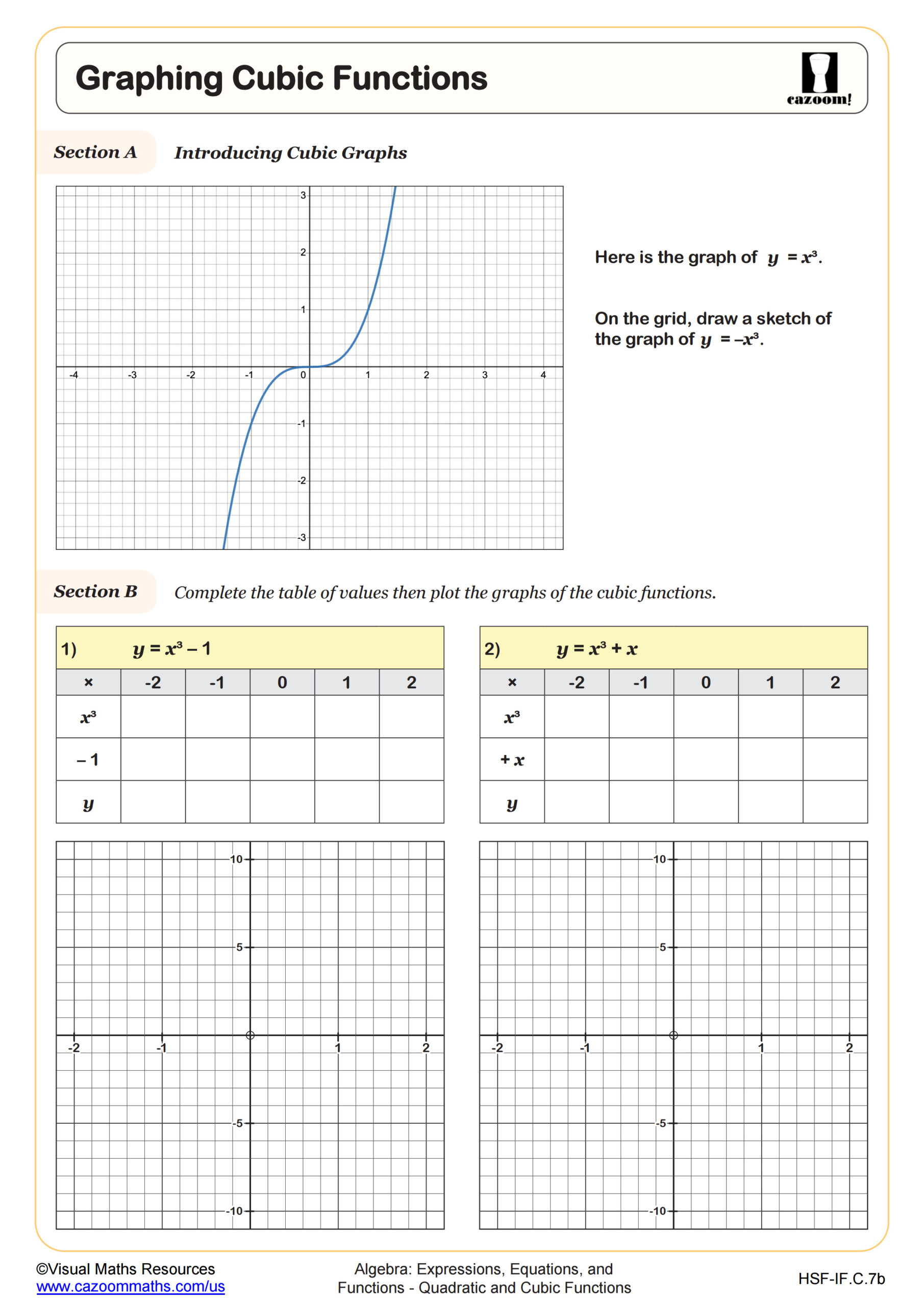
Students extend their quadratic function knowledge to include cubic functions, focusing on graphing both function types and understanding how transformations affect their graphs. The curriculum emphasizes identifying key features such as vertex and axis of symmetry for quadratics, and inflection points and local extrema for cubics. Students also analyze how horizontal and vertical translations, reflections, and stretches alter the parent functions y = x² and y = x³.
A common error occurs when students apply quadratic symmetry properties to cubic functions. Many students expect cubic graphs to have a vertical line of symmetry like parabolas, leading to incorrect sketches. Teachers find success by having students create function tables for y = x³ to observe that while the function has point symmetry about the origin, it lacks the line symmetry of quadratics. Recognizing this distinction helps students graph cubics accurately and understand why transformation rules apply uniformly despite different symmetry properties.
How Do Quadratic and Cubic Functions Appear on the SAT and ACT?
Standardized tests like the SAT and ACT assess quadratic and cubic functions through multiple-choice and grid-in questions that require students to match equations to graphs, identify transformations, or determine key features from an equation. The SAT calculator section frequently includes questions where students must recognize how changing parameters in f(x) = a(x - h)³ + k affects the graph's position or shape. Questions may also ask students to identify which graph represents a given cubic equation or determine the number of real zeros from a graph.
Students lose points when they confuse the direction of horizontal translations, particularly the counterintuitive h value in (x - h). Many also struggle to distinguish between cubic and quadratic graphs when both are presented as answer choices, especially when the viewing window shows limited end behavior. Teachers notice that students who practice matching symbolic and graphical representations perform significantly better on these assessment items than those who rely solely on memorized transformation rules.
How Do Transformations Apply to Both Quadratic and Cubic Functions?
Transformations follow consistent rules across function families, making the parent function approach efficient for graphing. For both y = x² and y = x³, the general form f(x) = a(x - h)ⁿ + k reveals how to shift and stretch the graph. The parameter h moves the graph horizontally (opposite sign), k shifts it vertically (same sign), and a controls vertical stretch and reflection. Students who master these patterns with quadratics can immediately apply them to cubics and other function types they'll encounter in precalculus.
This skill connects directly to physics and engineering applications where cubic functions model volume relationships and structural stress. When designing packaging, the volume of a box formed by cutting squares from a sheet depends on a cubic function of the cut size. Engineers analyzing beam deflection also work with cubic models. College-bound STEM students encounter these functions in calculus when studying polynomial behavior, making fluency with transformations a foundational skill for higher mathematics.
How Can Teachers Use These Quadratic and Cubic Functions Worksheets in Integrated Math 3?
The worksheets provide structured practice that moves from identifying function characteristics to graphing and interpreting transformations, supporting the gradual release model many Integrated Math 3 teachers use. Each worksheet includes varied problem types that require students to work between multiple representations: equations, graphs, and verbal descriptions. The answer keys allow students to check their work independently during practice sessions, helping them catch conceptual errors before assessments rather than repeating mistakes.
Teachers use these worksheets effectively as warm-up review before introducing rational functions, as intervention materials for students who struggled with quadratic concepts earlier in the year, or as homework assignments that reinforce classroom instruction. Paired work sessions where students compare their graphing approaches often reveal misconceptions about transformation notation. The worksheets also serve as targeted SAT preparation since function transformation questions appear regularly on the calculator-permitted section, and students benefit from repeated exposure to matching equations with their corresponding graphs.