Ratio Worksheets

At Cazoom Math we offer a huge range of ratio worksheets to help children understand this topic. Ratios are used in many aspects of our everyday lives so our question sheets reflect that, allowing children to practice their knowledge with problems involving exchange rates and worded questions. We have ratio worksheets suitable for all levels and abilities, from simplest form equivalent ratios up to more complex ratio problems. Our ratio worksheets contain engaging activities which make the topic of ratios entertaining and enjoyable, and our ratios worksheets are all supplied with answers to check how well your child or pupil is doing.

Best Value for Money - the Unitary Method

Grades: 6th Grade, 7th Grade

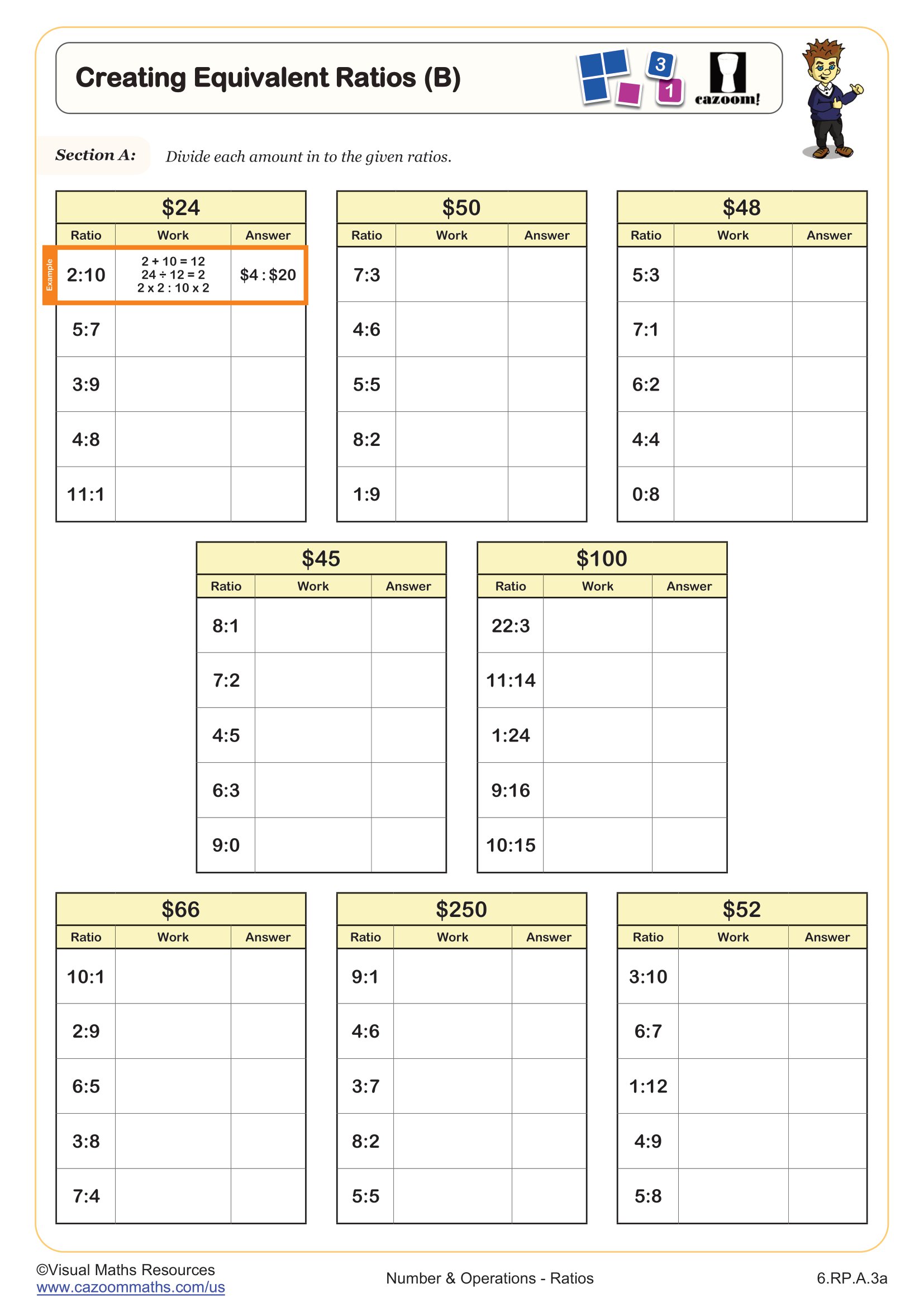
Creating Equivalent Ratios (B)

Grades: 6th Grade

$Preview of Creating Equivalent Ratios (B)$

Direct Proportion (A)

Grades: 6th Grade, Geometry, IM 1

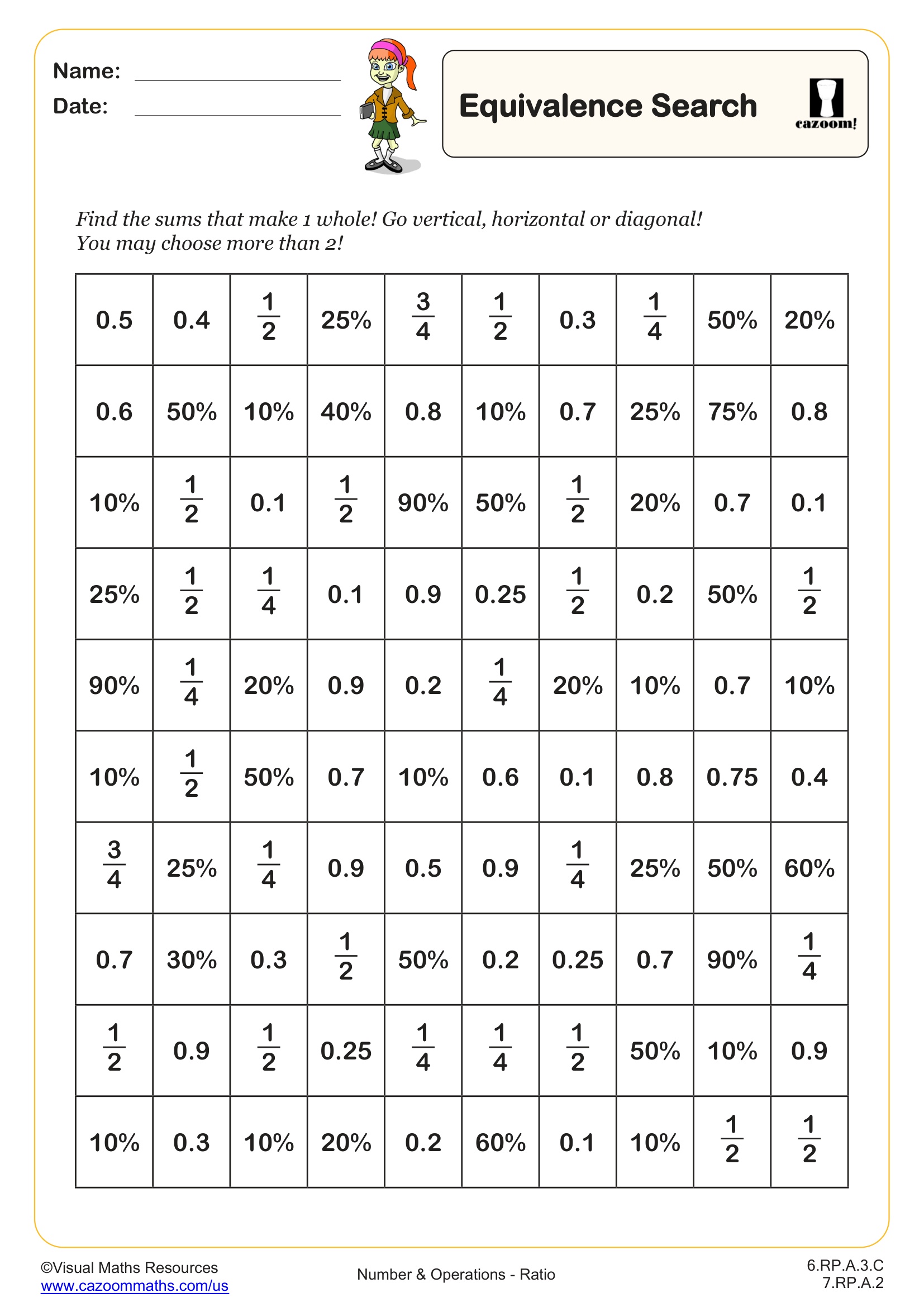
Equivalence Search (A)

Grades: 6th Grade, 7th Grade

Exchange Rates

Grades: 6th Grade, 7th Grade

Fraction, Percentage and Ratio Problems

Grades: 6th Grade, 7th Grade

Introducing Ratio

Grades: 6th Grade, 7th Grade

Ratio - Difference Known

Grades: 6th Grade, 7th Grade

$Preview of Ratio - Difference Known$

Ratio - Using Bar Models (A)

Grades: 6th Grade

Ratio - Using Bar Models (B)

Grades: 6th Grade

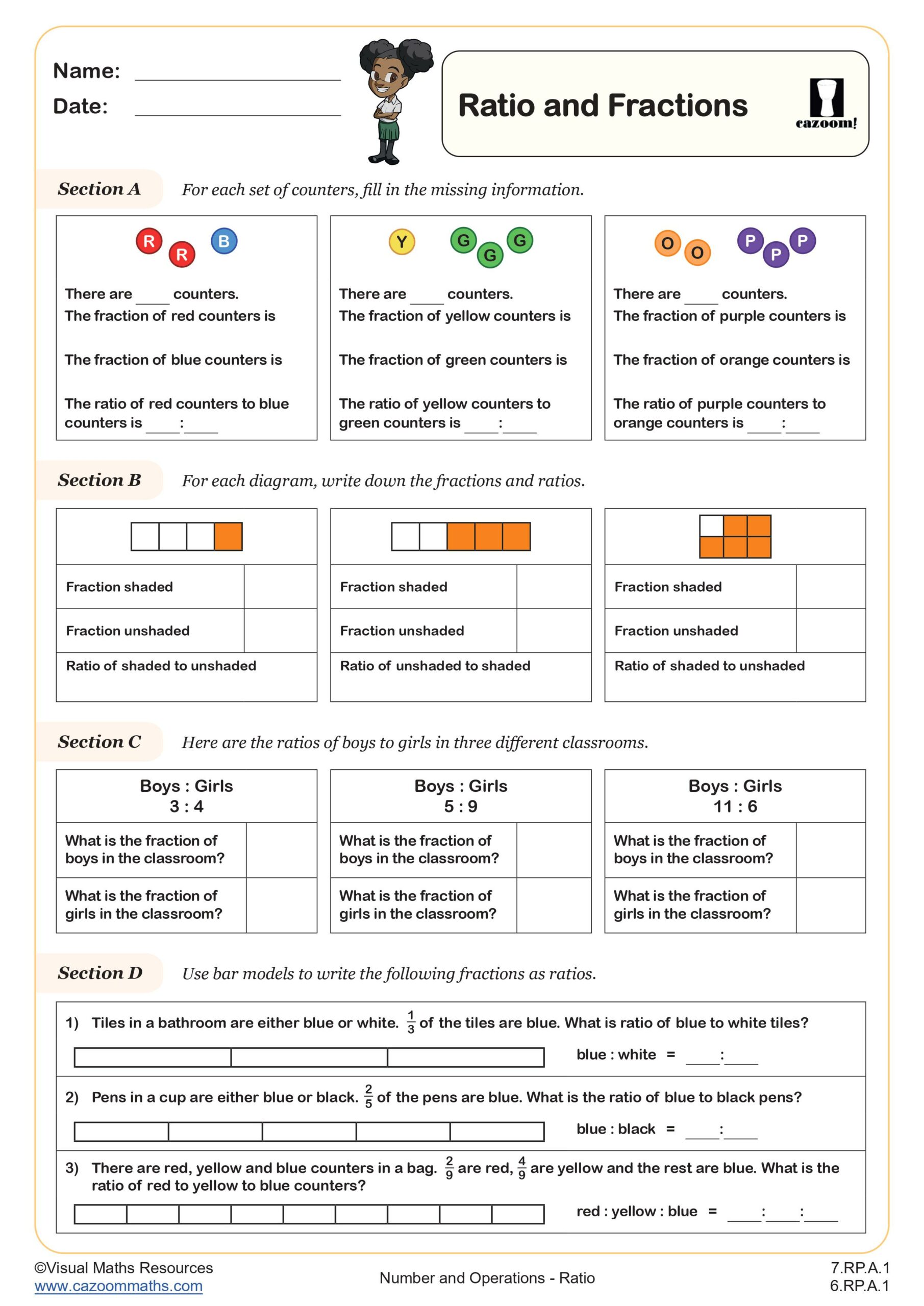
Ratio and Fractions

Grades: 6th Grade, 7th Grade

Ratio Reasoning Problems (A)

Grades: 6th Grade, 7th Grade

Ratio Reasoning Problems (B)

Grades: 6th Grade, 7th Grade

Ratio- One Amount Known

Grades: 6th Grade, 7th Grade

$Preview of Ratio- One Amount Known$

Ratios 1:n and n:1

Grades: 6th Grade, 7th Grade

Ratios and Proportions Synthesis

Grades: 6th Grade, 7th Grade

Representing Ratios with Tape Diagrams

Grades: 6th Grade, 7th Grade

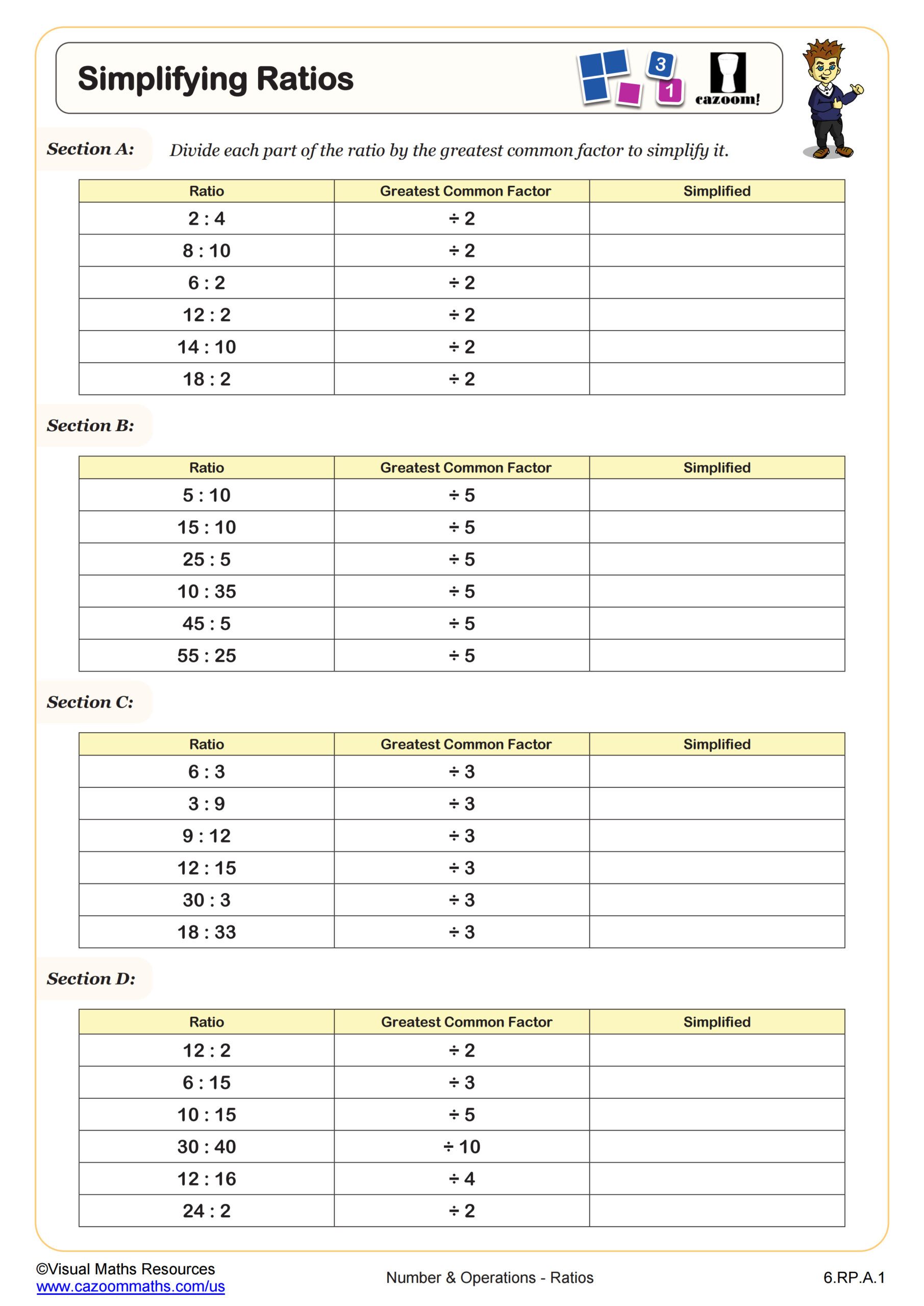
Simplifying Ratios

Grades: 6th Grade

Using Ratio Notation

Grades: 6th Grade, 7th Grade

Writing Ratios (A)

Grades: 6th Grade

Writing Ratios (B)

Grades: 6th Grade

Changing Ratios

Grades: 7th Grade

$Preview of Changing Ratios$

Creating Equivalent Ratios (A)

Grades: 7th Grade

Drawing Conversion Graphs

Grades: 7th Grade, 8th Grade

$Preview of Drawing Conversion Graphs$

Express One Number as a Percentage of Another

Grades: 7th Grade

Factory and Worker Proportion Problems

Grades: 7th Grade, Algebra I, IM 1

Forming Equations from Ratios (A)

Grades: 7th Grade, Algebra I

$Preview of Forming Equations from Ratios (A)$

Ratios and Coordinates

Grades: Geometry, IM 1

DOWNLOAD PDF RATIO WORKSHEETS

Our ratio worksheets are available to download and print, and can either be used in the classroom or to support children’s learning at home.

We have worksheets available to cover all aspects of ratios in the curriculum. Our ratio worksheets present all the information they need to know in a concise, easy to understand format and provide plenty of opportunities to apply their knowledge. Using Cazoom Math’s ratio worksheets will help boost students’ confidence at using ratios and prepare them for any ratio problem they might come across.

Explanation of Ratios

Ratios are used in many aspects of our everyday lives.

They tell us that two variables are proportional to each other, and are used in cooking, gambling, currency exchange and more. For this reason, it is important to make sure students have a thorough understanding of this topic by using ratio worksheets.

The Everyday Uses of Ratios

It is highly likely that you will be using and calculating ratios in your everyday life without even realizing it.

When following a recipe, the ingredients will all be proportional to each other. So, if you are baking a cake the recipe advises using 100g of butter and 300g of flour, the ratio between those two ingredients is 1:3. Knowing this ratio, you can easily scale the amounts of ingredients up or down to adapt to the quantity of cake required, ensuring that the end product will still be the same quality and consistency.

Application of Ratios

In scientific disciplines, particularly chemistry, ratios are extremely important.

Different substances can react in different ways depending on the ratio of one to another, so it could potentially pose a safety risk if researchers did not use proper ratios. If there is too much of one substance in a mixture, toxic gases could be released, so they must understand how ratios work and measure carefully according to this proportion.

What is equivalent ratio?

If two ratios when simplified have the same value, they are called equivalent ratios. Basically, equivalent ratios make the same comparison of numbers, and can be expressed as a multiple of the other.

Examples of equivalent ratios:

1 : 2 : 4 : 8 : 16

10 : 20 : 40 : 80

0,25 : 0,5 : 1:2