High School Quadratic and Cubic Functions Worksheets

Cazoom Math High School Quadratic and Cubic Functions Worksheets provide students with a structured environment to practice polynomial behavior through multiple practice exercises. US curriculum experts created the materials to assist teachers and parents who teach high school algebra to their students. The materials begin with basic parabola drawing methods before progressing to more complex cubic transformation exercises. The worksheets teach students essential analytical abilities, which will help them succeed in calculus. Students learn to perform algebraic operations on these functions while gaining comprehension of their graphical representation. Students develop their confidence through a structured practice system, which provides them with multiple opportunities to solve various problem types. The worksheets serve to establish connections between fundamental algebra concepts and sophisticated mathematical operations. Students discover through these materials that polynomial functions serve as mathematical representations that model real-world problems in physical and economic systems. The materials follow the standard mathematical content requirements for high school education throughout the United States.

Calculating with Bounds

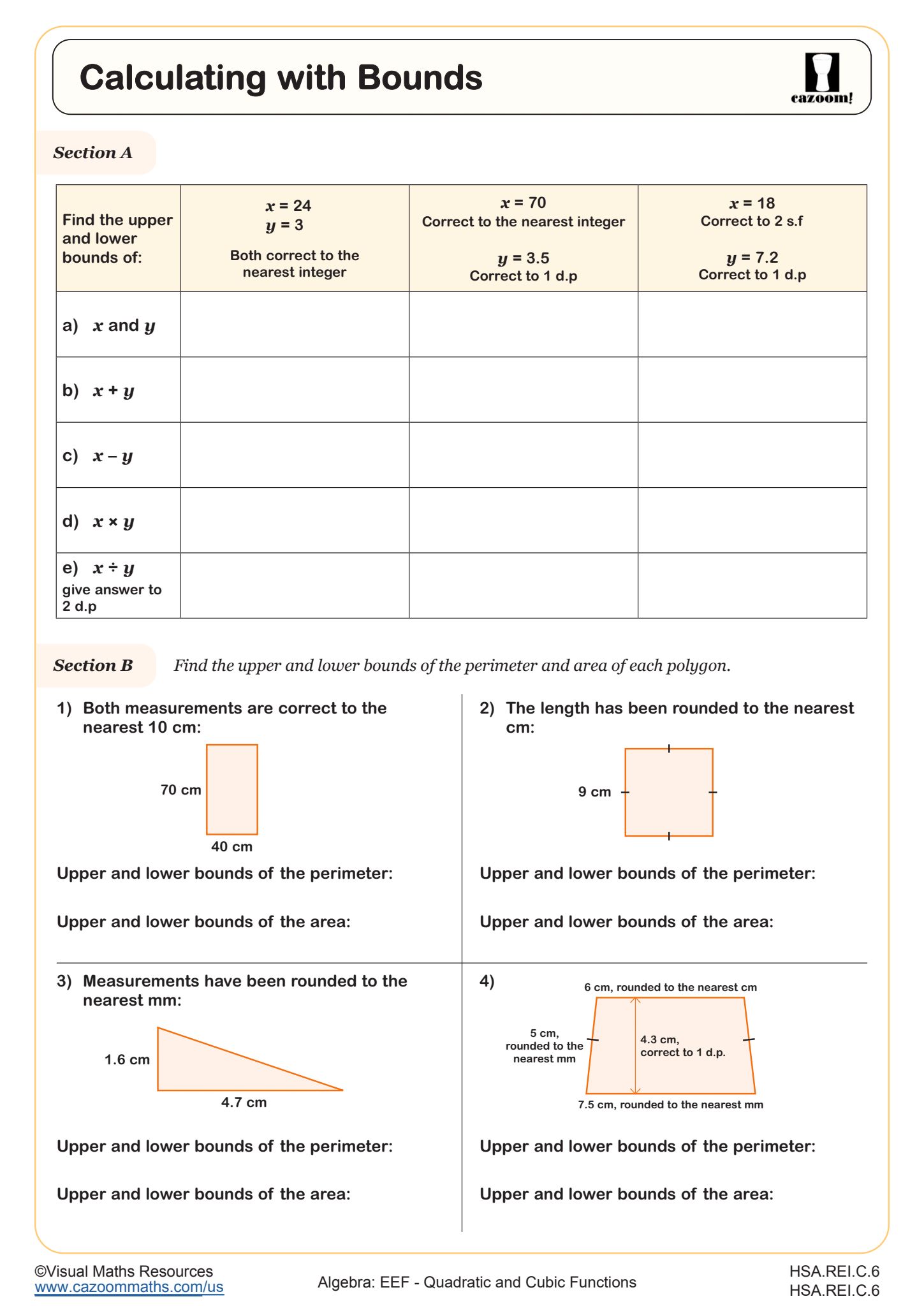
$Preview of Calculating with Bounds$

Completing the Square

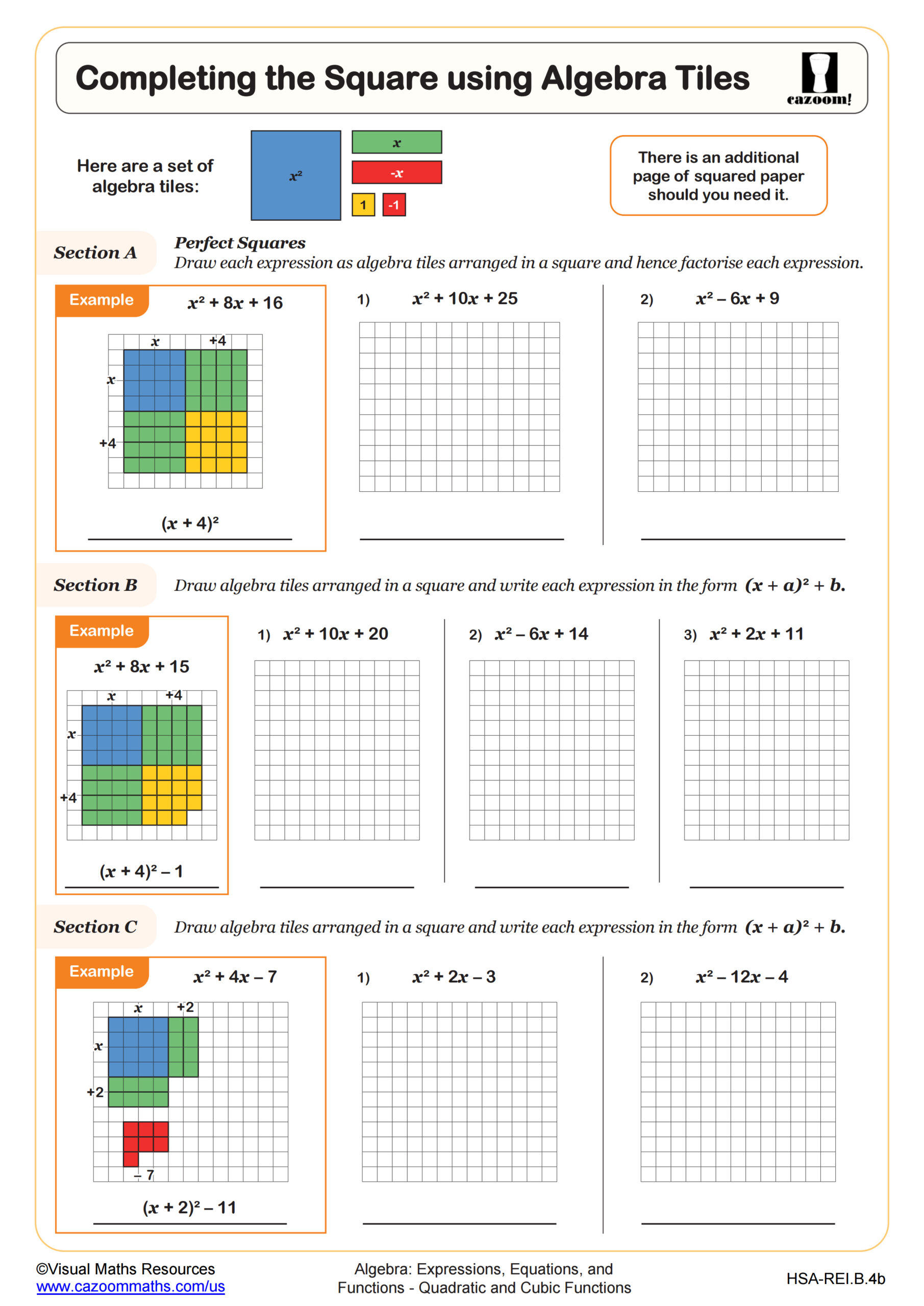
Completing the Square using Algebra Tiles

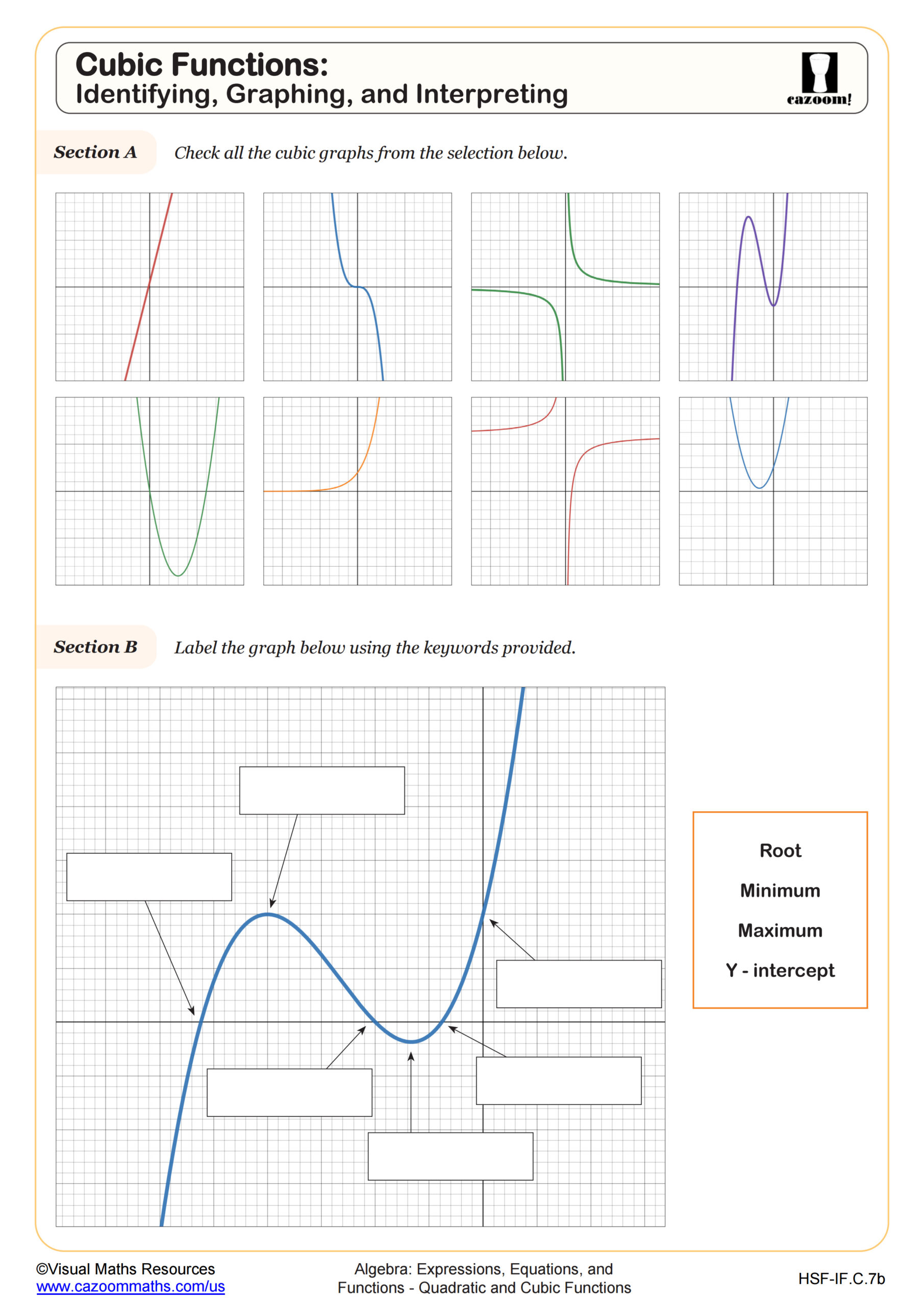
Cubic Functions: Identifying, Graphing, and Interpreting

Factorising Quadratic Expressions - Using the Area Model

$Preview of Factorising Quadratic Expressions - Using the Area Model$

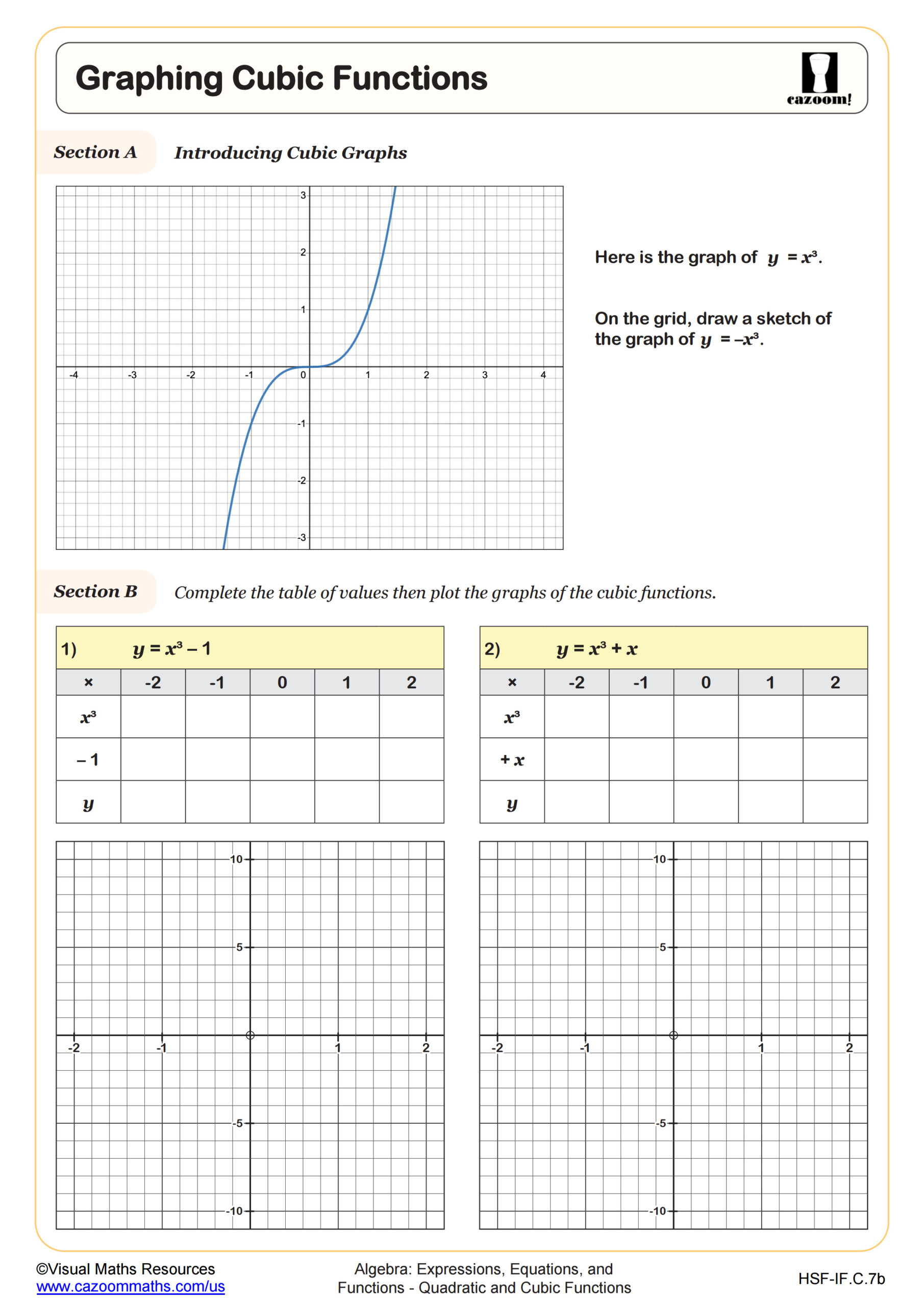
Graphing Cubic Functions

Graphs of Quadratic Functions (A)

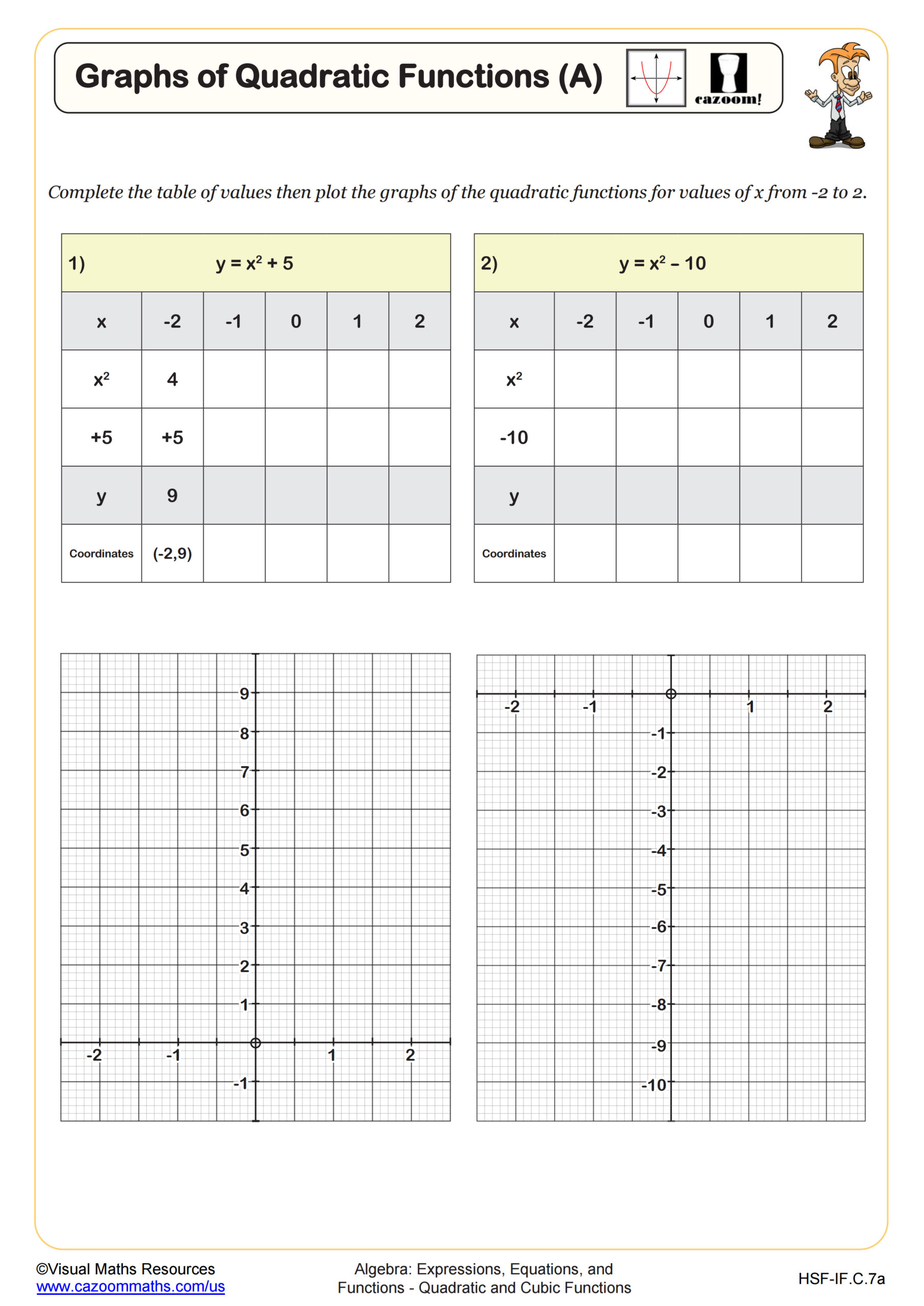
Graphs of Quadratic Functions (B)

Identifying Vertex of Quadratic Functions

Quadratic Expressions and Equations Involving Areas

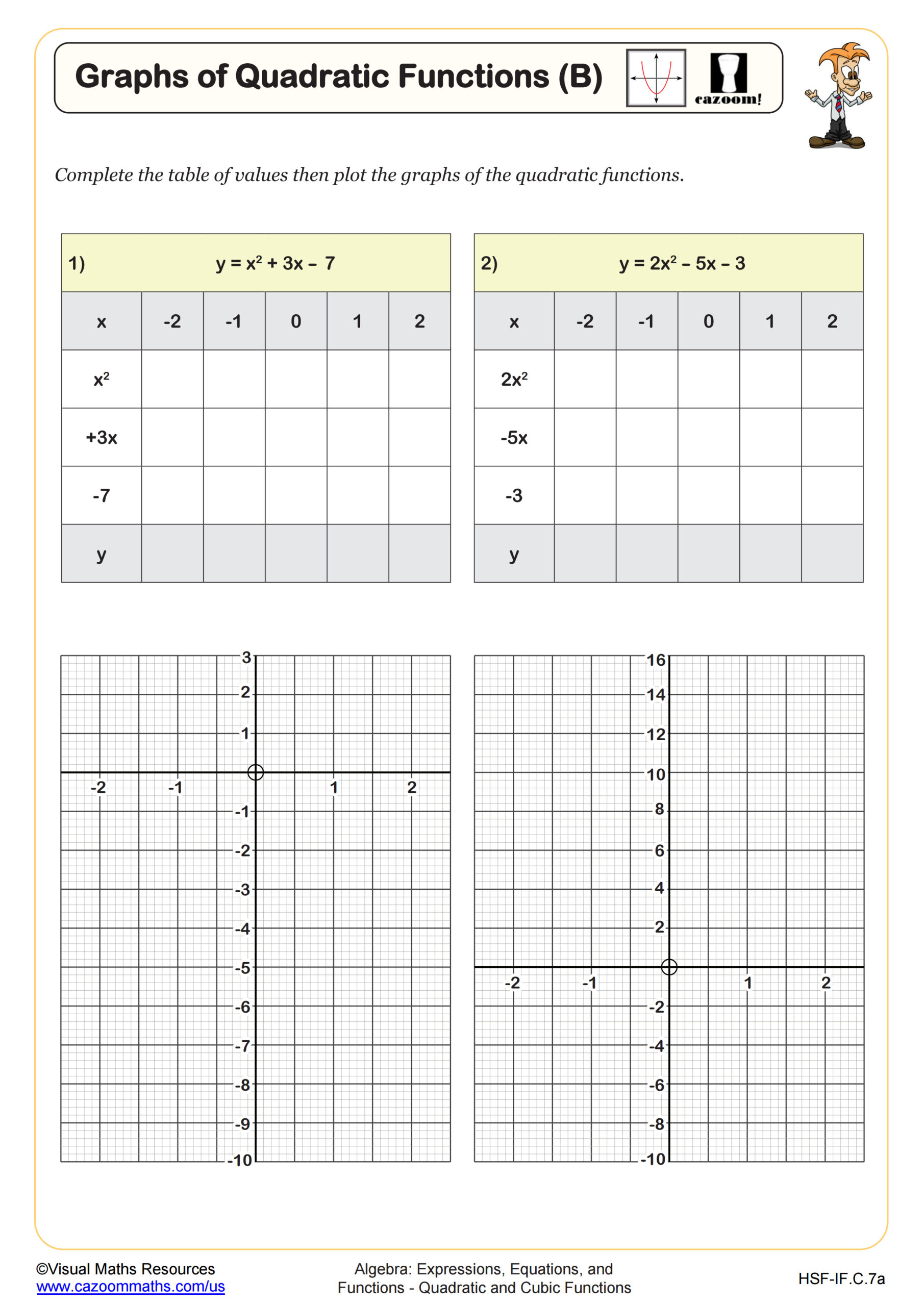
$Preview of Quadratic Expressions and Equations Involving Areas$

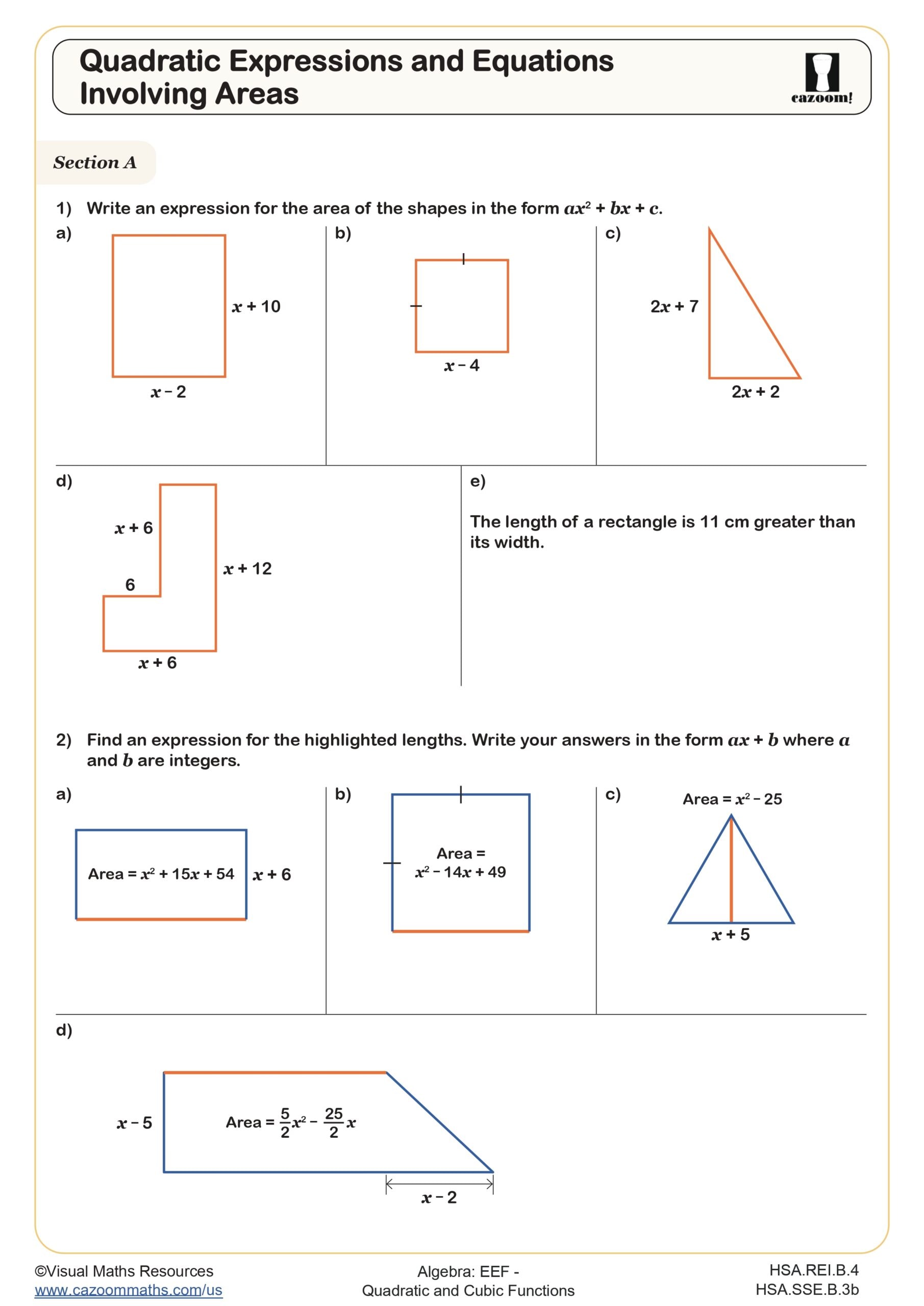
Sketching Quadratic Functions

Solving Linear Simultaneous Equations - Same Coefficients

$Preview of Solving Linear Simultaneous Equations - Same Coefficients$

Substituting into Quadratic Expressions

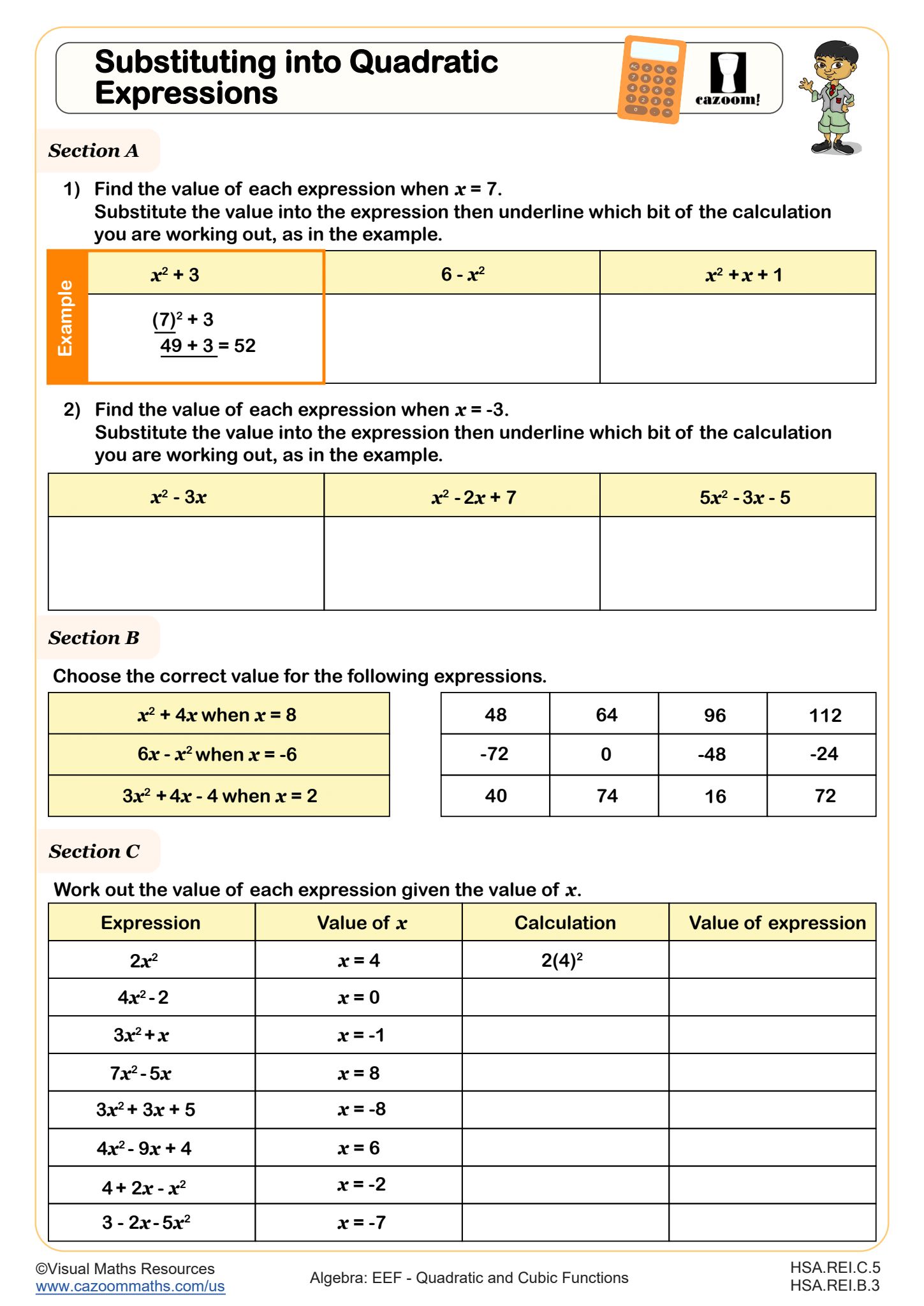
$Preview of Substituting into Quadratic Expressions$

Translations of Non-Linear Graphs

Why These Printable PDFs High School Quadratic and Cubic Functions Activities Make Exam Prep Easier

These worksheets directly connect to the linear functions that students mastered in earlier grades. They practice recognizing how parabolas and cubic curves behave differently from straight lines. Students discover patterns between algebraic forms and their corresponding graphs. This builds intuition about polynomial behavior before encountering derivatives.

Regular practice with these functions prepares students for the topics of trigonometry and exponential functions ahead. They develop flexibility in choosing factoring, completing the square, or graphing approaches. Working through varied problems trains students to match techniques to specific situations. This strategic thinking becomes essential for rational functions and logarithms.

What’s Included? Calculating with Bounds, Cubic Functions, Factorising Quadratic Expressions and More

These worksheets take students from numeric substitution to graphical representation and finally to abstract algebraic manipulation. Learners begin by substituting values into quadratic expressions before advancing to completing the square and sketching parabolas. Each worksheet includes complete, worked examples demonstrating each stage of reasoning. Covering factoring, graphing, cubic behavior, and applied quadratic problems, this collection helps students connect algebraic structure to visual patterns and real-world contexts.

Are You Teaching Quadratic and Cubic Functions the Best Way? Try These Cazoom Math Algebra Resources

Teachers appreciate how these worksheets fit directly into lesson planning without modification. The graduated difficulty levels let instructors differentiate instruction across student abilities simultaneously. Quick starter problems begin lessons, while extension questions challenge advanced learners. Solution keys reveal complete reasoning pathways, making it straightforward to identify misconceptions.

The structured progression saves grading time through clear solution formats. Teachers effectively deploy these sheets for homework, classwork, and review sessions. A variety of problems prevent memorization of patterns while reinforcing conceptual understanding. Many educators find that students grasp vertex form and factoring methods more quickly when using these materials. The worksheets adapt easily to both individual practice and collaborative group work.

From Sports to Weather Predictions: Where These Skills Show Up in Real Life

Students encounter numerous real-world applications of quadratic and cubic functions that extend beyond their schoolwork. The equations help engineers determine how loads distribute throughout structures. The supply and demand curves in economics help economists determine market equilibrium points. Game developers utilize polynomial functions to create realistic motion physics in their games.

•Calculating projectile paths in sports

•Designing suspension bridge tensions

•Modeling bacteria growth rates

•Creating animation movement paths