Inequalities Worksheets
Inequalities on a Number Line
Year groups: 7, 8

Solving Inequalities (A)
Year groups: 7, 8

Forming and Solving Linear Inequalities
Year groups: 8, 9

Solving Inequalities (B)
Year groups: 8, 9

Solving Inequalities with Two Inequality Signs
Year groups: 8, 9

Graphing Inequalities (A)
Year groups: 10, 11
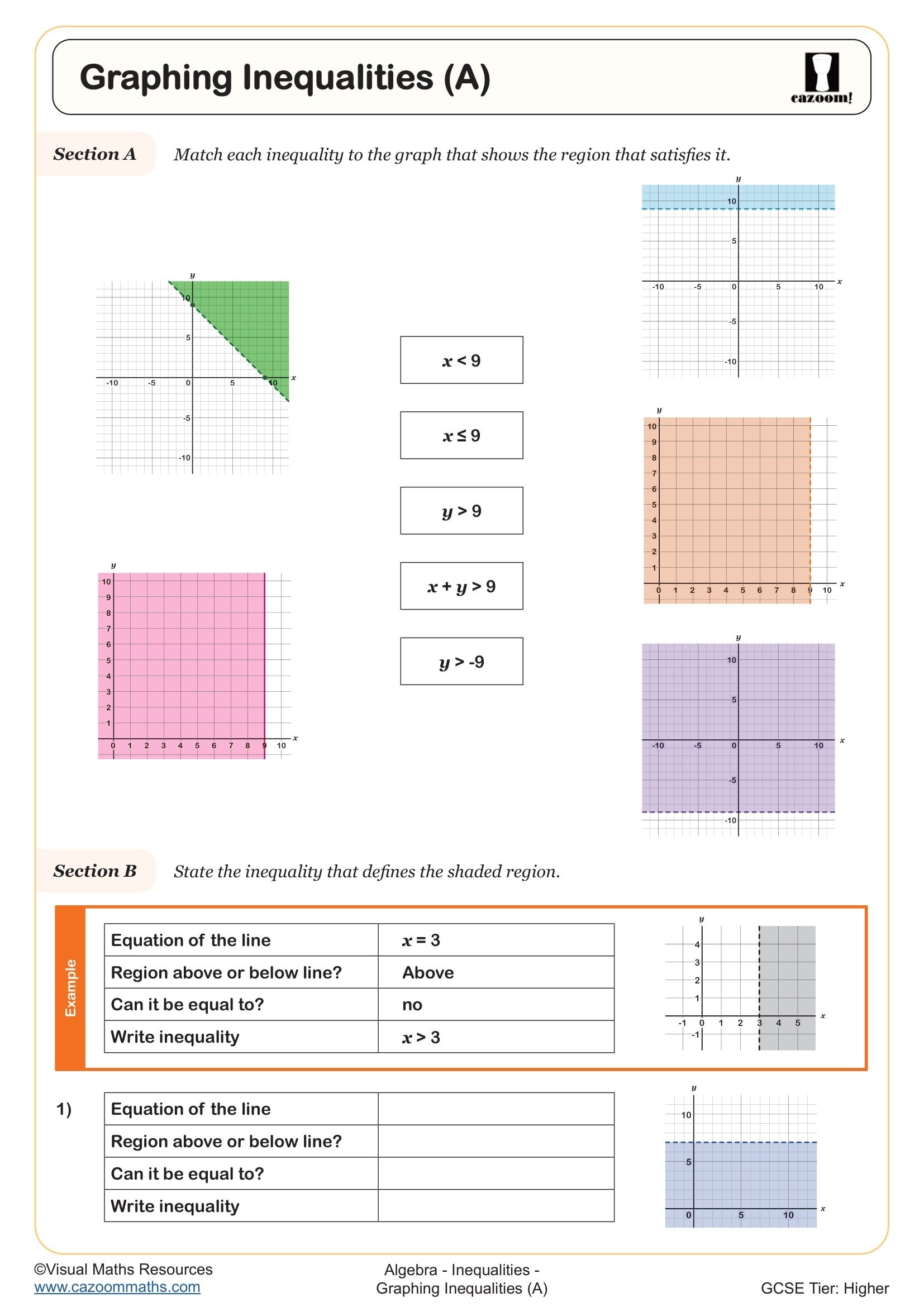
Graphing Inequalities (B)
Year groups: 10, 11
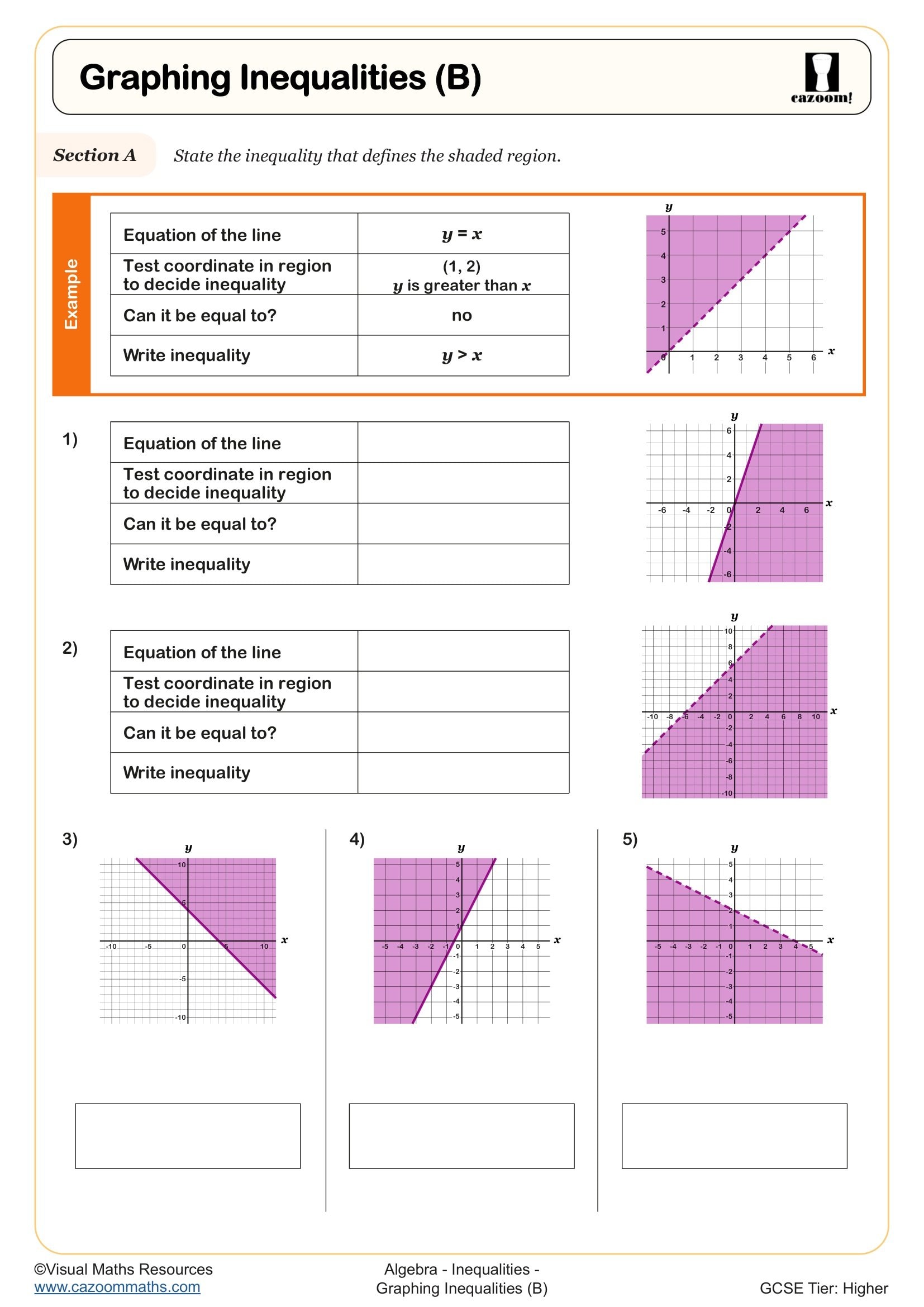
Graphing Inequalities (C)
Year groups: 10, 11
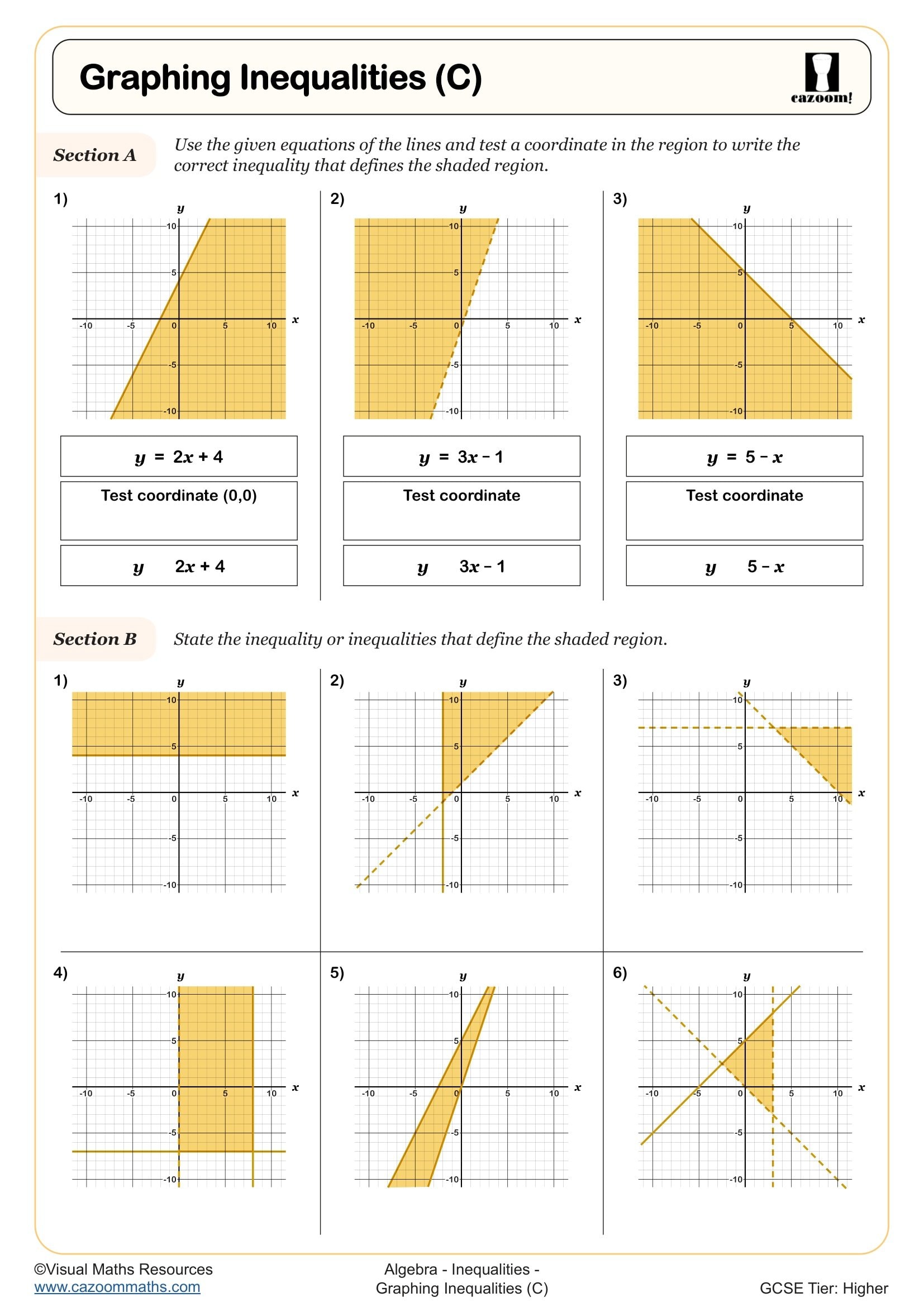
Shading Regions (A)
Year groups: 10, 11
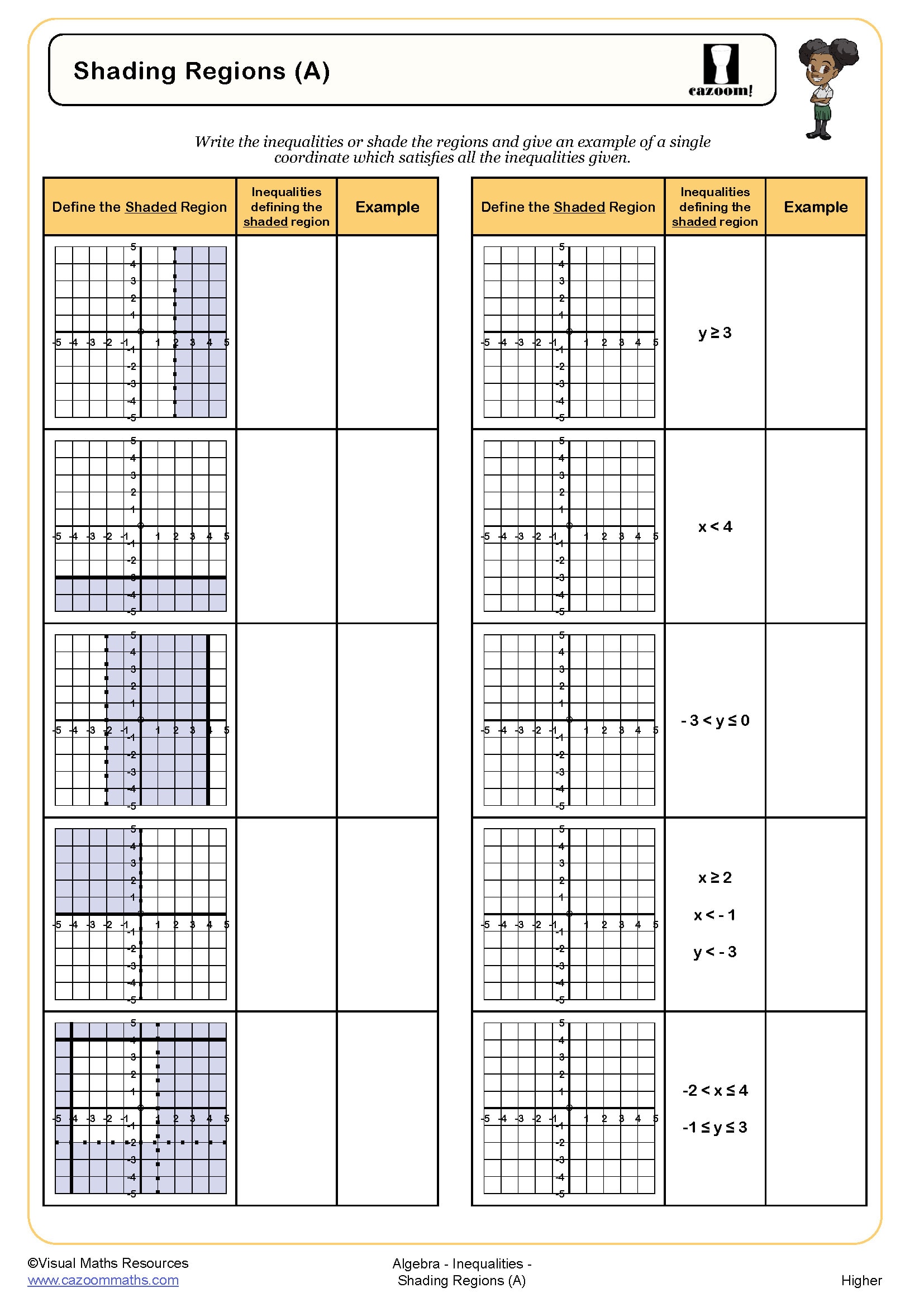
Shading Regions (B)
Year groups: 10, 11
Solving Quadratic Inequalities (A) - without sketching
Year groups: 10, 11
-without-sketching-Questions.jpg?w=3840)
Solving Quadratic Inequalities (B)
Year groups: 10, 11
-Worksheet.jpg?w=3840)
Solving Quadratic Inequalities (C) - satisfying two inequalities
Year groups: 10, 11
-satisfying-two-inequalities-Worksheet.jpg?w=3840)
All worksheets are created by the team of experienced teachers at Cazoom Maths.
PRINTABLE SOLVING INEQUALITIES WORKSHEETS WITH ANSWERS PDF
Check out our downloadable indices worksheets pdf, which will improve your student’s knowledge of various mathematical calculations related to indices such as—solving a mathematical inequality, one-step inequalities, properties of inequalities, and many more related concepts. These worksheets are created in easy-to-download PDF format, and include solutions, and are designed to help your students better understand this complex concept of maths. These worksheets are excellent resources that will make learning fun and exciting, helping your students to be able to recognise and solve various critical functions related to inequalities.
Understanding The Concept Of Inequalities
Inequalities are akin to a seesaw at the playground, where there are unequal numbers on both sides of the balance. Suppose you were to establish who may play on each end of the see-saw. This is an inequality. In other words, this is how we measure different numbers against each other as in one group may have up to 10 children while the other can only have less than but not more than 10 children. Maths has inequalities which inform us about such things as; is the one value bigger or smaller than another or not equal? However, unlike stating that two things are exactly the same, inequalities admit discrepancies between them. For example, think about them as being open to numbers that belong to a certain set and I mean it allows many numbers at once not just one number. Therefore, if you see something like x≥5 it’s talking about x being any number that is 5 and above i.e. included in this particular group which also includes five itself.
Properties Of Inequalities
Inequalities have their own set of rules, a bit like guidelines that help keep numbers in check. One key property is that if you add or take away the same amount from both sides, the inequality still holds true. For instance, if you have £5 more than your friend, and you both spend £2, you’ll still have £5 more. Also, if you multiply or divide both sides by a positive number, the direction of the inequality won’t change. However, and here’s a clever twist, if you multiply or divide by a negative number, the inequality flips over—think of it as a dance move where everything spins to the opposite direction. These properties make sure that even when numbers move around, we can track how they stand in relation to each other, keeping the playground fair and fun.
Using Inequalities In Real Life
In real life, we use inequalities all the time, often without even realising it. Say you’re saving up to buy a bike and you know it costs no more than £200. You’re dealing with an inequality because the amount you need can be less than or equal to £200, but not a penny more. Or, if you’re baking and the recipe says to cook at 180°C or higher to get a crispy top, that’s also an inequality; your oven’s temperature can go above 180°C but not below. Inequalities help us with decisions like figuring out how much money we can spend on groceries if we need to keep under a certain budget or deciding the speed we can drive without going over the speed limit. They’re handy maths tools that apply to everyday choices, ensuring we stay within limits and meet certain conditions to get through our day.