Year 10 Solving Equations Worksheets

Year 10 Solving Equations Worksheets created by UK curriculum experts provide comprehensive practice for GCSE-level algebraic techniques. These carefully structured resources help secondary students master equation-solving methods through progressive difficulty levels whilst building essential mathematical reasoning skills. Teachers and parents use these worksheets to support classroom learning, exam preparation, and independent study, ensuring students develop the algebraic fluency required for GCSE success and beyond. By incorporating real-world contexts alongside abstract problems, these materials demonstrate the practical relevance of algebraic thinking, motivating students to engage deeply with challenging content. Each worksheet balances accessibility with rigour, allowing learners to progress at their own pace whilst maintaining high mathematical standards expected at this crucial stage of secondary education.

Algebraic Angles in Parallel Lines

Find the Values

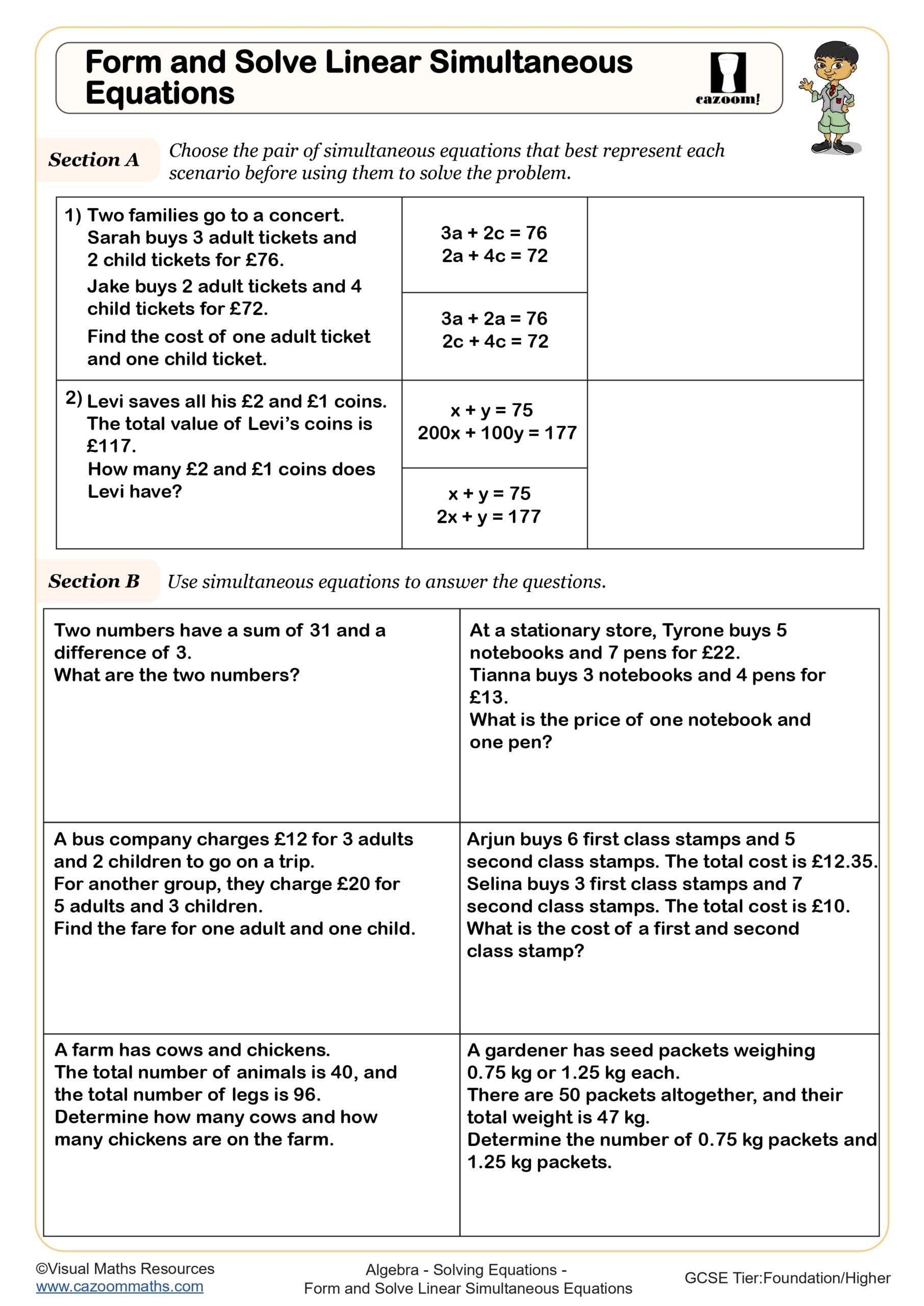
Form and Solve Linear Simultaneous Equations

Forming and Solving Equations

Forming and Solving Equations involving Angles

Forming and Solving Linear Equations: a𝑥 = b and 𝑥/a = b

Forming and Solving Linear Equations: x + a = b and x - a = b

Forming and Solving Quadratic Equations

I Think of A Number Problems

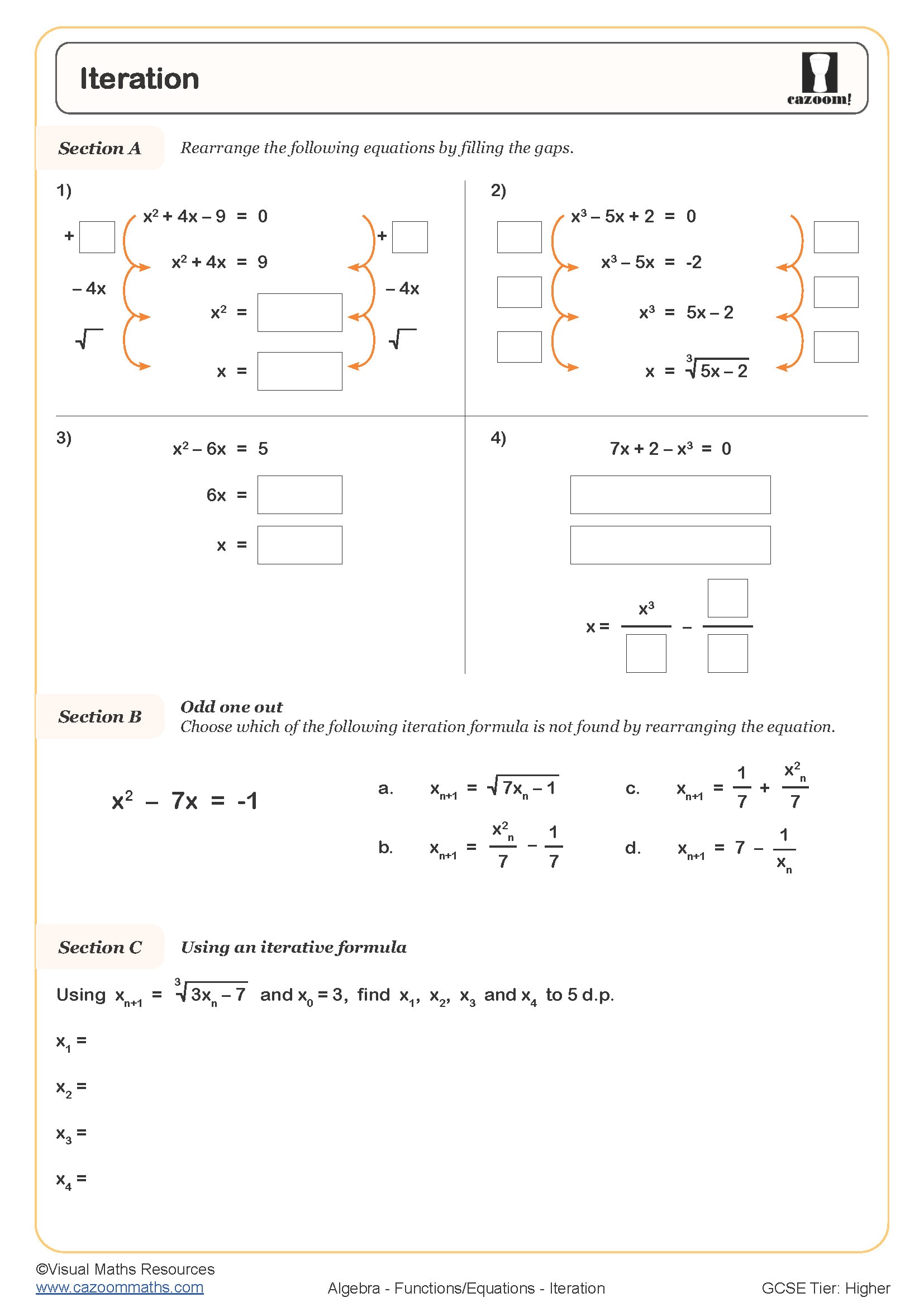
Iteration

Manipulating Equations

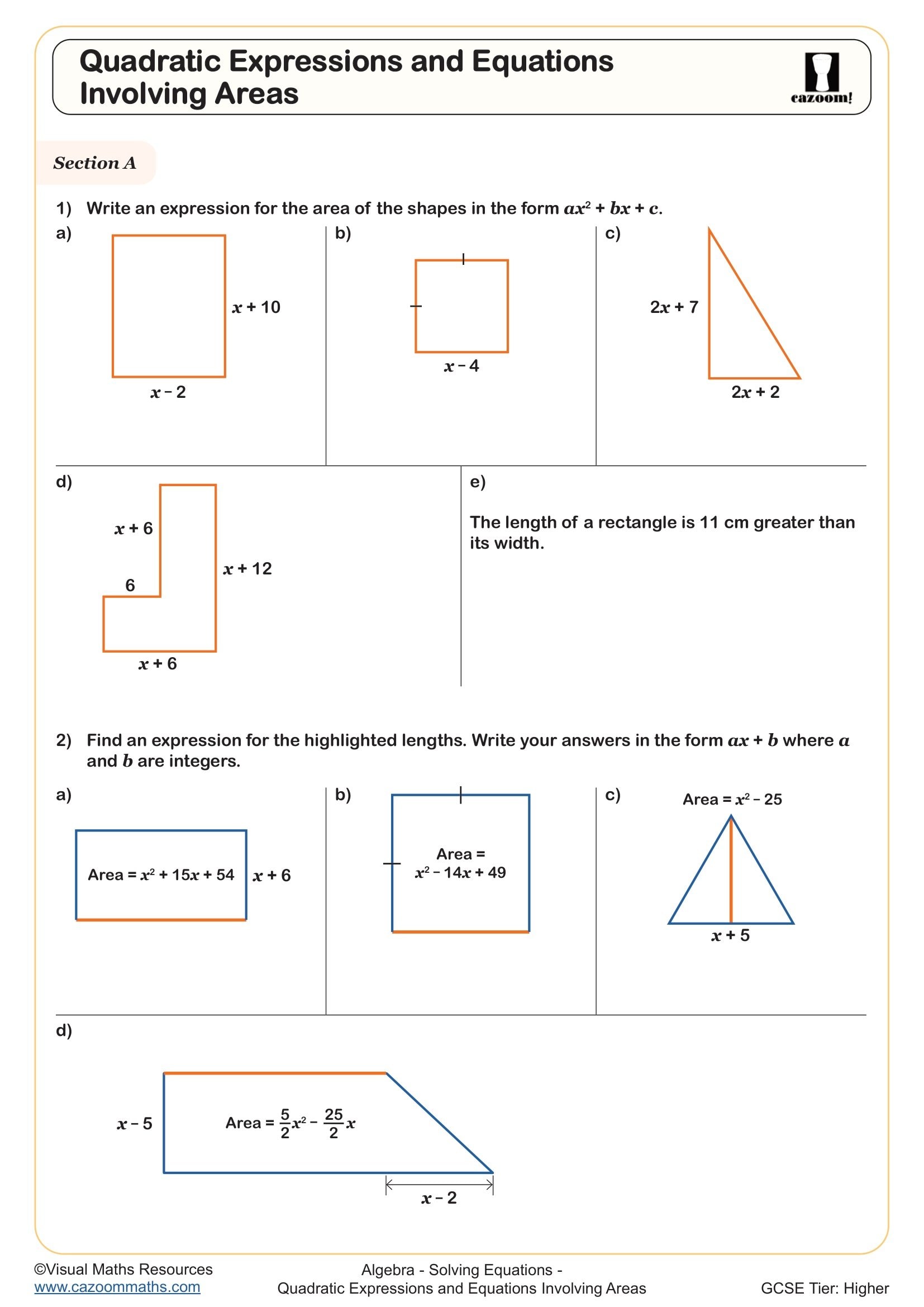
Quadratic Expressions and Equations Involving Areas

Solving Equations - Unknowns are Indices

Solving Equations - Unknowns on Both Sides

Solving Equations 15 Minute Challenge (A)

Solving Equations 15 Minute Challenge (B)

Solving Equations Involving Area of Rectangles

Solving Equations Involving Brackets

Solving Equations Involving Fractions

Solving Equations with Algebraic Perimeters

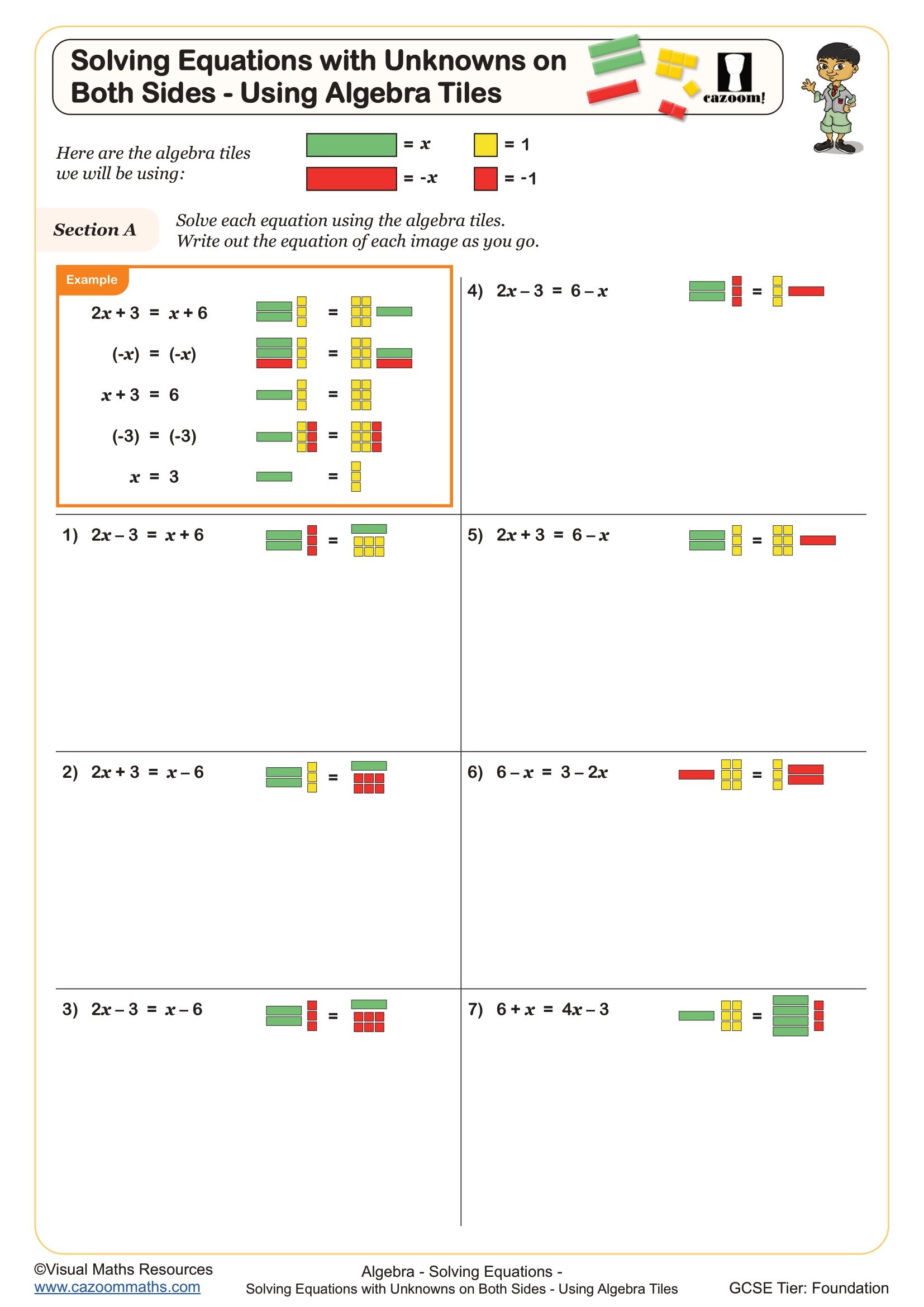
Solving Equations with Unknowns on Both Sides - Using Algebra Tiles

Solving Linear Equations (A)

Solving Linear Equations (B)

Solving Linear Equations (C)

Solving Linear Equations (D)

Solving Linear Simultaneous Equations

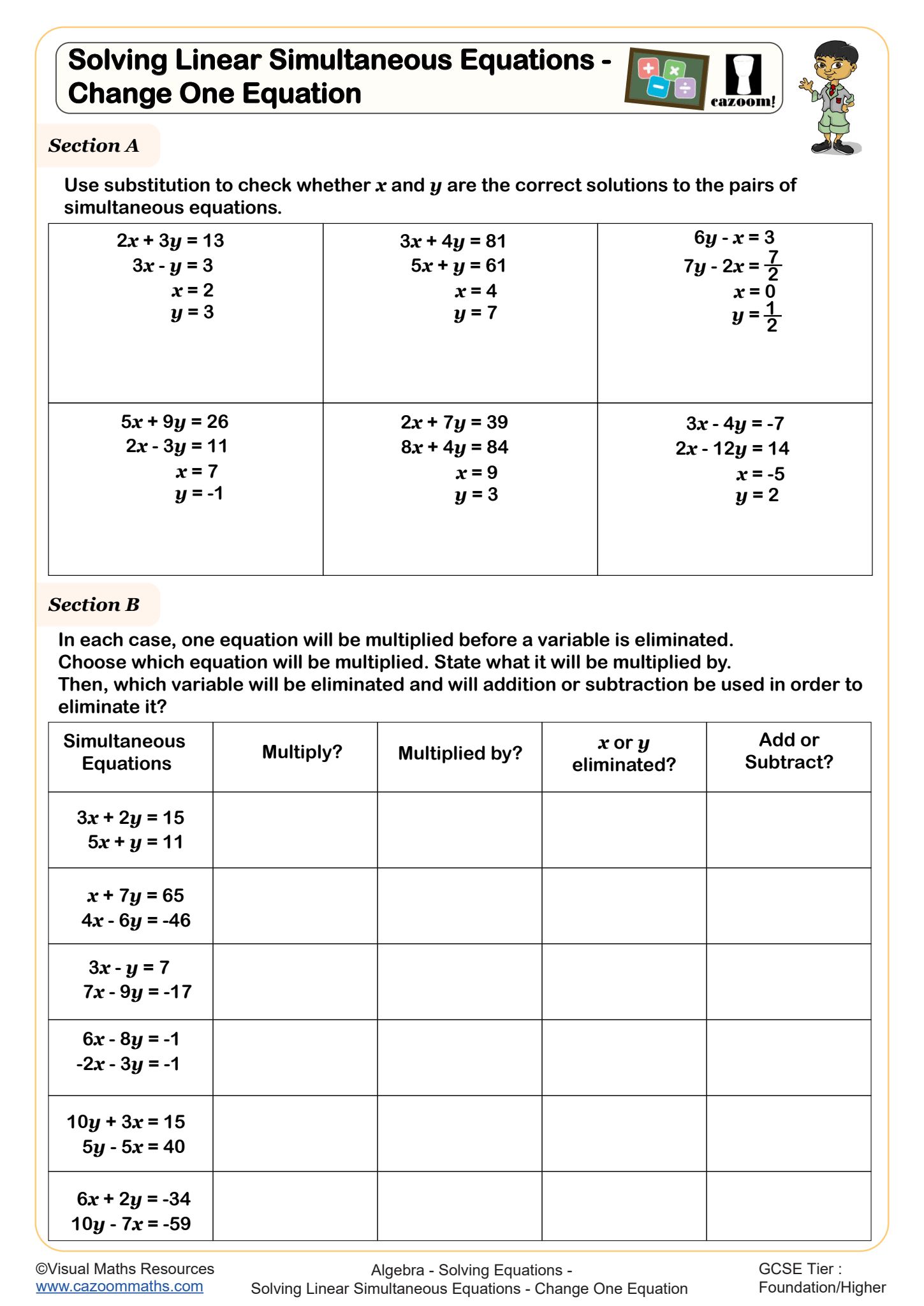
Solving Linear Simultaneous Equations - Change One Equation

Solving Linear Simultaneous Equations - Same Coefficients

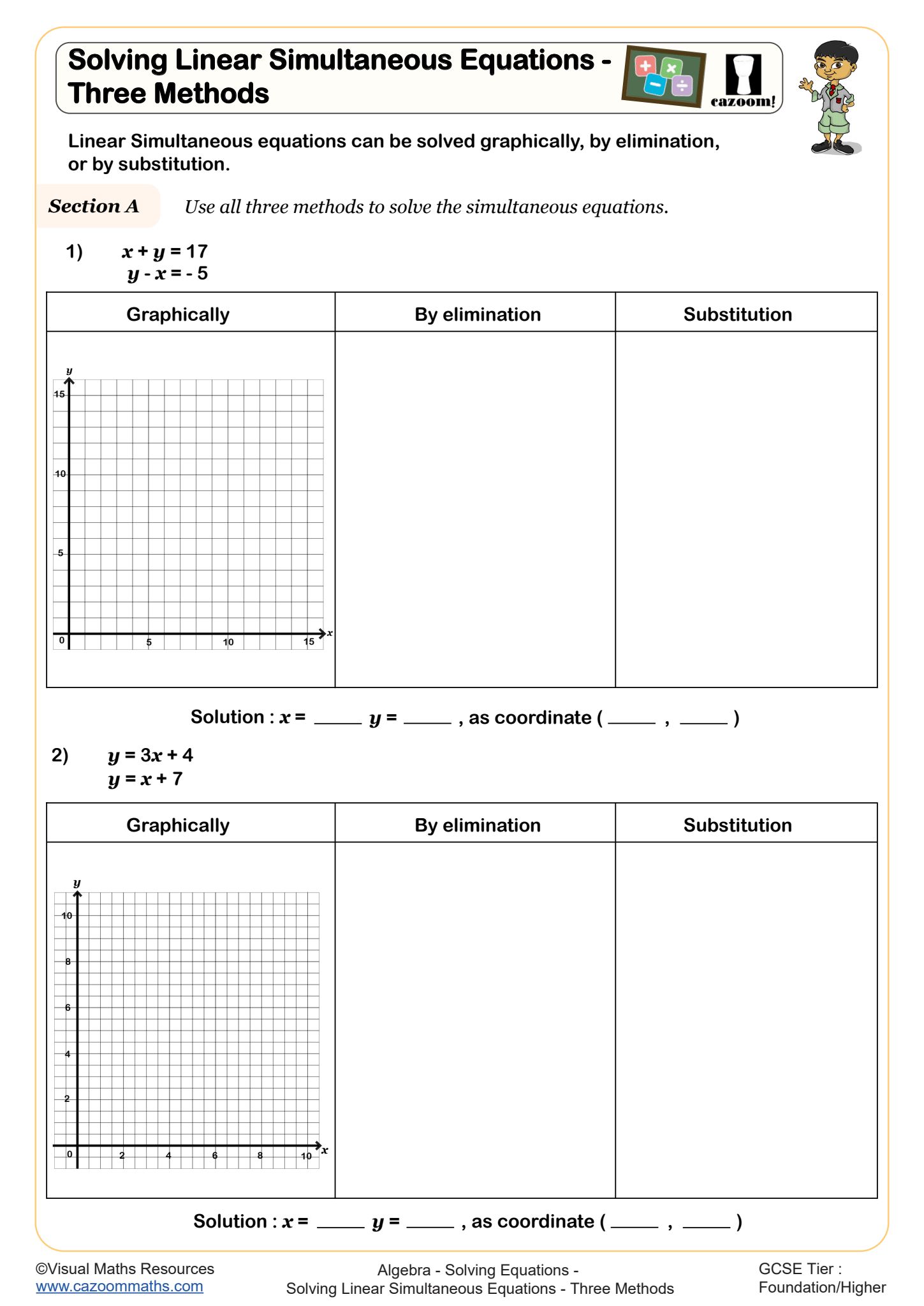
Solving Linear Simultaneous Equations - Three Methods

Solving Non-linear Simultaneous Equations

Solving One Step Equations with Algebra Tiles

Solving One Step Linear Equations

Solving Quadratic Equations (A)

Solving Quadratic Equations (B) (by Factorising)

Solving Quadratic Equations (C) (by Quadratic Formula)

Solving Quadratic Equations (D) (by Completing the Square)

Solving Quadratic Equations (E) - Using all Three Methods

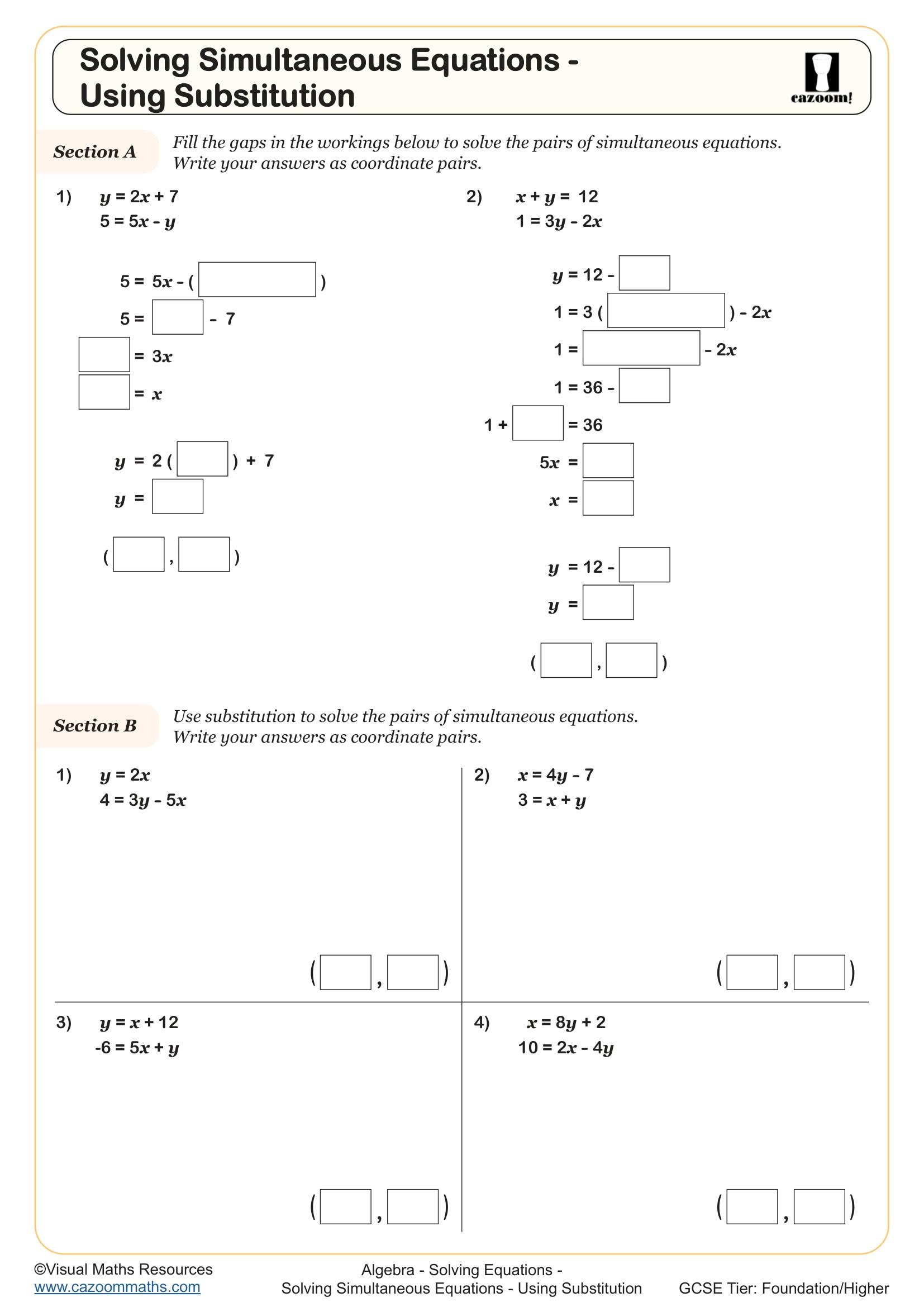
Solving Simultaneous Equations - Using Substitution

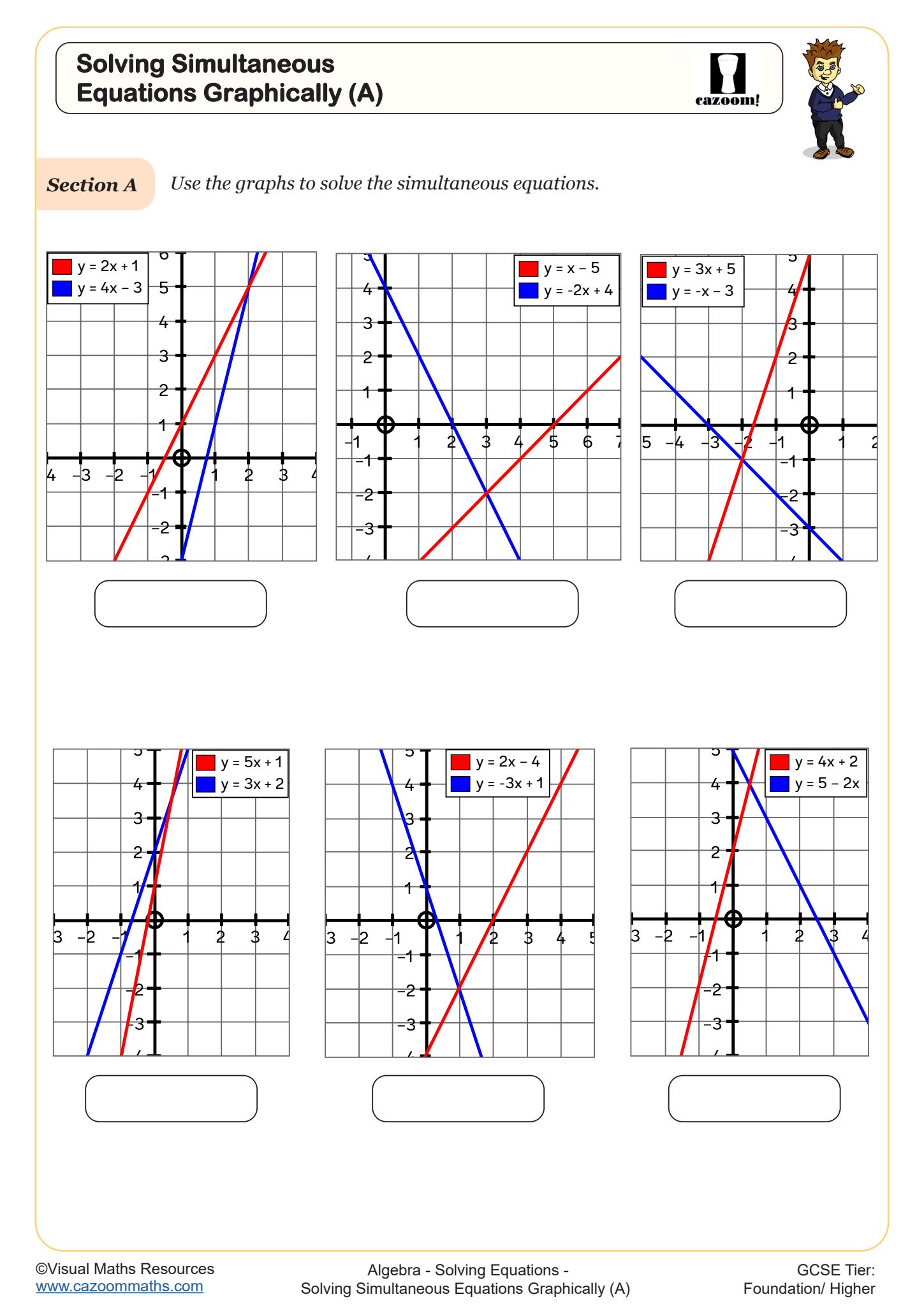
Solving Simultaneous Equations Graphically (A)

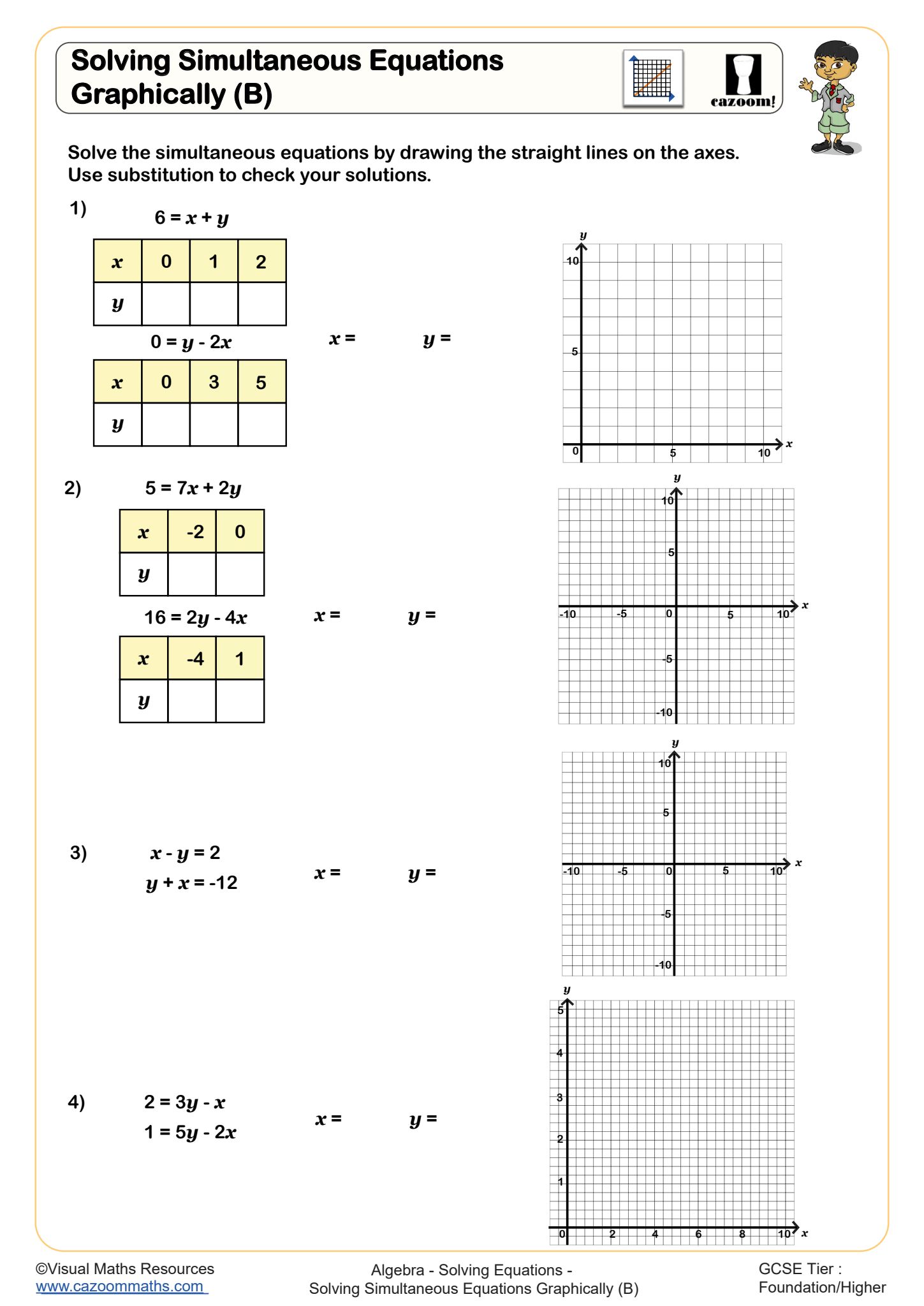
Solving Simultaneous Equations Graphically (B)

Solving Two Step Equations with Algebra Tiles

Trial and Improvement (A)

Trial and Improvement (B)

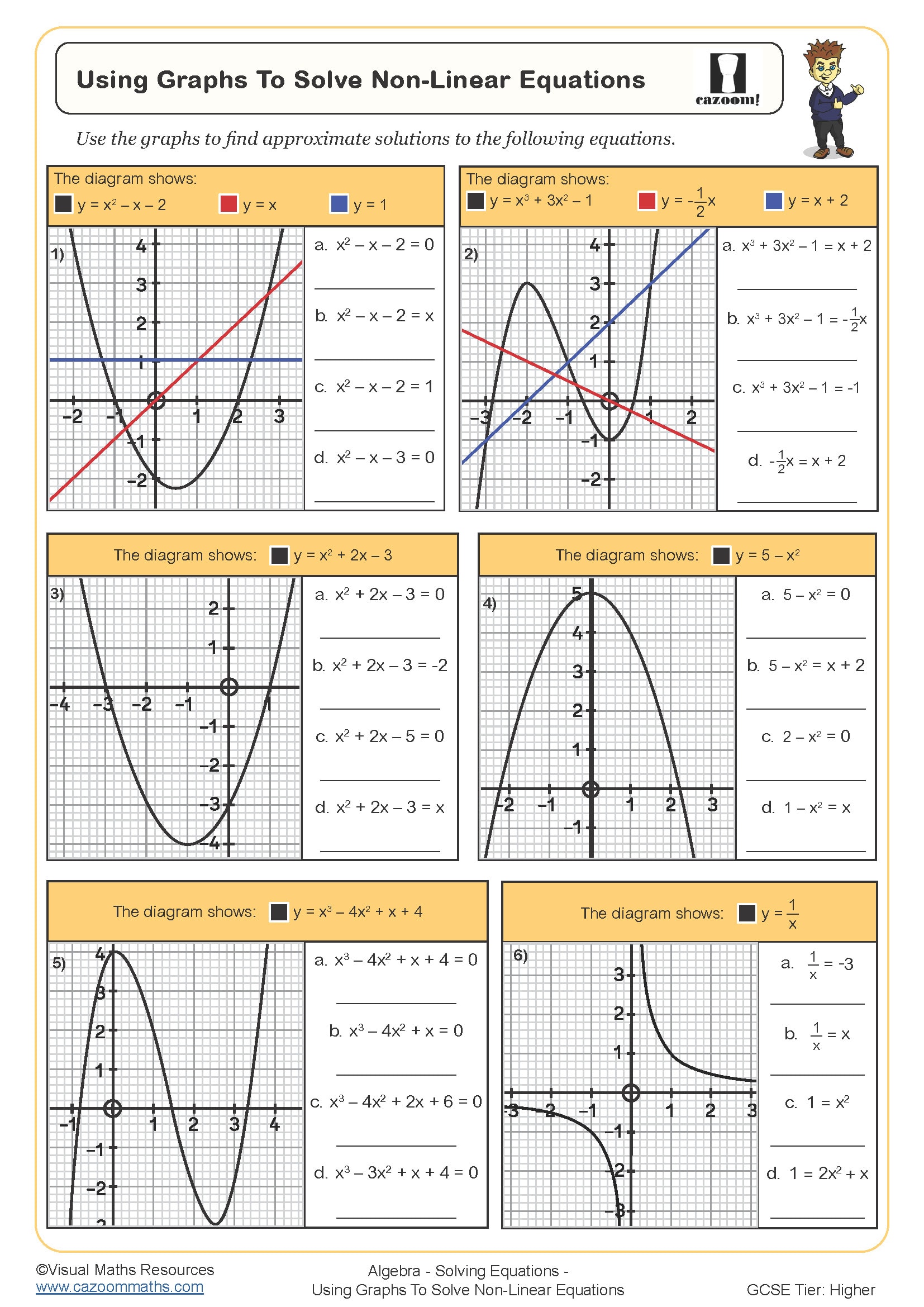
Using Graphs to Solve Non-linear Equations

How Our Printable Solving Equations Practice Transforms Year 10 Mathematical Understanding

Regular practice with varied equation types significantly accelerates student progress in Year 10 mathematics, particularly as learners encounter increasingly sophisticated algebraic manipulation requirements. The systematic approach embedded in these resources helps students recognise patterns across different equation structures, developing their ability to select appropriate solving strategies instinctively. This methodical progression ensures students build competence alongside speed, creating the automaticity needed for timed assessments where quick recall of solving methods proves essential. The deliberate sequencing from familiar techniques to advanced methods prevents cognitive overload whilst maintaining appropriate challenge levels. Through repeated exposure to different equation formats, students develop resilience when facing unfamiliar problems, learning to adapt known methods rather than memorising isolated procedures.

Specific learning benefits include:

• Masters multi-step algebraic manipulation techniques

• Develops systematic problem-solving approaches

• Strengthens mathematical reasoning and proof skills

• Prepares for GCSE exam question formats

• Builds fluency with quadratic methods

• Reinforces algebraic fraction manipulation

• Enhances accuracy in complex calculations

Topic Map: What Cazoom Maths Year 10 Solving Equation Resources Include

These worksheets progress from concrete numerical examples through pictorial representations to abstract algebraic forms, ensuring students grasp underlying concepts before advancing to symbolic manipulation. Each worksheet includes worked solutions that demonstrate step-by-step reasoning, allowing students to understand not just the answer but the mathematical thinking process behind each solution method.

The worksheets in this collection include:

• Solving Linear Equations — practising single and multi-step methods with increasing complexity

• Solving Equations with Unknowns on Both Sides — rearranging terms to isolate variables systematically

• Solving Quadratic Equations by Factorising — applying factorisation techniques to find quadratic roots

• Solving Quadratic Equations Using the Formula — using the quadratic formula for non-factorisable equations

• Completing the Square — transforming quadratics into vertex form for solving

• Solving Simultaneous Equations by Elimination — eliminating variables to find paired solutions efficiently

• Solving Simultaneous Equations by Substitution — substituting expressions to reduce equation systems methodically

• Solving Simultaneous Equations Graphically — finding intersection points through coordinate geometry approaches

Traditional Lessons or Worksheets? Why Year 10 Solving Equations Activities Work Best

The practical classroom focus of these resources addresses the diverse needs found in Year 10 mathematics classes, where students arrive with varying levels of algebraic knowledge. Each worksheet provides natural differentiation opportunities through tiered questions that challenge advanced learners whilst remaining accessible to those needing additional support. The inclusion of worked solutions showing complete mathematical reasoning saves valuable marking time whilst providing students with exemplar responses they can study independently. This balance between challenge and accessibility means teachers can use the same resource pack across mixed-ability groups, adapting delivery methods rather than sourcing multiple worksheet sets. The clear progression through equation types aligns perfectly with GCSE specification requirements, ensuring curriculum coverage remains comprehensive. Answer sheets enable rapid assessment, allowing teachers to identify misconceptions quickly and adjust instruction accordingly.

From Economy to Architecture: Where Equation-Solving Skills Apply Beyond the Classroom

Mathematical equation-solving underpins countless real-world calculations, from financial planning to scientific research. These fundamental skills enable precise problem-solving across professional and everyday contexts.

• Engineering design calculations for structural loads

• Financial modelling for loans and investments

• Scientific formula rearrangement in physics experiments

• Computer programming logic and algorithm development

• Economic forecasting and business analysis

• Medical dosage calculations based on patient variables

• Sports performance analysis and statistical predictions

• Architecture and construction project planning