Year 8 Function Machines Worksheets
How Teachers Use Year 8 Function Machine Worksheets to Save Planning Time
The function machines transform abstract algebra into visual and manageable steps which Year 8 students can learn progressively. Students who visualise mathematical relationships through input-output diagrams find it easier to transition from basic algebraic notation to complex operations in Year 7. The structured practice of these resources enables students to recognise patterns and predict outcomes while developing essential reasoning skills needed for future mathematical education. The visual approach provides specific support to students who find traditional algebra difficult because it provides different ways to understand mathematical concepts. Students who practice function machine problems consistently develop stronger mathematical fluency while finding algebra more accessible.
Specific learning benefits include:
• Connects number patterns to algebraic expressions
• Develops reverse operation thinking
• Strengthens equation-solving foundations
• Improves mathematical reasoning skills
• Introduces formal mathematical notation
• Creates systematic problem-solving approaches
• Supports visual learning preferences
Classroom-Ready Worksheet Topics for Lessons, Homework, and Revision
These worksheets progress systematically through increasing complexity levels, ensuring students grasp each concept before advancing. Visual diagrams accompany each problem, making abstract relationships concrete and accessible for diverse learners. Resources include both forward operations (finding outputs) and inverse problems (finding inputs or operations), developing a comprehensive understanding. The materials bridge the gap between arithmetic operations and formal algebraic manipulation through graduated exercises.
The core skills covered include:
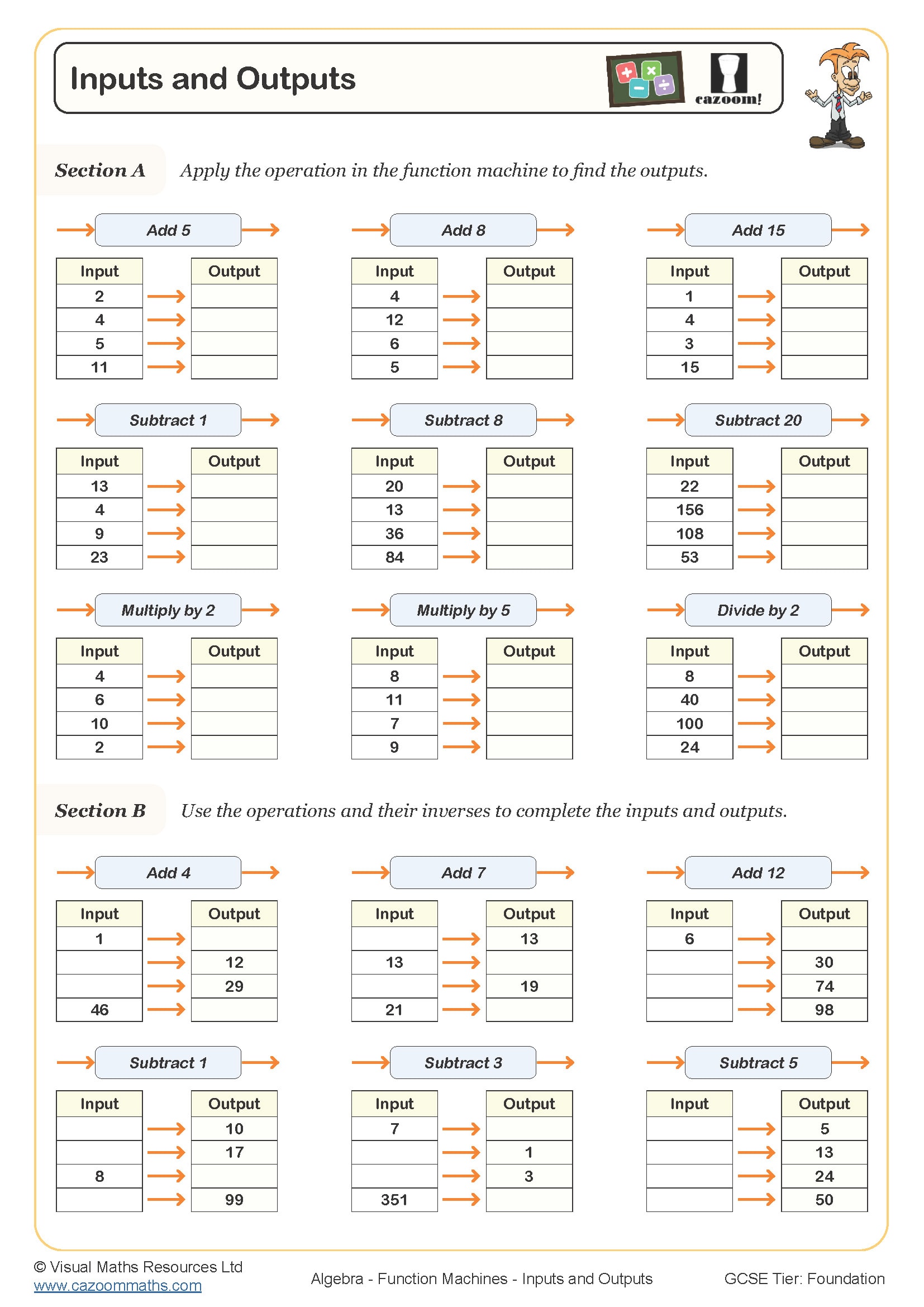
• Single-operation machines – addition, subtraction, multiplication, division basics
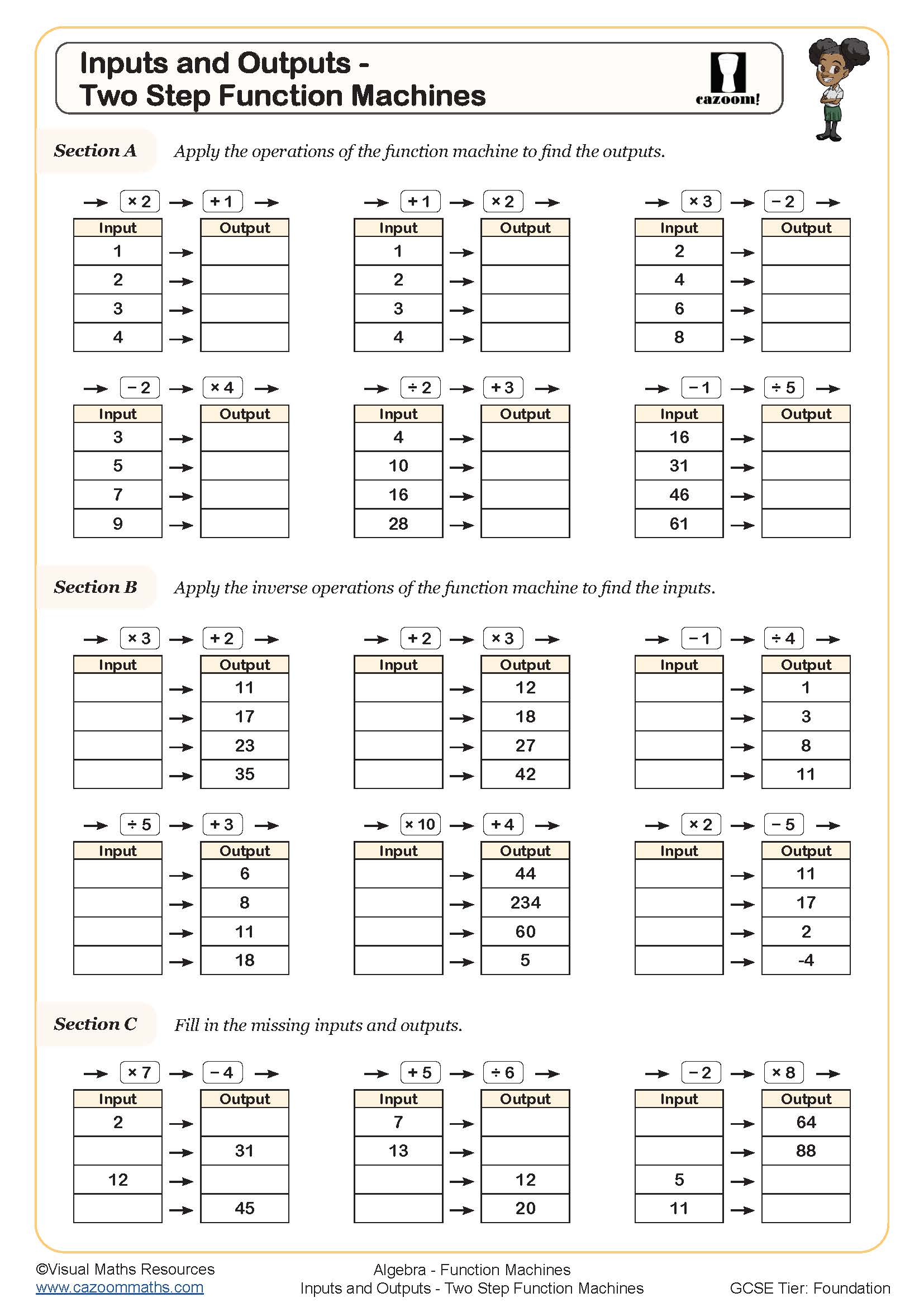
• Two-step function machines – combining operations in sequence
• Inverse operations – working backwards to find inputs
• Finding the function – determining operations from given inputs/outputs
• Multi-step functions – complex chains of operations
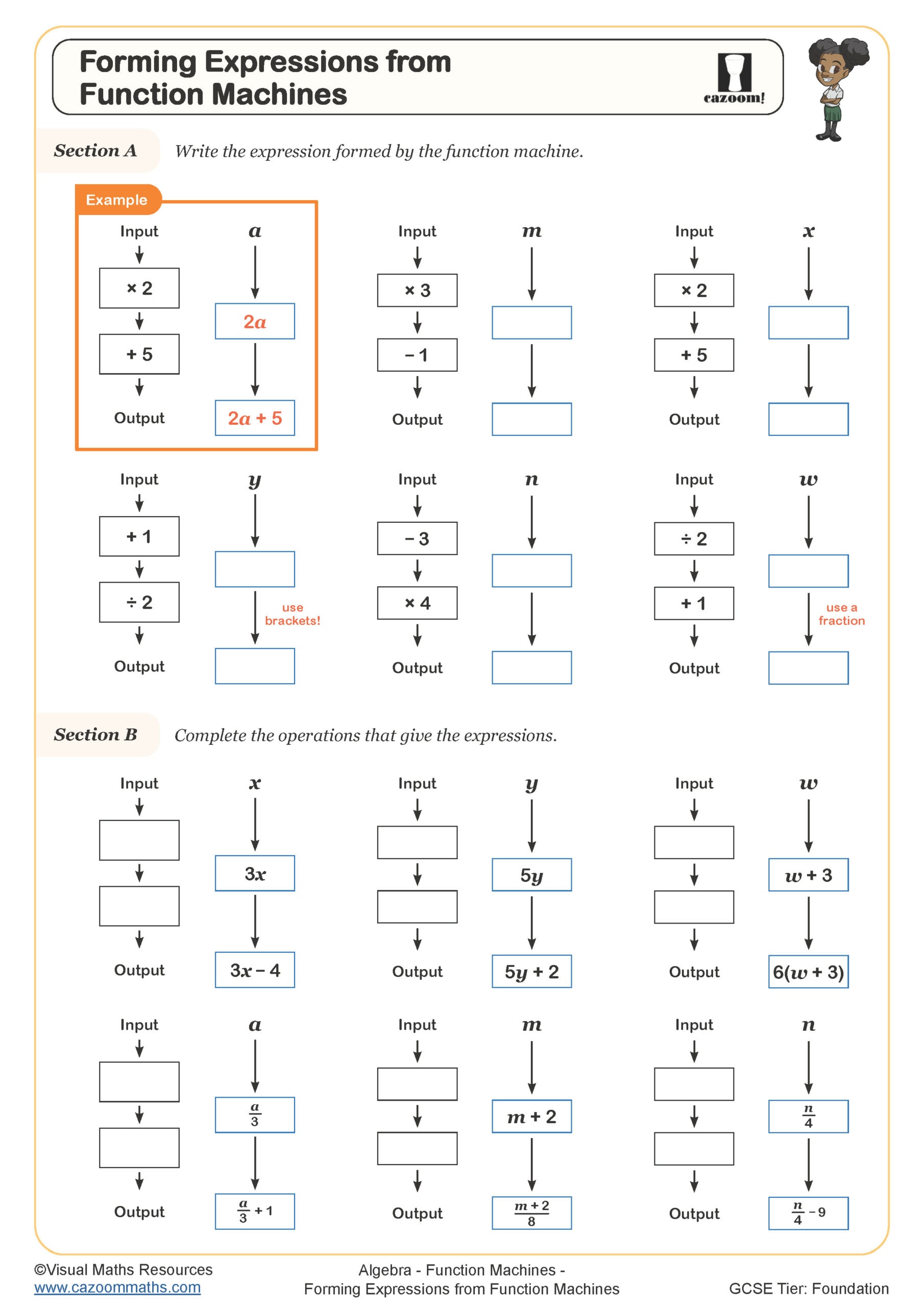
• Algebraic notation – writing functions using algebra
• Substitution skills – replacing variables with values
• Linear sequences – connecting to number patterns
• Problem-solving strategies – systematic approaches to unknowns
Support Your Child’s Learning With KS3 Function Machine Worksheets
Secondary maths departments value these worksheets for their careful differentiation and classroom-ready format. The resources contain multiple entry points, which enable teachers to support struggling students and extend confident learners at the same time during a lesson. The combination of visual aids with algebraic symbols supports students with varying levels of mathematical understanding. The answer sheets with worked solutions reduce grading time while giving students precise examples to evaluate their work. The progression follows the teaching sequences which research in maths education recommends. Teachers state that function machines specifically assist students who were unable to understand algebra before, thus making these resources essential for teaching students of different abilities. The structured format allows students to learn independently, so teachers can offer individualised support to students who need it most.
Everyday Maths: Where Year 8 Students Use Function Machine Skills in Real Life
Understanding function machines equips Year 8 students with logical thinking skills applicable across numerous real-world scenarios. These mathematical relationships appear in everyday situations where inputs transform into outputs through consistent processes.
• Computer programming – understanding how code processes inputs
• Recipe scaling – adjusting quantities whilst maintaining proportions
• Currency conversion – applying exchange rates systematically
• Mobile phone tariffs – calculating costs from usage patterns
• Sports scoring systems – converting performances into points
• Manufacturing processes – predicting outputs from raw materials
• Scientific formulas – relating variables in experiments
• Budget planning – projecting expenses from spending patterns