Year 8 Sequences Worksheets
Continuing Sequences from Patterns
Finding Arithmetic nth Terms Worksheet
Finding nth Terms from Patterns
Finding Quadratic Sequence nth Terms
Generating Sequences from the Nth Term
Generating Sequences from the Term to Term Rule
Geometric Sequences (A)
Geometric Sequences (B)
Quadratic Sequences
Quadratic Sequences - Using the Quadratic Sequence Formula
Special Sequences
Using the Nth Term (Linear)
How Year 8 Sequences Practice Builds Secure, Transferable Algebra Skills
Well-sequenced tasks help pupils notice structure, state a rule, and then generalise it. By revisiting the same idea through different representations, learners reduce common slips—such as mixing up position and value—and gain the precision needed for reliable algebra. Short checks and reasoning prompts encourage pupils to justify steps rather than rely on pattern-spotting alone. This consistent approach supports steady progress across the term and readiness for in-class assessments. Specific learning benefits include:
• Identifies constant first differences in linear patterns
• Links diagrams, tables, and algebraic expressions fluently
• Forms and uses nth-term rules with clarity
• Tests sequence membership and locates given terms
• Explains reasoning in concise mathematical language
• Builds independent practice routines at home or in class
What Year 8 Sequences Worksheets Cover: Rules, nth Term, and Much More
Pupils move from concrete and pictorial growth patterns to symbolic rules, then apply those rules to generate terms and justify membership. Worked answers are included to model efficient methods and tidy notation without overexplaining—useful for self-marking and quick feedback.
The worksheets in this collection include:
• Finding Arithmetic nth Terms Worksheet — Use first differences to form a linear general term.
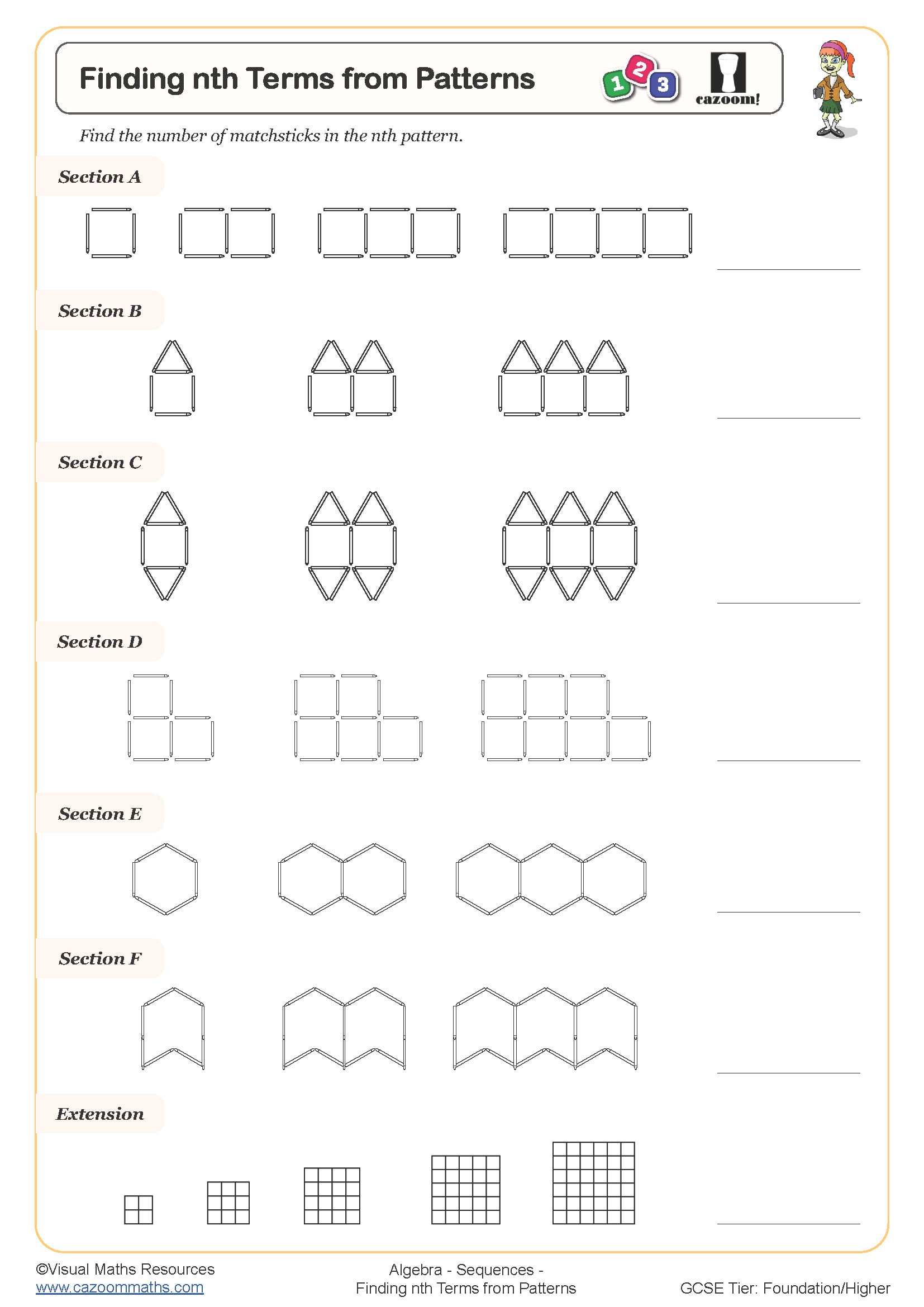
• Finding nth Terms from Patterns — Generalise visual growth into concise algebraic expressions.
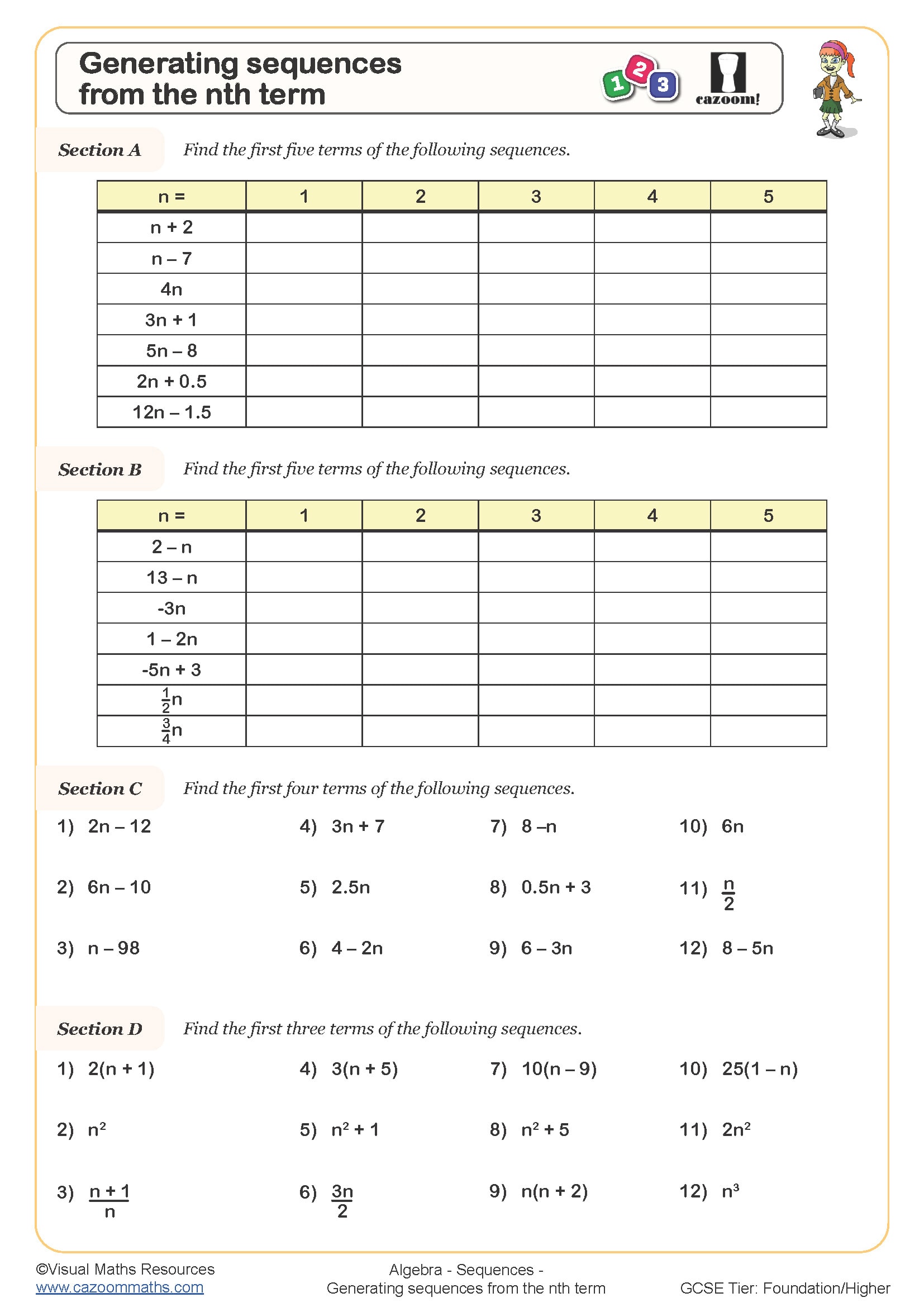
• Generating Sequences from the Nth Term — Substitute positions to produce values efficiently.
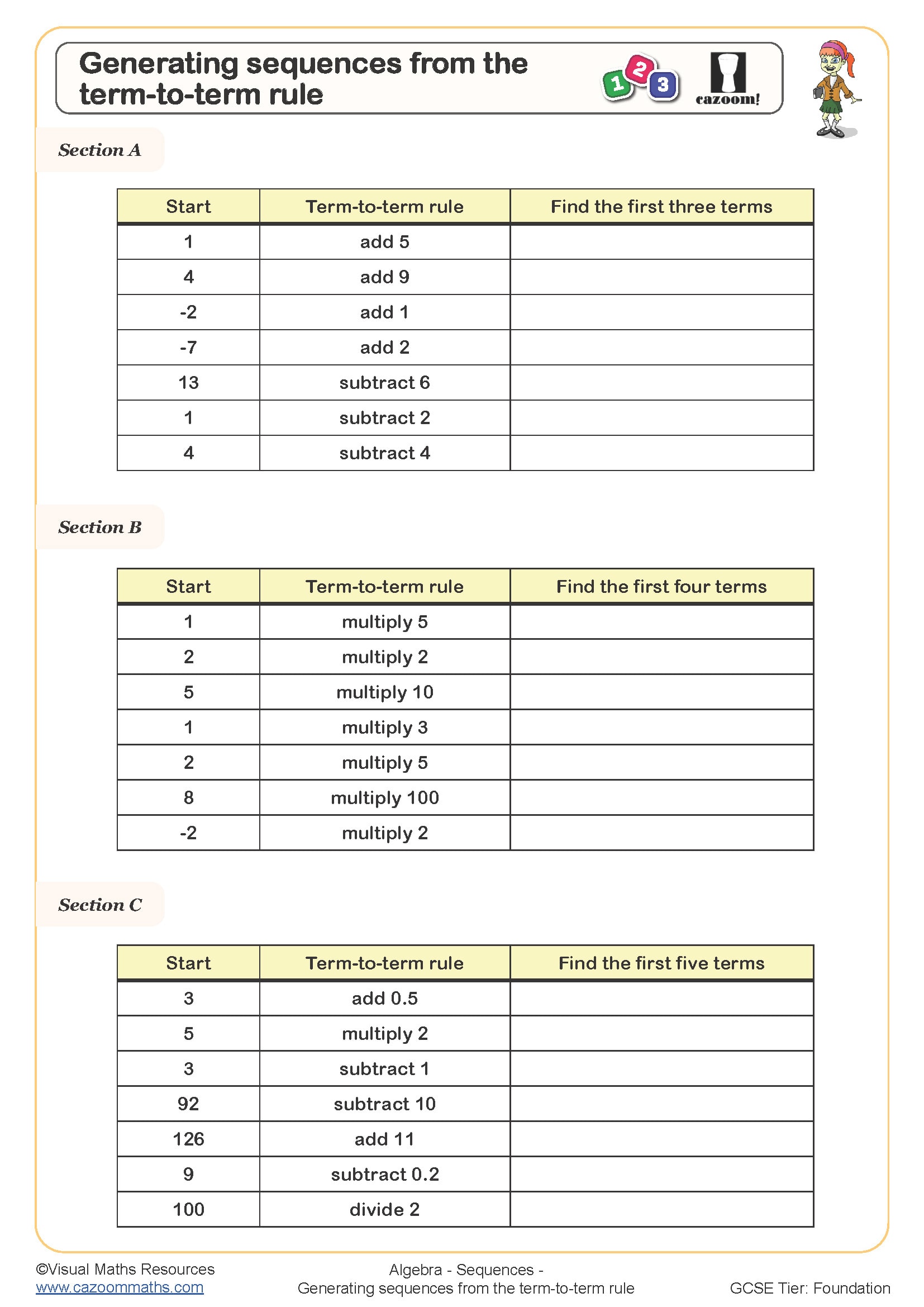
• Generating Sequences from the Term-to-Term Rule — Apply recursive steps and connect to tabular representations.
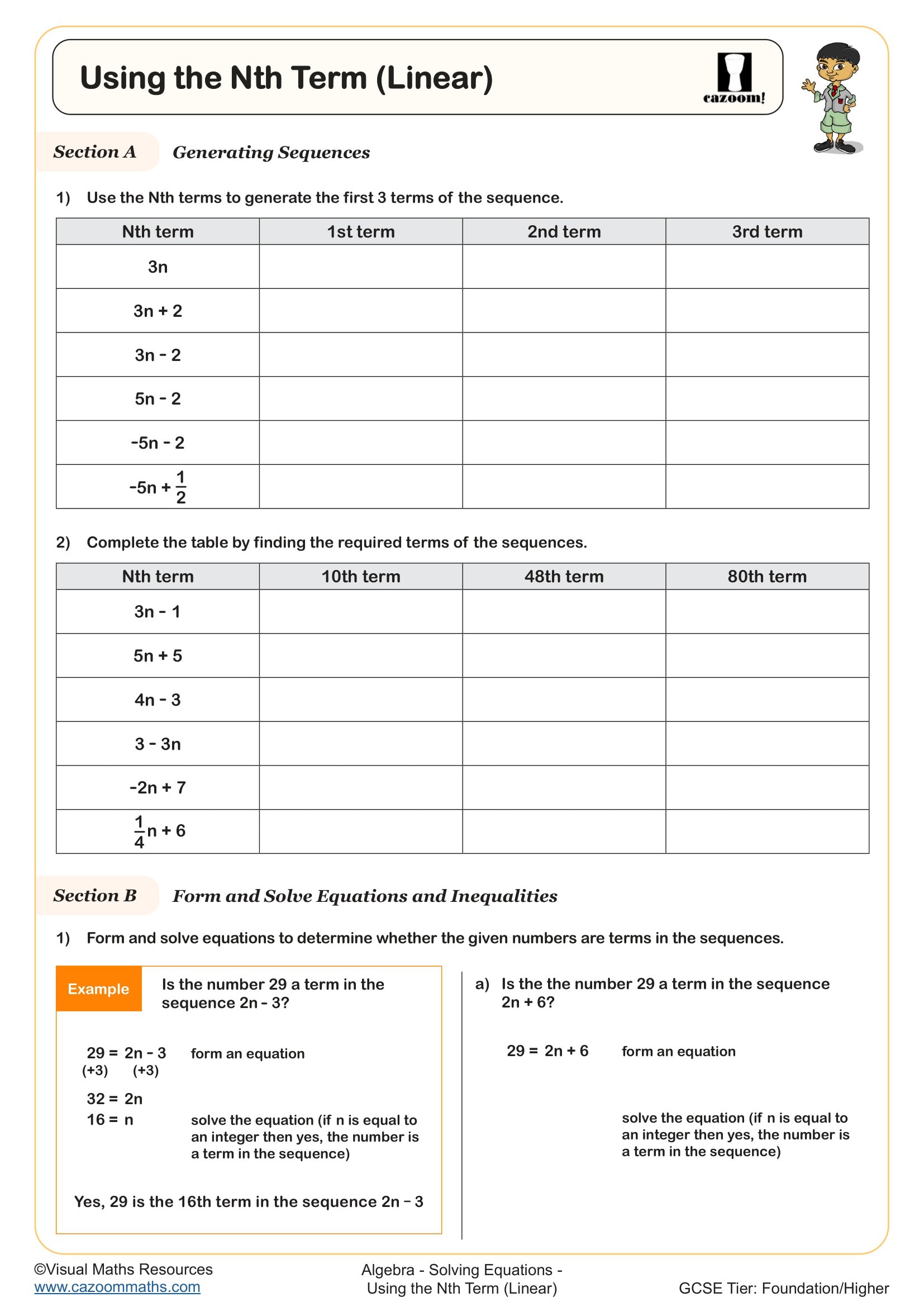
• Using the Nth Term (Linear) — Decide membership, find positions, and justify reasoning.
Why Teachers Choose Our Year 8 Sequences Worksheets for KS3
Class-ready layouts make it easy to start, model, and check within a single lesson. Initially, the primary questions offer accessible practice; later items require explaining methods, verifying results, and correcting misconceptions—ideal for mixed-attainment groups without creating separate worksheets. Differentiation stems from the depth of reasoning rather than changing the task entirely, allowing everyone to work on the same learning goal. Full solutions display both the method and the outcome, saving planning time and enabling pupils to self-assess accurately. Whether used for a focused starter, a main practice set, or homework, the structure stays consistent so routines stick. The result is fewer avoidable errors, cleaner algebra, and greater confidence with generalisation—skills that support broader KS3 algebra strands.
Where Sequence Reasoning Appears in Everyday Life for Year 8
Linear growth and position-to-value reasoning crop up in many familiar settings, helping pupils make predictions and explain them clearly.
• Forecasting savings with a fixed weekly or monthly deposit
• Reading timetables built around constant time intervals
• Planning training that increases by the same amount each session
• Estimating materials for repeating tiling or design patterns
• Tracking loyalty points or reward schemes that grow steadily
• Writing simple code loops that update a variable by a constant step
• Modelling steady temperature changes in basic science experiments