Year 9 Sequences Worksheets
Continuing Sequences from Patterns
Finding Arithmetic nth Terms Worksheet
Finding nth Terms from Patterns
Finding Quadratic Sequence nth Terms
Generating Sequences from the Nth Term
Generating Sequences from the Term to Term Rule
Geometric Sequences (A)
Geometric Sequences (B)
Quadratic Sequences
Quadratic Sequences - Using the Quadratic Sequence Formula
Special Sequences
Using the Nth Term (Linear)
How Year 9 Sequences Practice Builds Secure, Transferable Algebra Skills
Tasks that are in a logical sequence assist learners in identifying patterns, generating a rule, and then generalising to new situations. Students are able to see that position and value are important components of algebra and that they can be distinguished in other situations, thereby evading a variety of misconceptions. Short checks and reasoning prompts are a means of assisting learners in analysing and articulating their process instead of passive pattern recognition. This approach fosters developmental learning, which in turn improves test performance.
Some specific learning benefits are:
• Identifies consistent initial variations in linear patterns
• Connects algebraic expressions, tables, and diagrams with ease.
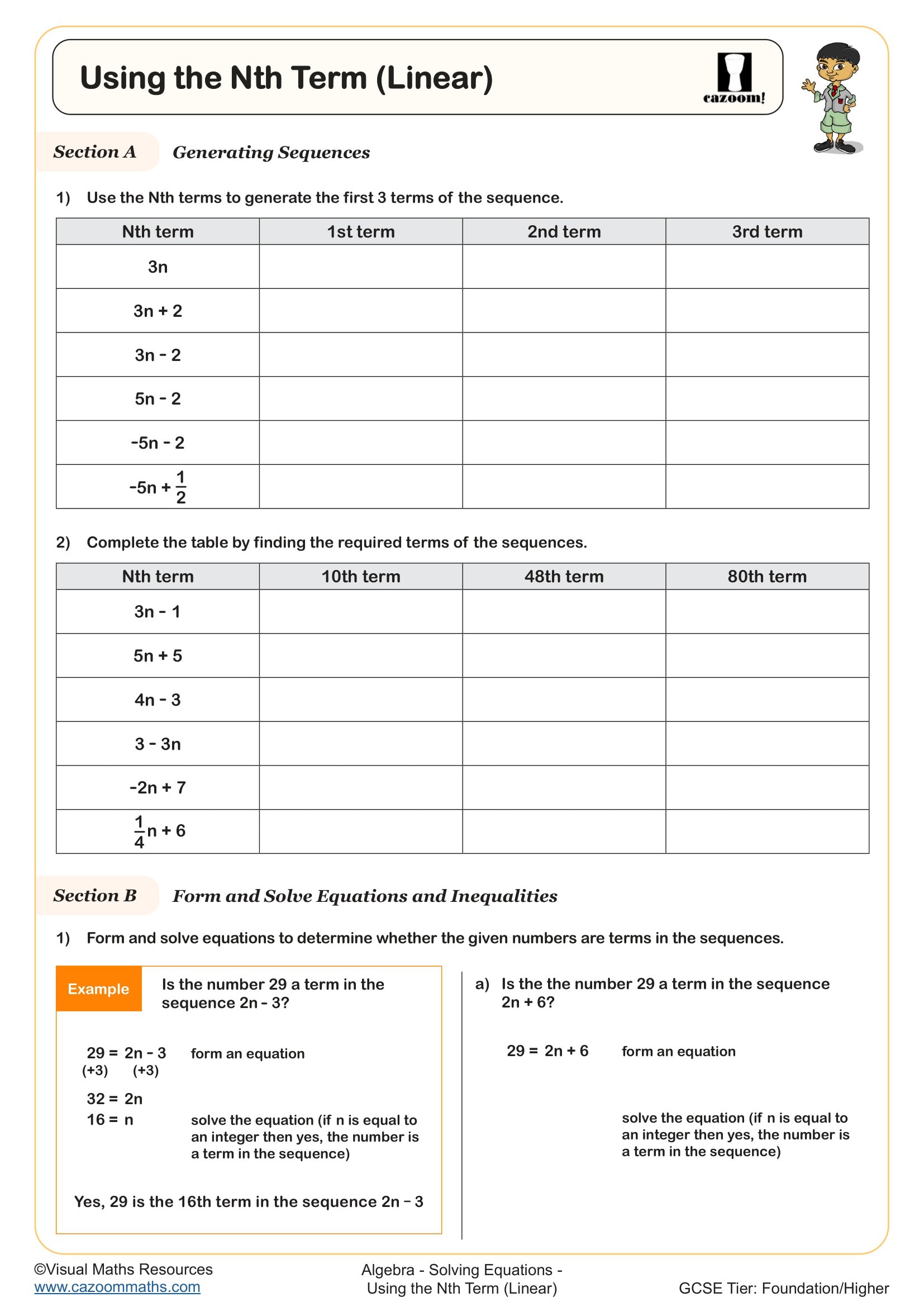
• Form and apply nth-term rules properly
• To determine whether a term is part of a sequence.
• Explains logic in simple, understandable mathematical terms.
• Establishes independent practice routines for them to follow at home or in class.
What Year 9 Sequences Worksheets Cover: Rules, nth Term, and Much More
Pupils move from concrete and pictorial growth patterns to symbolic rules, then apply those rules to generate terms and justify membership. Worked answers are included to model efficient methods and tidy notation without overexplaining—useful for self-marking and quick feedback.
The worksheets in this collection include:
• Linear Sequences — finding patterns in arithmetic progressions with constant differences
• Nth Term of Linear Sequences — deriving algebraic formulas from number patterns
• Geometric Sequences — exploring multiplicative patterns and common ratios
• Quadratic Sequences — analysing second differences to identify polynomial patterns
• Special Number Sequences — investigating Fibonacci, triangular and square numbers
• Finding Missing Terms — applying sequence rules to complete number patterns
• Sequences from Patterns — connecting visual arrangements to numerical progressions
Why Teachers Choose Our Year 9 Sequences Worksheets for KS3
With class-ready layouts, you can easily start, model, and check all in one lesson. Initially, the primary questions are low-hanging fruit; subsequent questions involve method explanation, result validation, and misconception aliasing. This is beneficial to heterogeneous groups, as they can avoid the need for individualised worksheets. Differentiation is not in the complete abandonment of the task, but in the depth of thought that is given to the problem. This is beneficial, as the learning objectives remain intact. Complete solutions avoid the nuanced planning of just the outcomes and allow for self-assessment. This is beneficial for focus, as the start, main, and homework shifts are seamless to participants. The result is avoided errors, clearer algebra, and most importantly, heightened confidence.
Where Sequence Reasoning Appears in Everyday Life for Year 9
Many events in daily life allow for estimation and reasoning by linear growth and position-to-value reasoning, which assists learners in making more accurate, clear explanations. For Example-
• Predicting savings based on weekly or monthly fixed deposits
• Interpreting Routines on the Basis of Time Intervals
• Training on the Basis of Increasing Difficulty Each Iteration
• Estimating the Materials in the Repetition of Tiling or Design Patterns
• Tracking Loyalty Points or Reward Systems which Gradually Increase
• Creating Simple Code Loops where a Designated Variable Increases by a Constant Value
• Simulating Constant Ambient Temperature Changes in Simple Scientific Experiments