Reflection Worksheets
All worksheets are created by the team of experienced teachers at Cazoom Maths.
What Are Reflection Math Worksheets and How Do They Help Students?
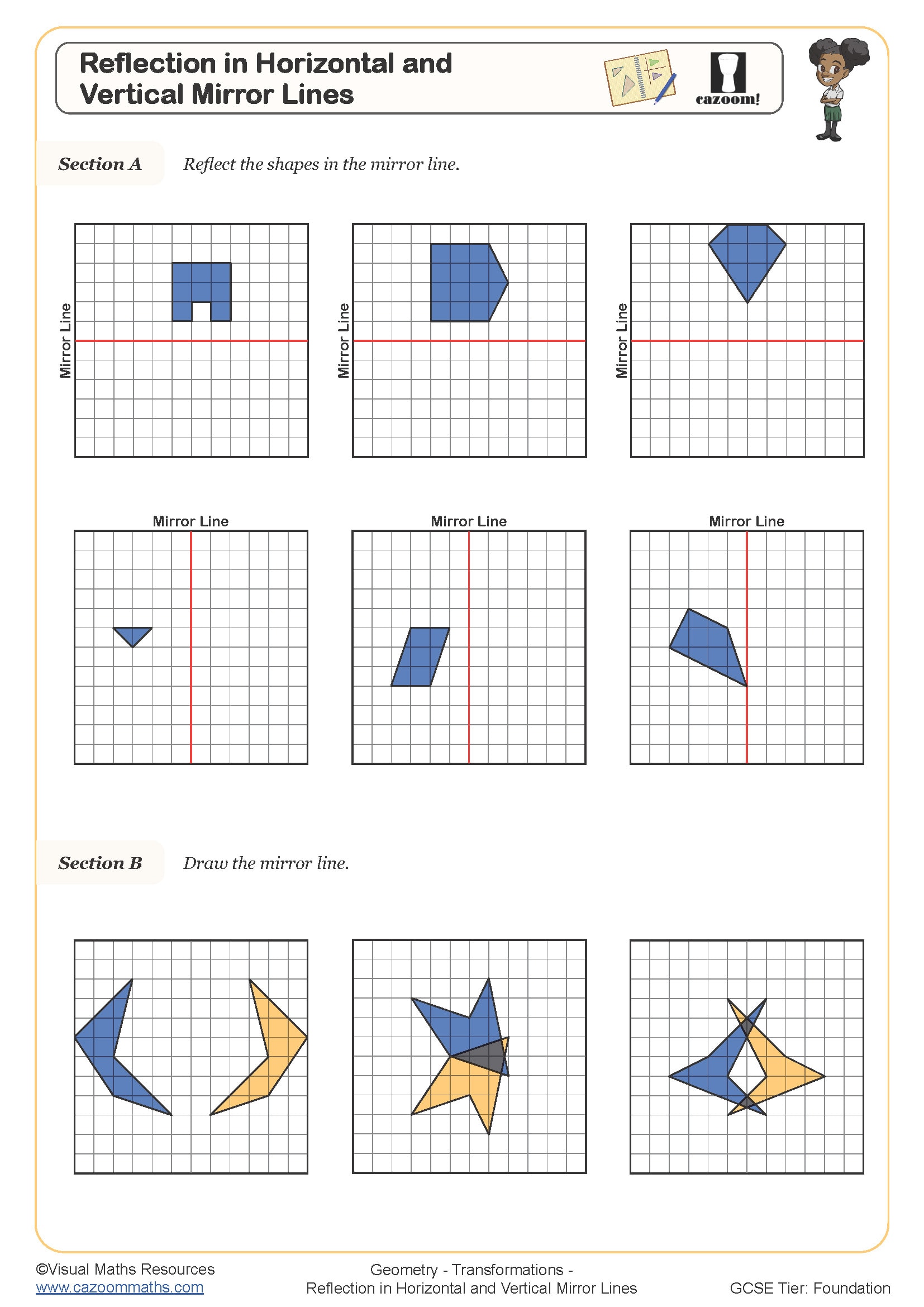
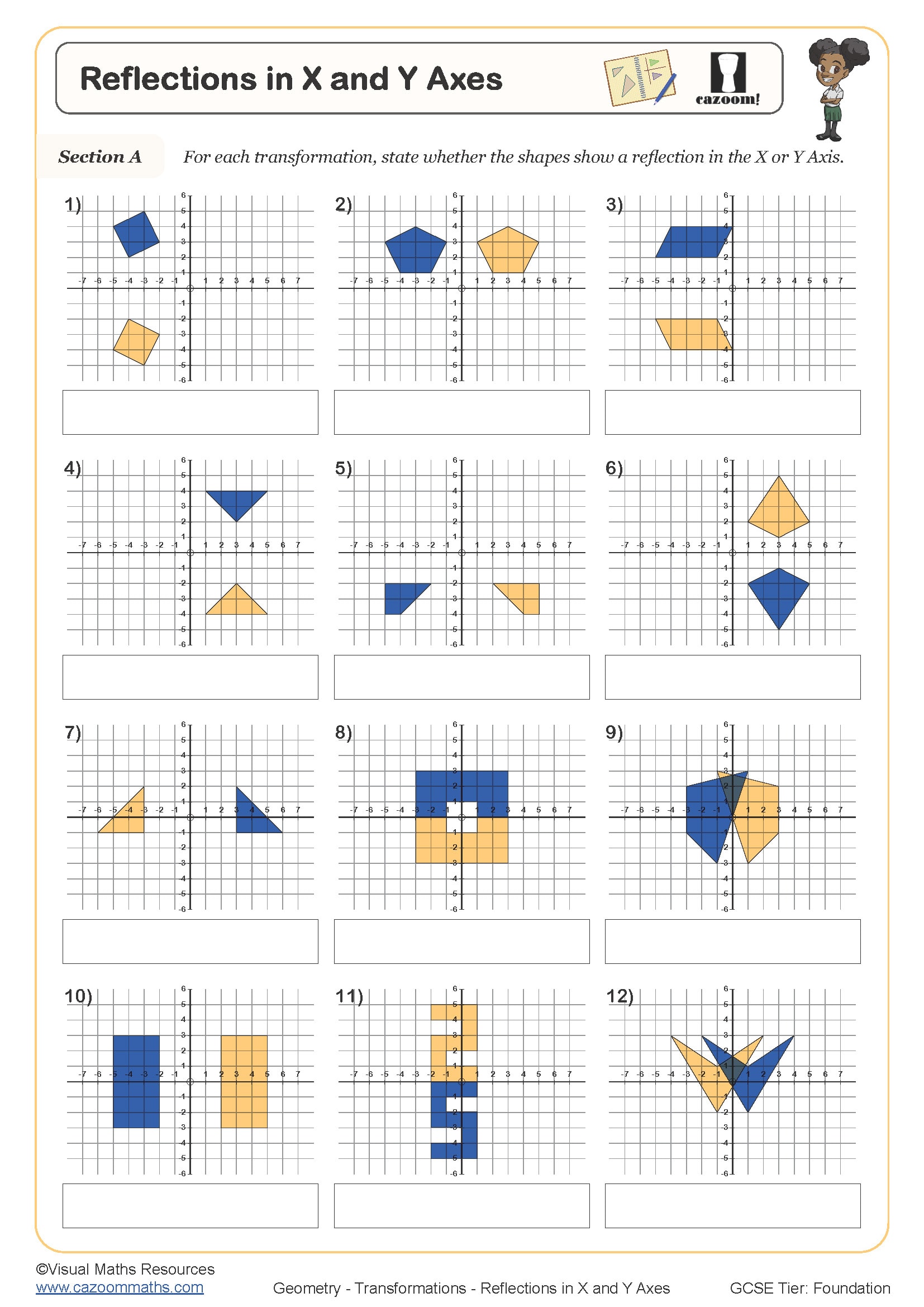
Reflection math worksheets provide structured practice in transforming shapes across mirror lines on coordinate grids. At KS3, students work with reflections in the x-axis, y-axis, and lines such as y = x or y = -x, progressing from simple polygons to more complex shapes that require careful plotting of multiple coordinates. These exercises build the foundation for the transformations content that appears in GCSE examinations, where students must identify, describe, and perform reflections accurately.
A common misconception involves students simply flipping shapes without maintaining equal perpendicular distance from the mirror line. Teachers often see coordinates reflected incorrectly when the mirror line is diagonal, with students counting horizontally and vertically rather than measuring at right angles to the line itself. The worksheets address this through varied question types that require students to check their transformed coordinates systematically, helping them recognise when reflections preserve shape and size whilst changing orientation.
Which Year Groups Study Reflections?
Reflection appears in the KS3 curriculum across Years 7, 8, and 9, forming part of the transformations strand within geometry. Students first encounter basic reflections in vertical and horizontal mirror lines during Year 7, building on informal work with symmetry from primary school. The topic connects directly to National Curriculum requirements for understanding and performing geometric transformations on coordinate grids.
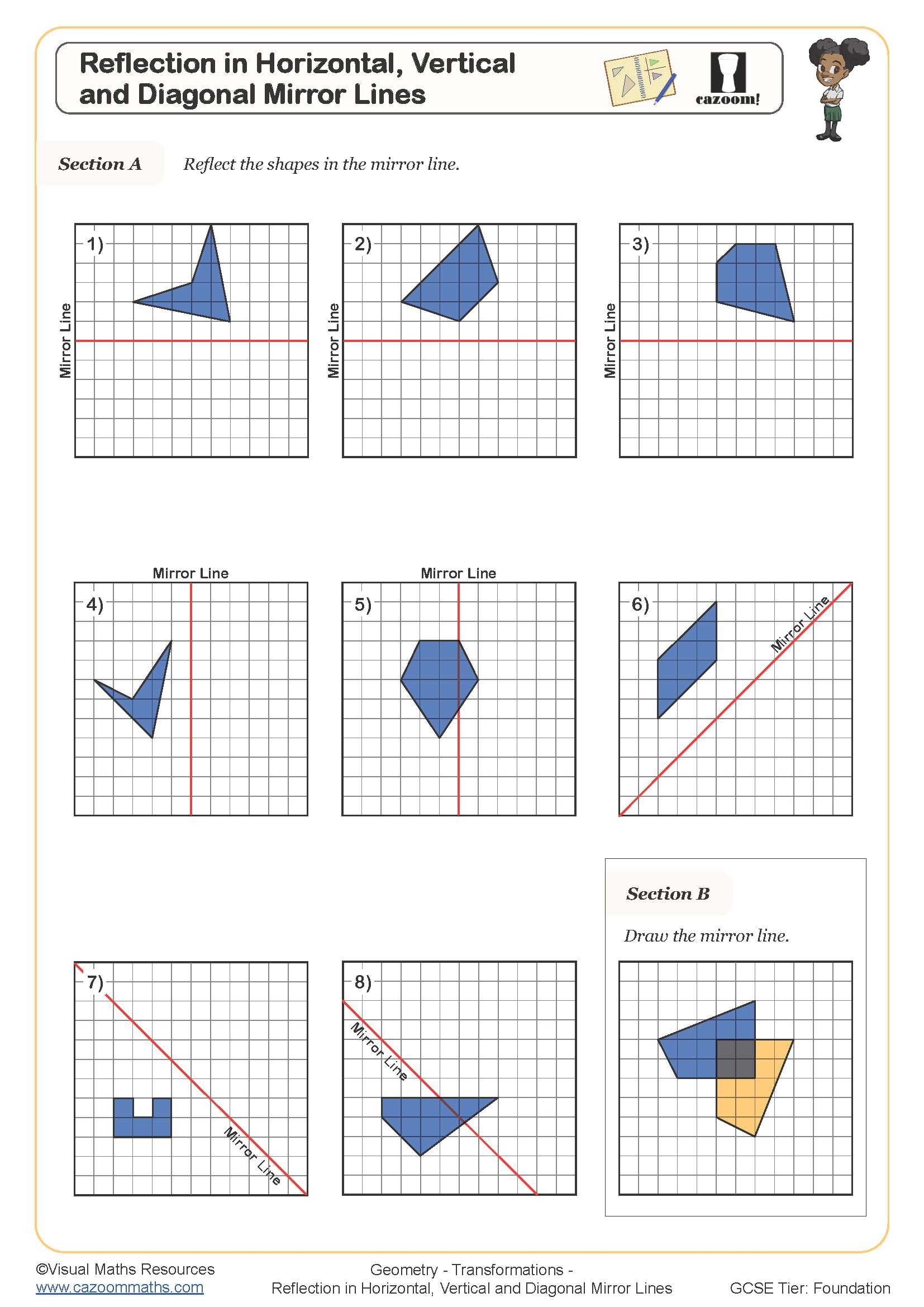
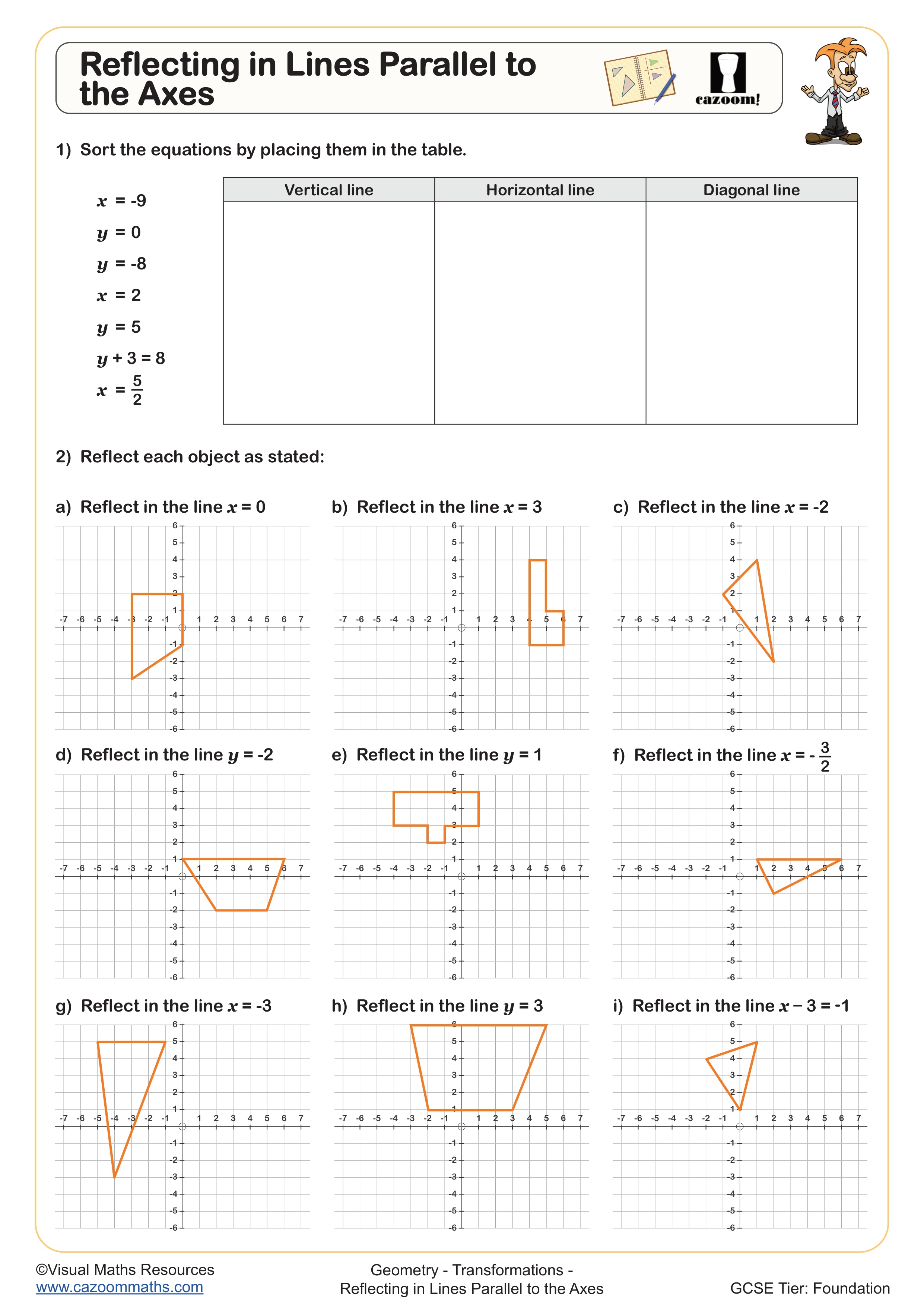
Progression across these year groups involves increasing complexity of mirror lines and shapes. Year 7 typically focuses on reflections in the axes and simple vertical or horizontal lines like x = 2. By Year 8, students tackle diagonal mirror lines such as y = x, which require more sophisticated coordinate manipulation. Year 9 work often combines reflections with other transformations and expects students to describe reflections using precise mathematical language, including identifying the equation of the mirror line from a given transformation.
How Do Students Reflect Shapes in Diagonal Mirror Lines?
Reflecting shapes in diagonal mirror lines requires students to understand that each point and its image must be equidistant from the line, measured perpendicular to it. For y = x, a useful pattern emerges: coordinates swap positions, so (3, 1) becomes (1, 3). For y = -x, coordinates swap and change sign. However, teachers notice that many students try to apply these shortcuts without understanding the underlying geometry, leading to errors when the mirror line is offset, such as y = x + 2.
This skill connects to real-world applications in design and engineering, particularly in computer graphics and animation. Programmers use reflection algorithms to create symmetrical patterns, mirror effects in games, and realistic lighting effects where surfaces reflect objects. Architects apply reflection principles when designing buildings with glass facades that mirror surrounding structures. Understanding how coordinates transform under reflection helps students grasp how digital images are manipulated in software, a fundamental concept in modern STEM fields where geometric transformations underpin everything from medical imaging to satellite navigation systems.
How Can Teachers Use These Reflection Worksheets in the Classroom?
The worksheets provide scaffolded practice that allows students to build confidence with increasingly challenging reflection tasks. Starting with reflections in axes before progressing to diagonal mirror lines, the questions help students develop systematic approaches to checking their work, such as verifying that distances from the mirror line match. The included answer sheets support self-assessment and peer marking, enabling students to identify errors in their method rather than just checking final answers.
Many teachers use these resources during intervention sessions with students who find transformations difficult, as the structured progression allows targeted practice on specific mirror lines. They work well as homework following initial teaching, giving students time to apply methods carefully without time pressure. In paired work, one student can perform the reflection whilst their partner checks measurements, encouraging mathematical discussion about perpendicular distance and coordinate relationships. The worksheets also serve as quick revision tools before assessments, helping students refresh their understanding of notation and technique that exam mark schemes specifically reward.