Similarity Worksheets
Similar Shapes
Year groups: 8, 9, 10
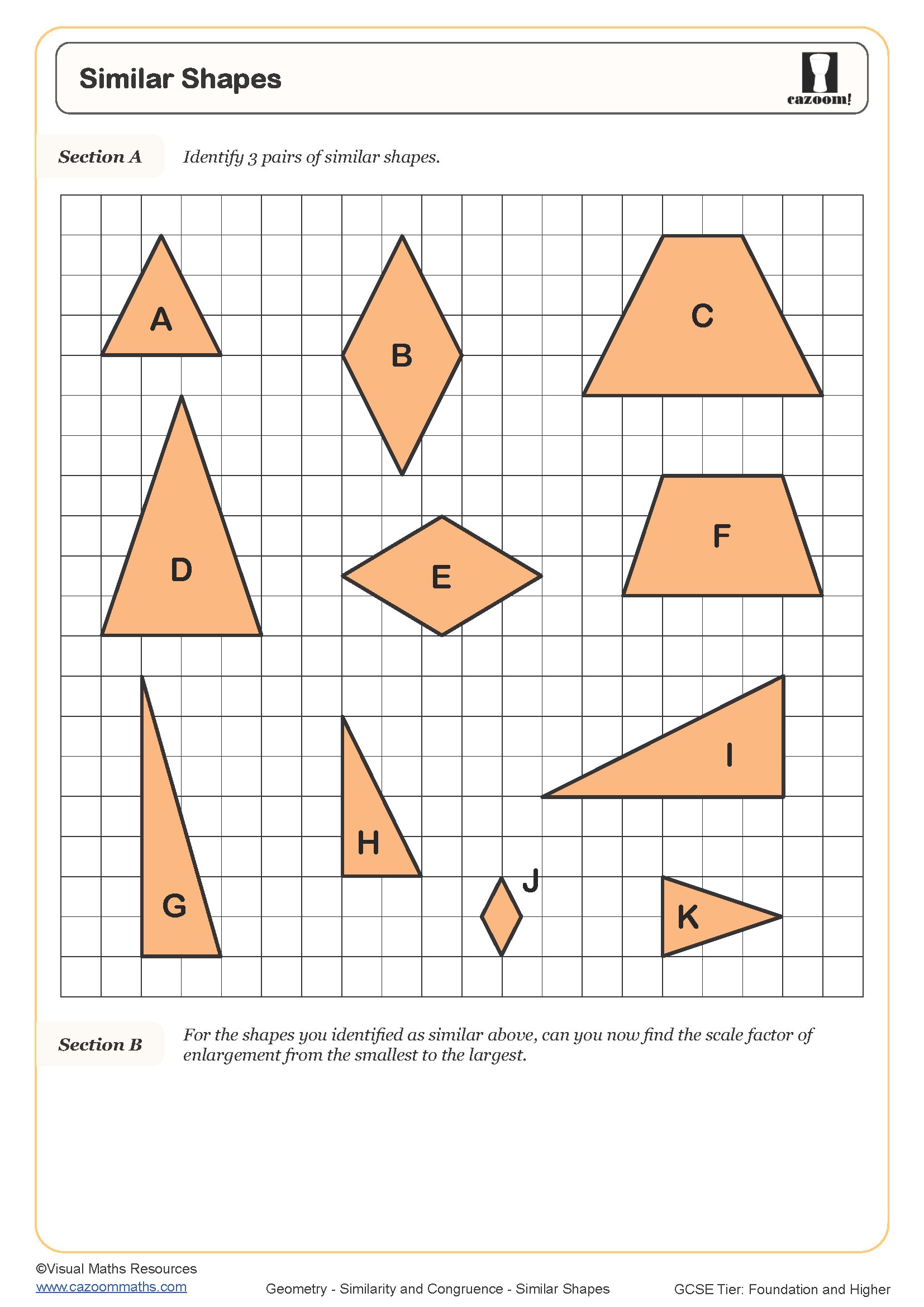
Similar Shapes - Missing Lengths
Year groups: 8, 9
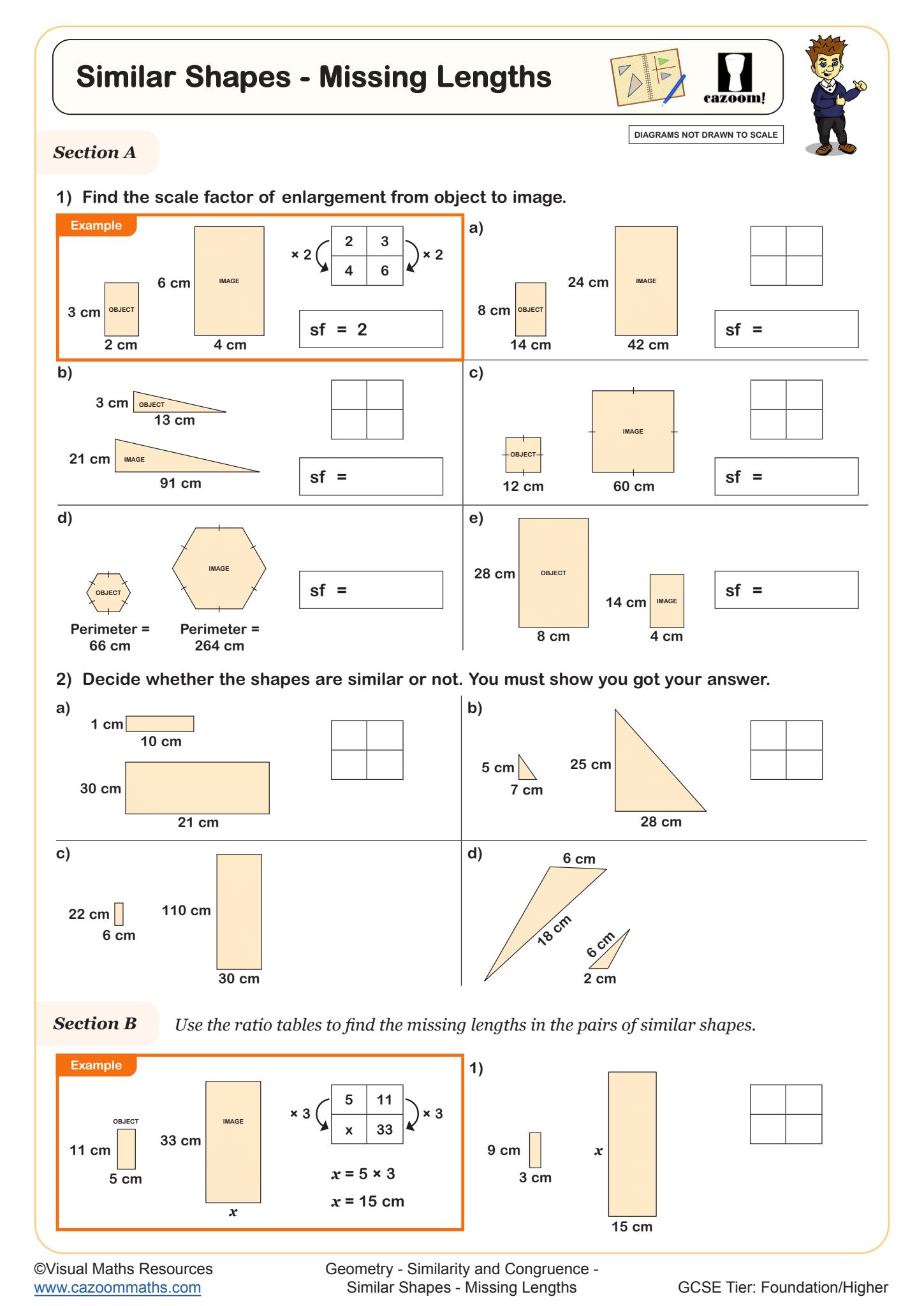
Area and Volume of Similar Shapes (A)
Year groups: 10, 11

Area and Volume of Similar Shapes (B)
Year groups: 10, 11

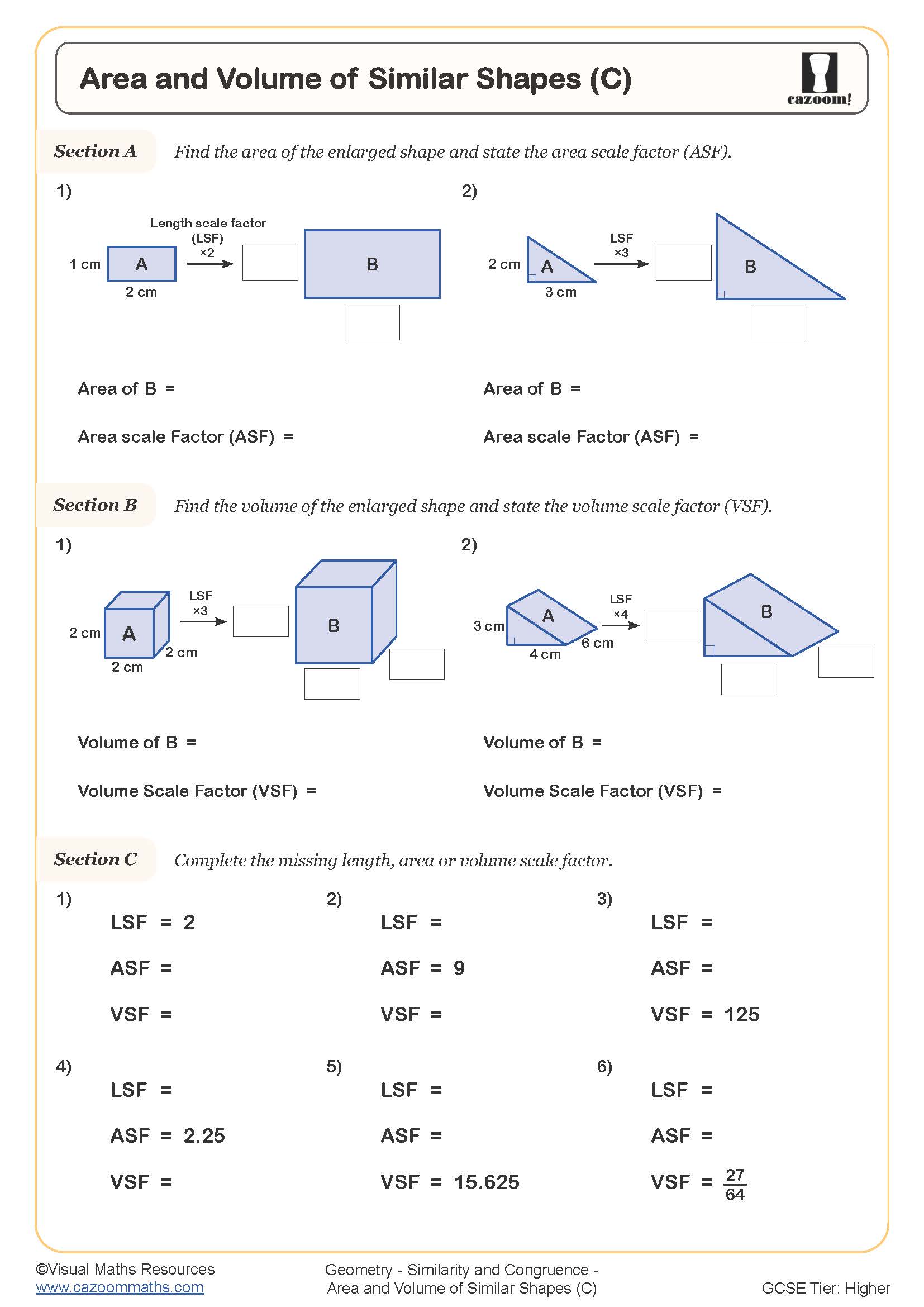
Area and Volume of Similar Shapes (C)
Year groups: 10, 11
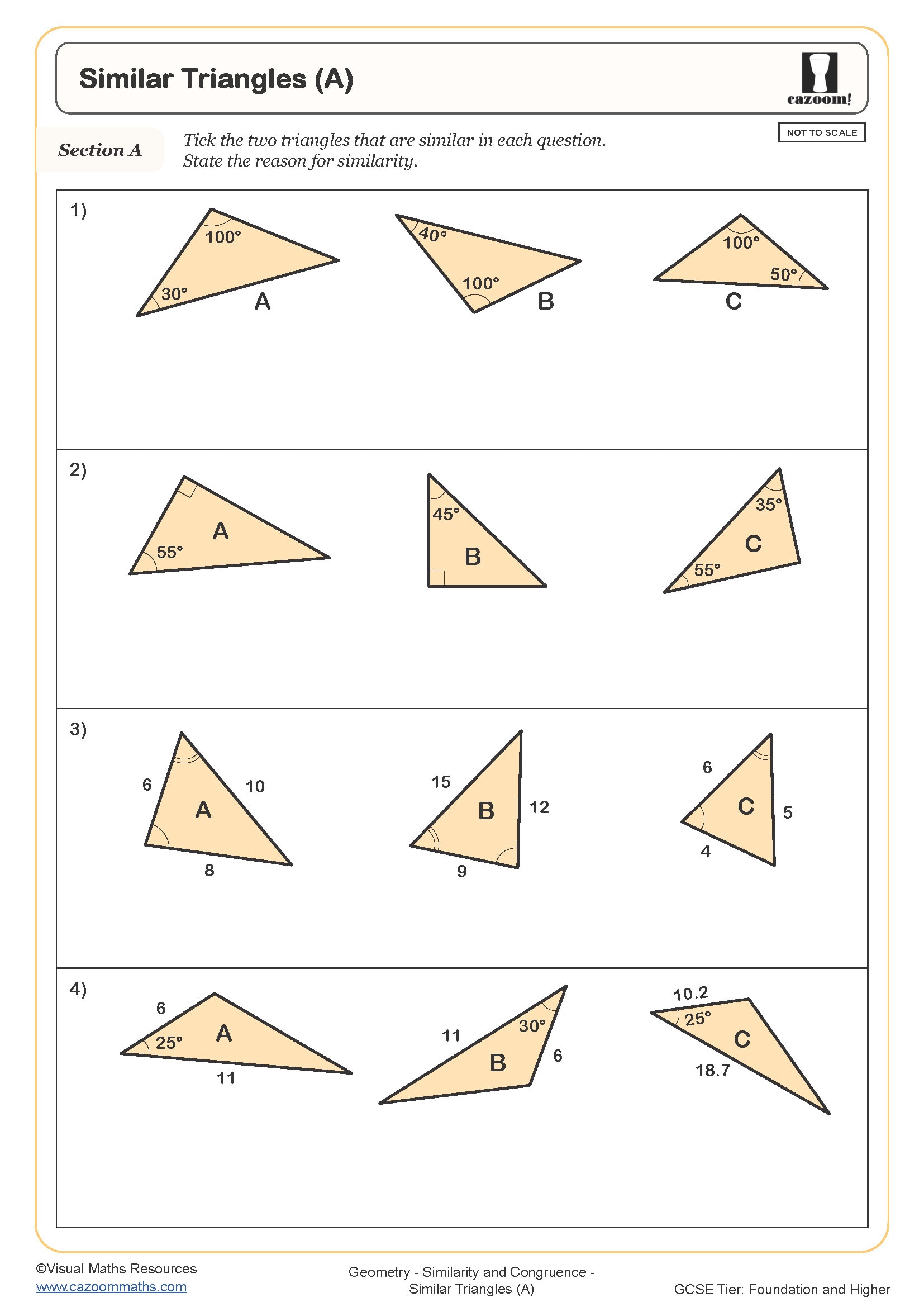
Similar Triangles (A)
Year groups: 10, 11
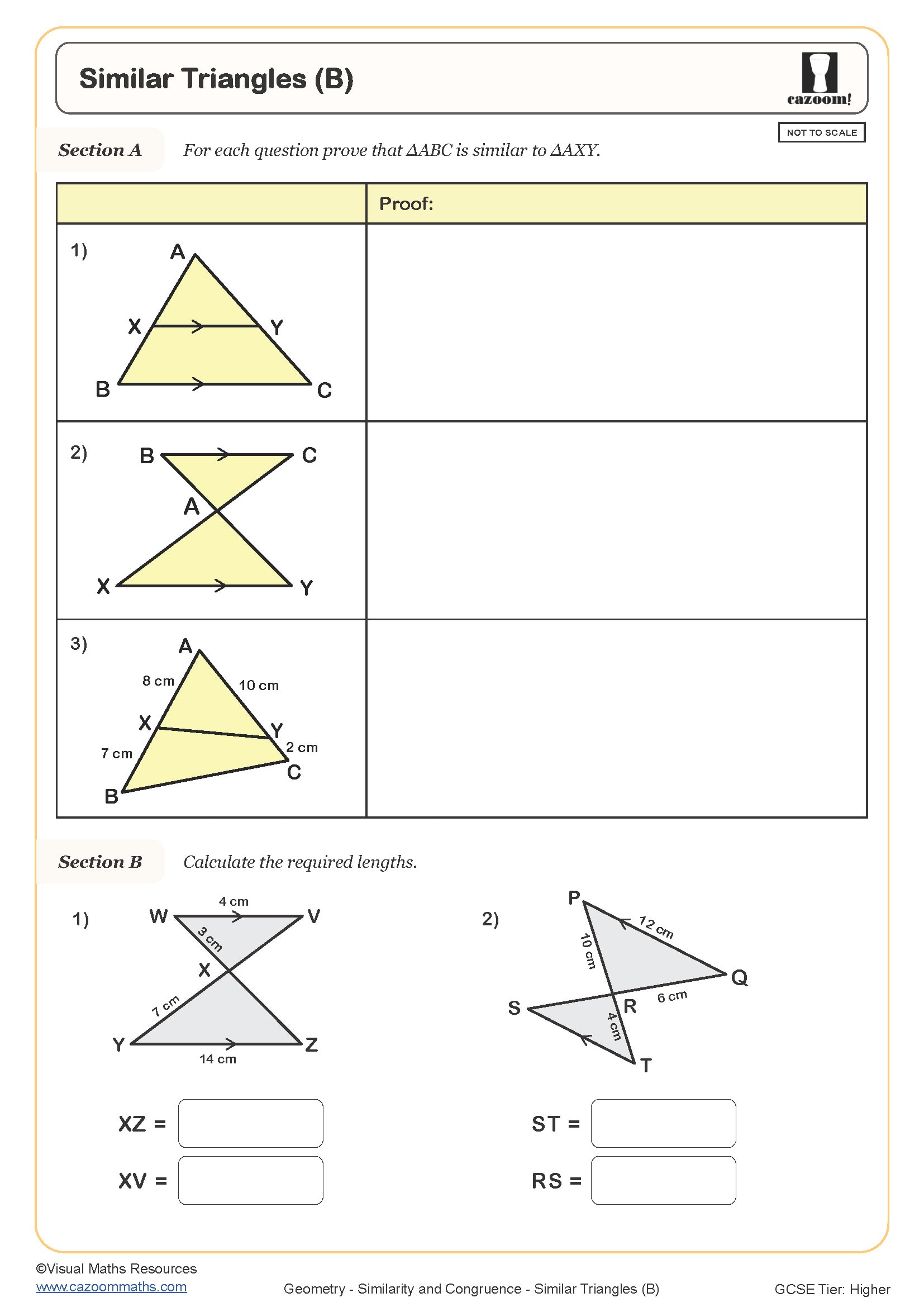
Similar Triangles (B)
Year groups: 10, 11
What are similar shapes in maths?
Similar shapes are figures that have identical angles but different sizes—one is an enlargement of the other. In the National Curriculum, similarity appears formally at KS3 and extends into GCSE, where students must identify similar shapes, calculate scale factors, and apply these relationships to find unknown lengths. The key property is that corresponding sides are in the same ratio, whilst all angles remain equal.
Teachers frequently notice that students confuse similarity with congruence, particularly when shapes are the same size. A common error involves applying scale factors incorrectly—students might add the scale factor to lengths rather than multiplying, or they'll calculate the scale factor but then forget which direction it operates (enlarging versus reducing). Exam questions often present similar triangles nested within larger diagrams, requiring students to identify the similar pair before any calculations begin.
Which year groups study similarity?
These worksheets cover similarity across Year 8, Year 9, Year 10, and Year 11, spanning both KS3 and KS4. At KS3, students begin with recognising similar shapes and calculating simple scale factors, building on their earlier work with ratio and proportion. This foundation work typically starts in Year 8, where the focus remains on straightforward examples with shapes in standard orientations.
By Year 10 and Year 11, similarity becomes more demanding at GCSE level. Students tackle problems involving similar triangles in complex diagrams, area and volume scale factors (which relate to the linear scale factor squared and cubed respectively), and applying similarity to prove geometric results. Higher tier papers regularly feature multi-step similarity problems where students must first establish that shapes are similar before finding multiple unknown values, often within trigonometry or Pythagoras theorem contexts.
How do scale factors work with area and volume?
When two shapes are similar with a linear scale factor of k, their areas relate by k² and their volumes by k³. This relationship stems from how dimensions combine—area involves two dimensions (length × width), whilst volume involves three (length × width × height). Students must square the linear scale factor to find how areas compare, and cube it for volumes. This appears throughout GCSE Higher tier and forms a key discriminator between grades.
This concept connects directly to real-world applications in manufacturing, architecture, and engineering. When companies produce scale models of buildings or vehicles, material costs relate to surface area (paint, cladding), whilst capacity or weight relates to volume. Understanding that doubling all dimensions actually increases volume eightfold explains why larger vehicles aren't simply scaled-up versions of smaller ones—structural requirements change dramatically. Pharmaceutical companies use similar principles when scaling up chemical production from laboratory to industrial quantities, where container volumes grow much faster than their surface areas.
How can these similarity worksheets support classroom teaching?
The worksheets provide structured practice that builds from identifying similar shapes through to multi-step problem-solving involving scale factors and missing lengths. Questions typically progress from straightforward similar pairs to more complex scenarios where students must extract information from composite diagrams or work backwards from areas to find linear dimensions. This scaffolding helps students develop confidence before tackling examination-style questions where similarity might not be immediately obvious.
Many teachers use these resources for targeted intervention with students who struggle to visualise proportional relationships, or as homework following lessons on ratio applications. The complete answer sheets make them valuable for independent study during revision periods, allowing students to self-check their understanding of both method and accuracy. Paired work proves effective when one student identifies the similar shapes whilst the other calculates scale factors, then they swap roles—this encourages discussion about corresponding sides and mathematical reasoning rather than just following procedures.