Volume and Surface Area of Spheres Worksheets
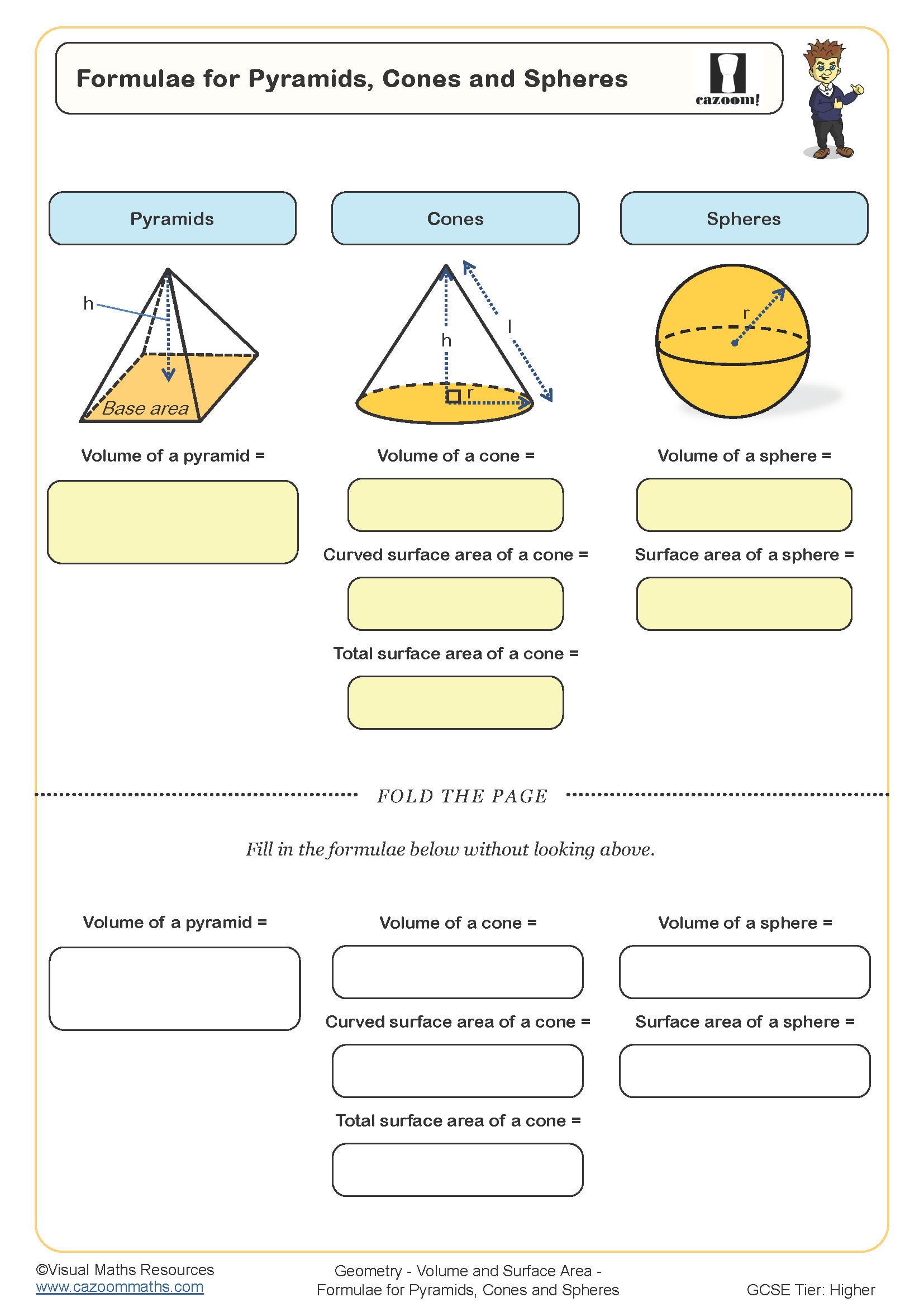
Formulae for Pyramids Cones and Spheres
Year groups: 10, 11
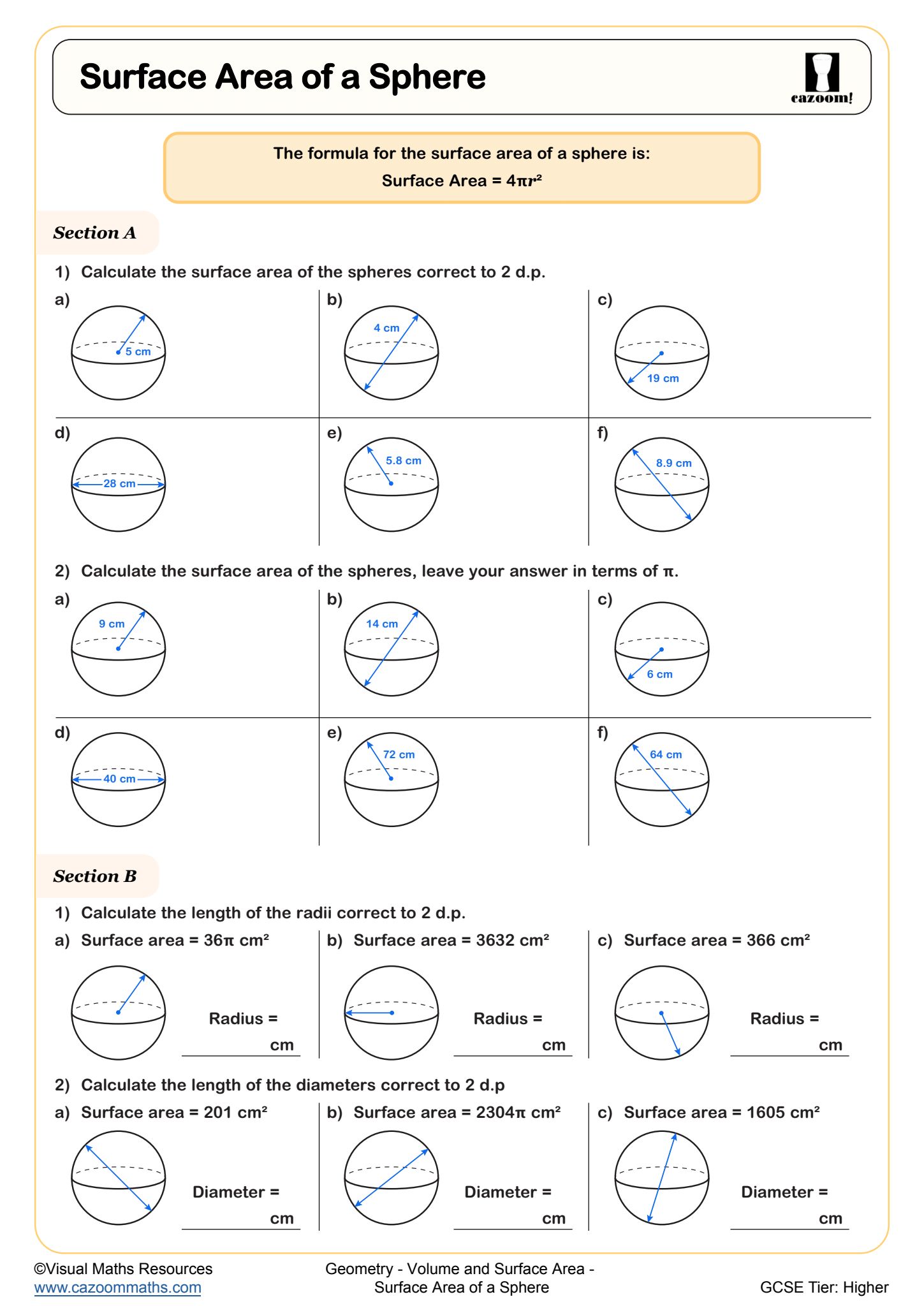
Surface Area of a Sphere
Year groups: 10, 11
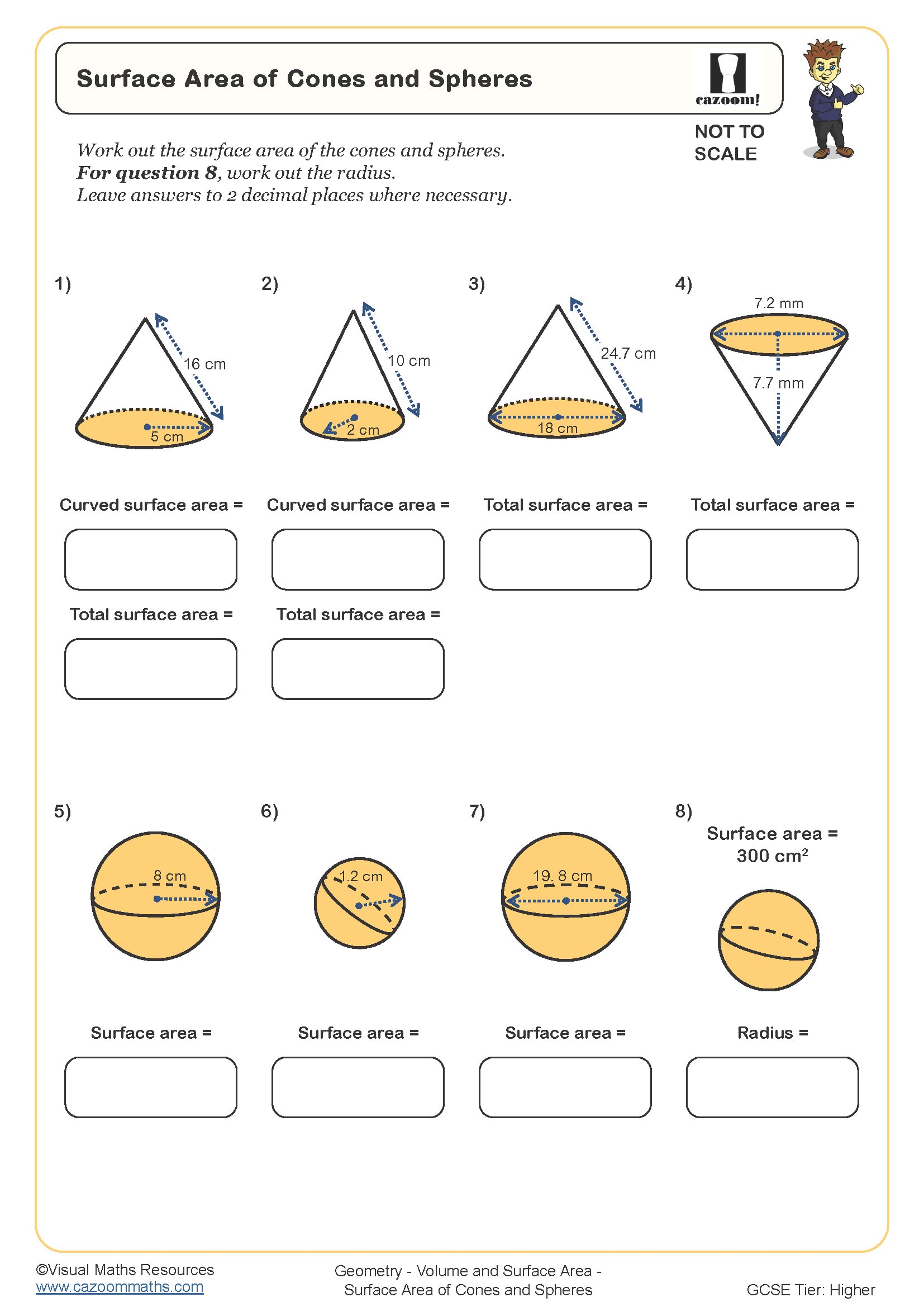
Surface Area of Cones and Spheres
Year groups: 10, 11
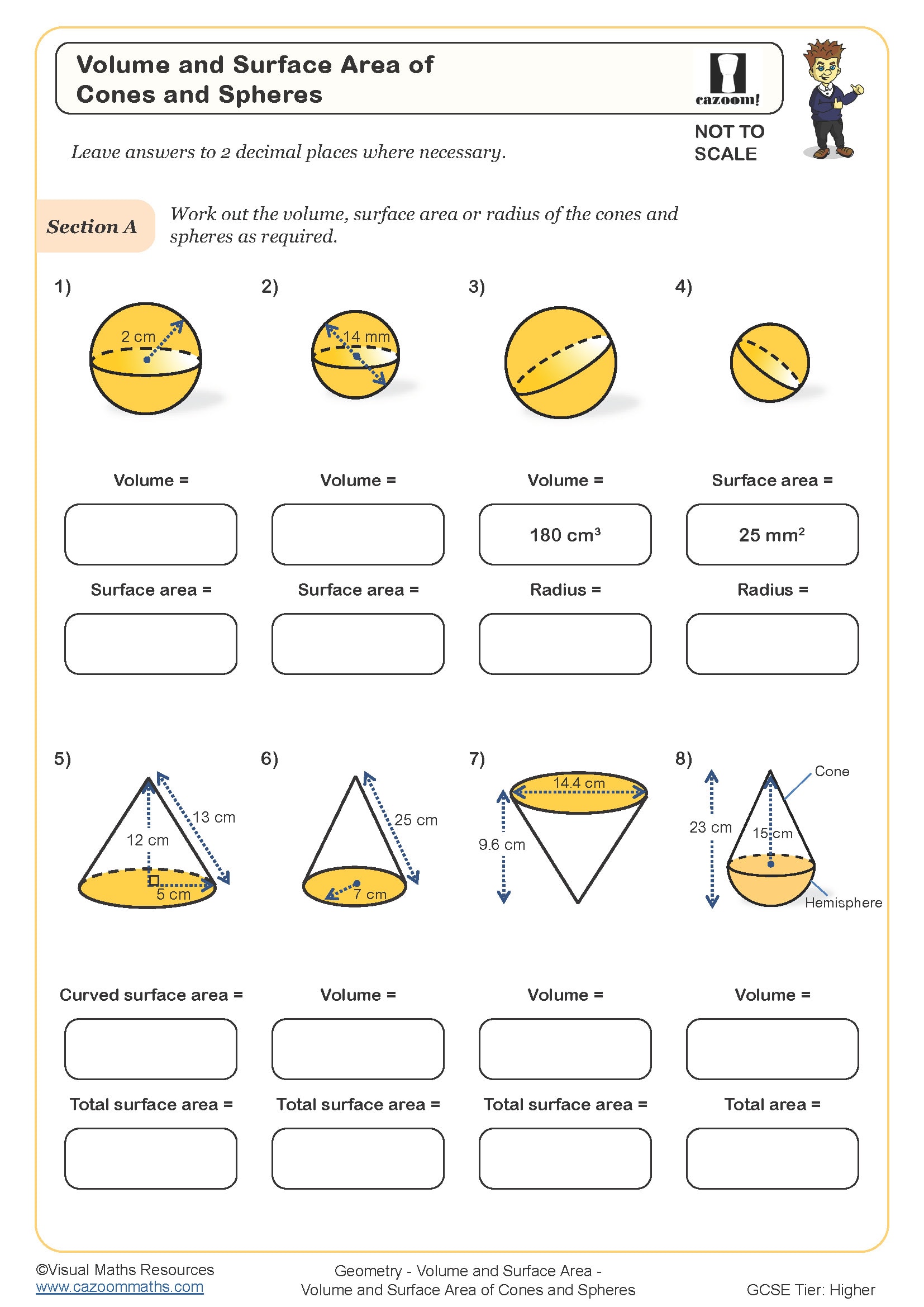
Volume and Surface Area of Cones and Spheres
Year groups: 10, 11
Volume of a Sphere
Year groups: 10, 11

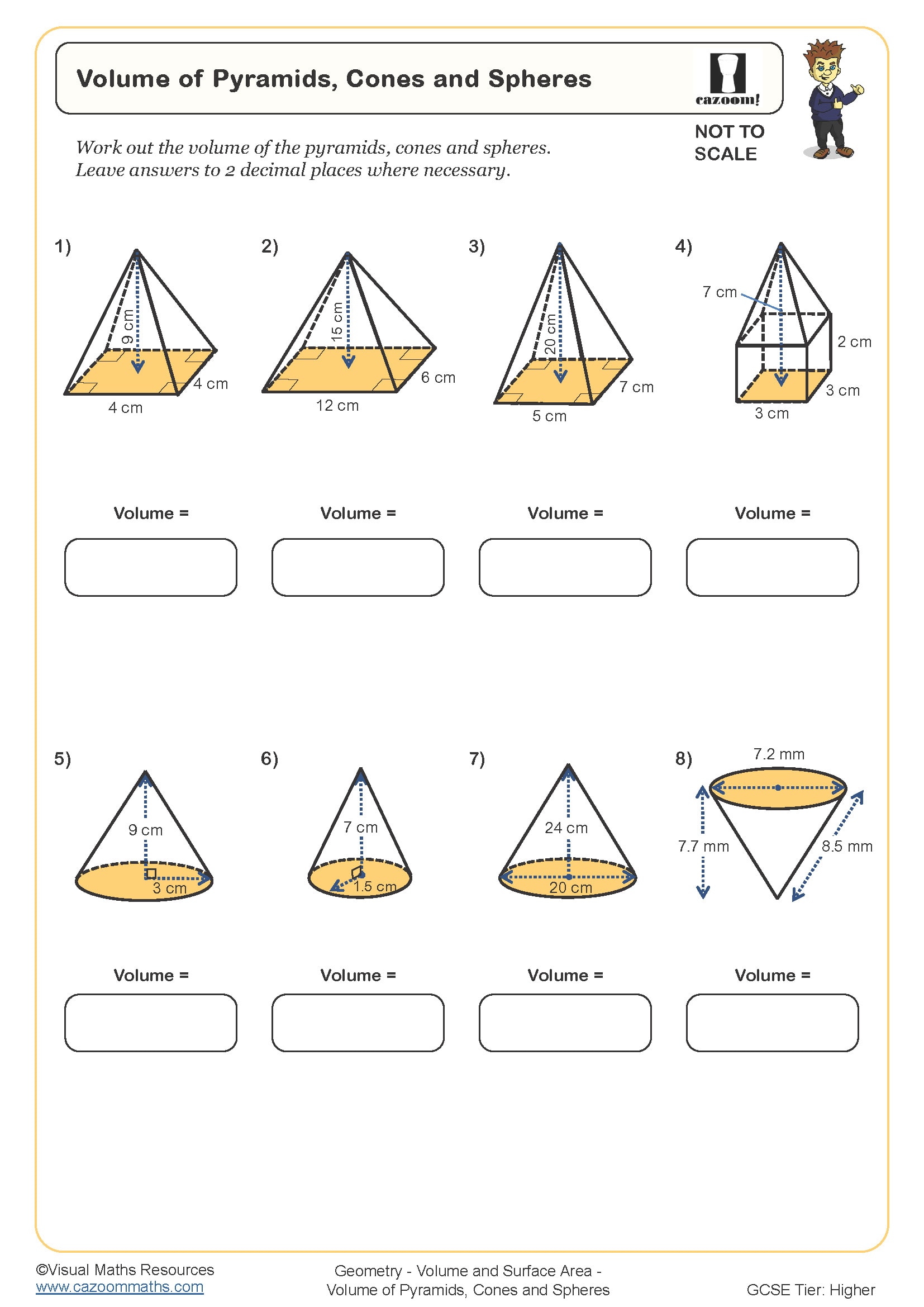
Volume of Pyramids Cones and Spheres
Year groups: 10, 11
All worksheets are created by the team of experienced teachers at Cazoom Maths.
What formulas do students need for volume and surface area of spheres?
Students need two core formulas: volume of a sphere is V = 4/3πr³ and surface area is SA = 4πr², where r represents the radius. At GCSE level, exam questions expect students to recall these formulas from memory, as they typically aren't provided on formula sheets. The worksheets include both exact answers in terms of π and decimal approximations, helping students understand when each form is appropriate.
A frequent error occurs when students apply the surface area formula to volume questions or forget the fraction 4/3 entirely, writing V = πr³ instead. Teachers report that students who struggle to remember which formula is which benefit from noting that volume (a 3D measurement) involves r³, while surface area (covering the outside) involves r². Exam mark schemes penalise formula errors heavily, so securing these formulas early in Year 10 proves valuable.
Which year groups study volume and surface area of spheres?
Volume and surface area of spheres appears in the KS4 curriculum for Year 10 and Year 11 students as part of the geometry and measures strand. This topic builds on earlier work with circles, where students learned to calculate circumference and area using π. The National Curriculum requires students to calculate surface areas and volumes of spheres at GCSE level, appearing on both Foundation and Higher tier papers.
The progression across these year groups typically moves from applying formulas with given radii to more complex problems involving diameters, hemispheres, and composite 3D shapes. Year 11 worksheets often include questions where students must find missing dimensions when volume or surface area is given, requiring algebraic manipulation and cube root calculations. Questions involving spheres within cylinders or cubes also appear at Higher tier, testing spatial reasoning alongside formula application.
How do you calculate the surface area of a hemisphere?
Calculating the surface area of a hemisphere requires students to find half the sphere's curved surface area, then add the flat circular base. Using SA = 4πr² for the full sphere, the curved surface becomes 2πr², and the circular base contributes πr², giving a total of 3πr² for a hemisphere. Students frequently forget to include the flat circular face, calculating only the curved portion and losing marks in exams.
This calculation appears in real-world engineering contexts, particularly when designing storage tanks and pressure vessels. The Millennium Dome in London features a hemispherical structure where surface area calculations determined the amount of fabric needed for the roof. Similarly, architects calculating materials for planetarium domes or sports arena roofs use these principles. Understanding hemispheres also connects to manufacturing costs in industries producing spherical containers, where cutting a sphere in half creates two usable hemispheres with different surface areas than solid spheres.
How do these worksheets help students prepare for GCSE questions on spheres?
The worksheets provide structured practise moving from single-step formula application to multi-step problems that mirror GCSE question styles. Students encounter questions requiring them to convert between diameter and radius, work with exact values involving π, and calculate measurements for composite shapes that combine spheres with other solids. Worked examples demonstrate the standard method examiners expect, including showing substitution into formulas and maintaining accuracy throughout calculations.
Many teachers use these resources for targeted revision when students struggle specifically with 3D shapes, as sphere questions often appear alongside cylinders and cones in exam papers. The worksheets work well for homework following initial teaching, allowing students to consolidate formula recall independently. Some teachers set them as paired activities where students check each other's formula selection before calculating, addressing the common error of mixing up volume and surface area formulas. The answer sheets enable students to identify where calculation errors occur, whether in formula recall, handling π, or applying powers correctly.