KS3 Bearings Scale and Loci Worksheets
What are bearings in KS3 maths?
Bearings are three-figure angles measured clockwise from north, used to describe direction precisely. In the KS3 curriculum, students learn to measure and draw bearings using a protractor, always writing them with three digits (such as 045° or 215°) and understanding that 000° and 360° both represent north. This sits within the geometry strand and connects to map reading skills taught in geography.
Students commonly lose marks when they measure anticlockwise instead of clockwise, or when they write bearings as two digits (such as 45° instead of 045°). Many teachers find that providing diagrams with north clearly marked at multiple positions helps reinforce the correct starting point. Exam questions often require students to work backwards from a bearing to find a return bearing, which requires subtracting from 360° or adding 180°, depending on the angle.
Which year groups study bearings, scale and loci?
These worksheets cover Year 7, Year 8 and Year 9, reflecting where bearings, scale and loci appear in the KS3 National Curriculum. Most schools introduce basic bearings in Year 7 or 8, with scale drawings often taught alongside ratio work. Loci typically appear in Year 8 or 9 as students develop their compass and construction skills within the geometry curriculum.
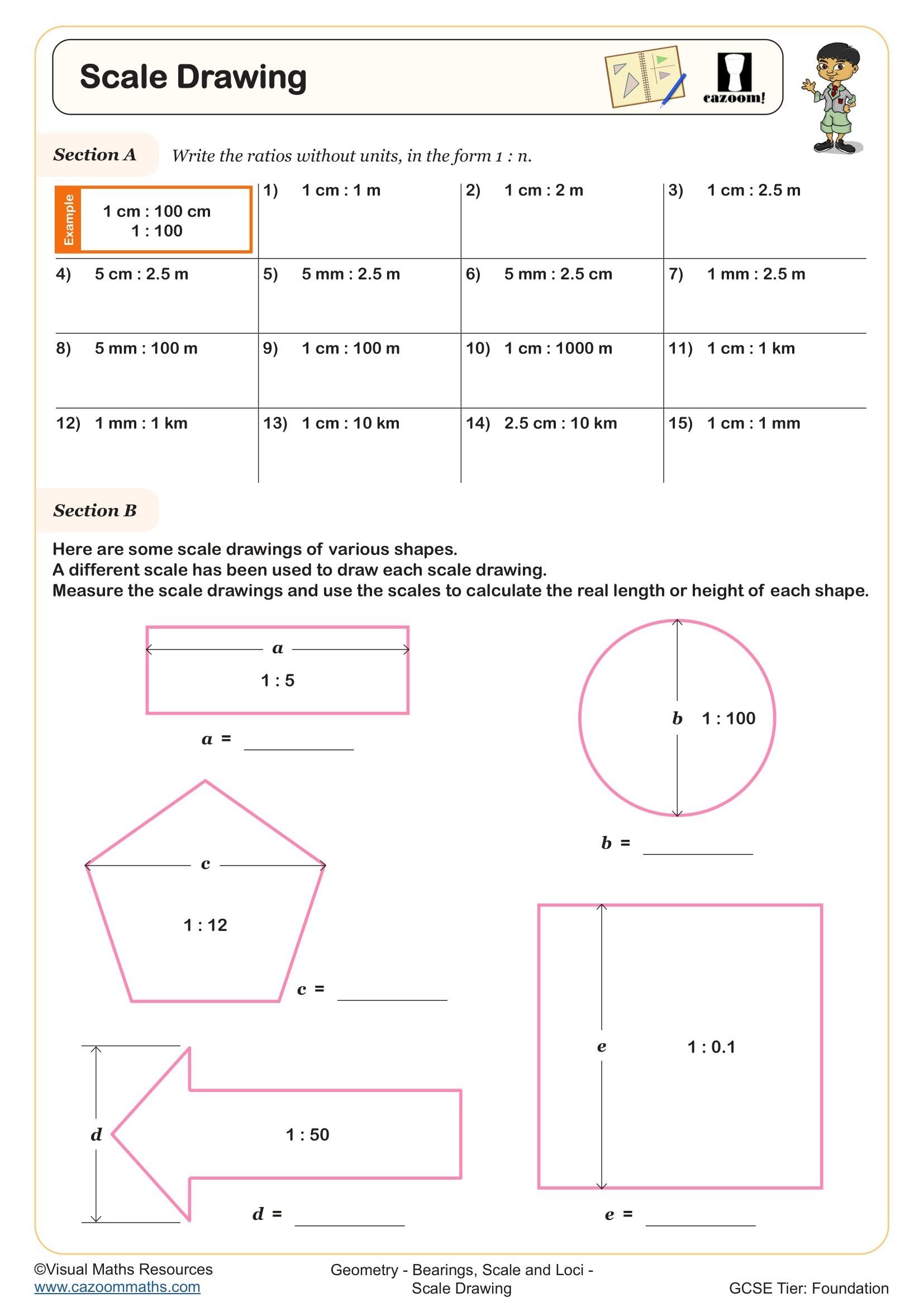
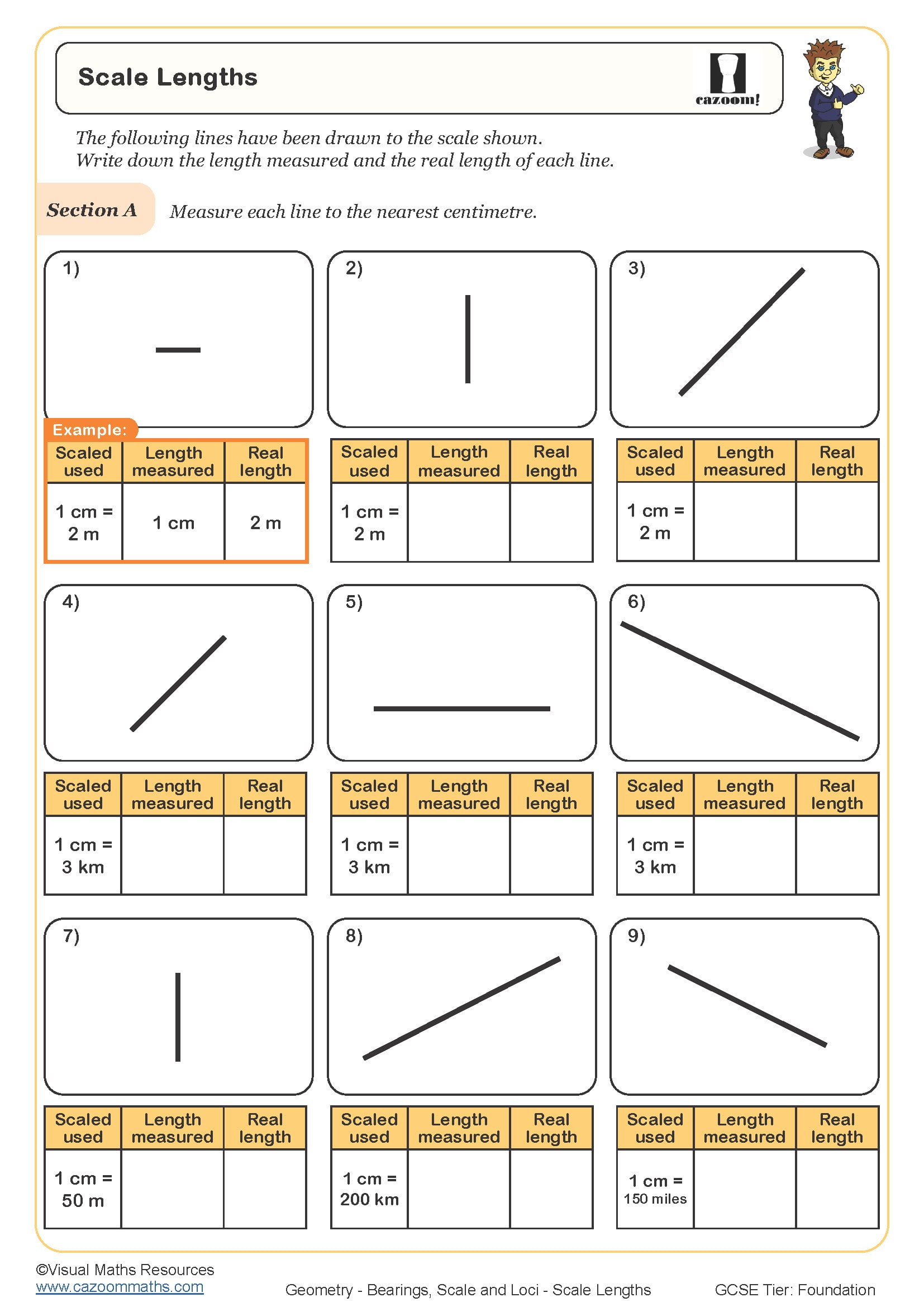
The progression moves from measuring and drawing simple bearings to solving multi-step problems involving scale diagrams and distance calculations. Year 9 work typically combines these skills, asking students to use bearings on scale drawings or construct loci that satisfy bearing conditions. Teachers frequently sequence this topic after ratio and proportion work, since interpreting scale requires understanding that distances are multiplied by a constant scale factor, and this connection strengthens both skill areas.
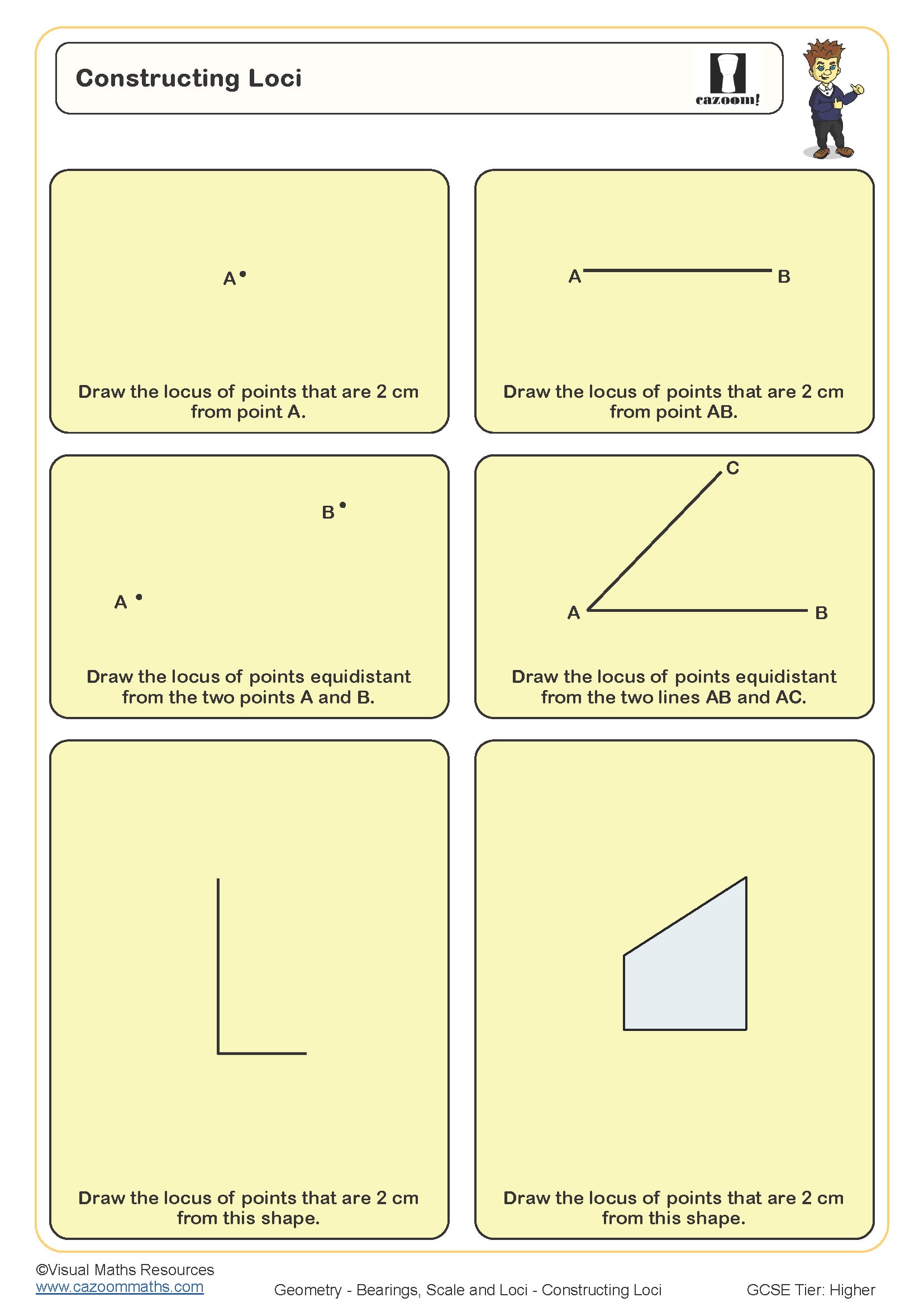
How do you construct loci accurately?
Constructing loci means drawing all the points that satisfy a given condition, using compasses and rulers to create accurate geometric shapes. Common loci include the set of points equidistant from a fixed point (a circle), equidistant from two points (a perpendicular bisector), or equidistant from two lines (an angle bisector). Students need to keep their compass point firmly in place and draw smooth arcs without adjusting the radius.
Loci construction appears in real-world contexts including mobile phone mast positioning, where engineers determine coverage areas as circular loci from transmission points. In archaeology, excavation sites are often defined using loci based on distances from known landmarks. Air traffic control uses loci principles when defining safe zones around airports, where aircraft must remain certain distances from the runway or other planes. These applications show students why precision in construction matters beyond the classroom.
How should teachers use these bearings and loci worksheets?
The worksheets provide structured practice with questions that increase in complexity, allowing students to build confidence before tackling problems that combine bearings, scale and loci together. Each question requires careful drawing and measurement, so students develop the patience and precision needed for accurate geometric work. The answer sheets show the expected constructions with measurements clearly marked, which helps teachers identify where errors occurred.
Many teachers use these worksheets during intervention sessions for students who struggle with spatial reasoning or accurate measuring. They work effectively as homework following initial teaching, giving students time to work carefully with their own equipment. Paired work can be valuable, with one student dictating a bearing or scale factor whilst their partner draws, then swapping roles. This approach builds mathematical communication alongside technical skills.