KS3 Calculator Methods Worksheets
All worksheets are created by the team of experienced teachers at Cazoom Maths.
What calculator skills do KS3 students need to master?
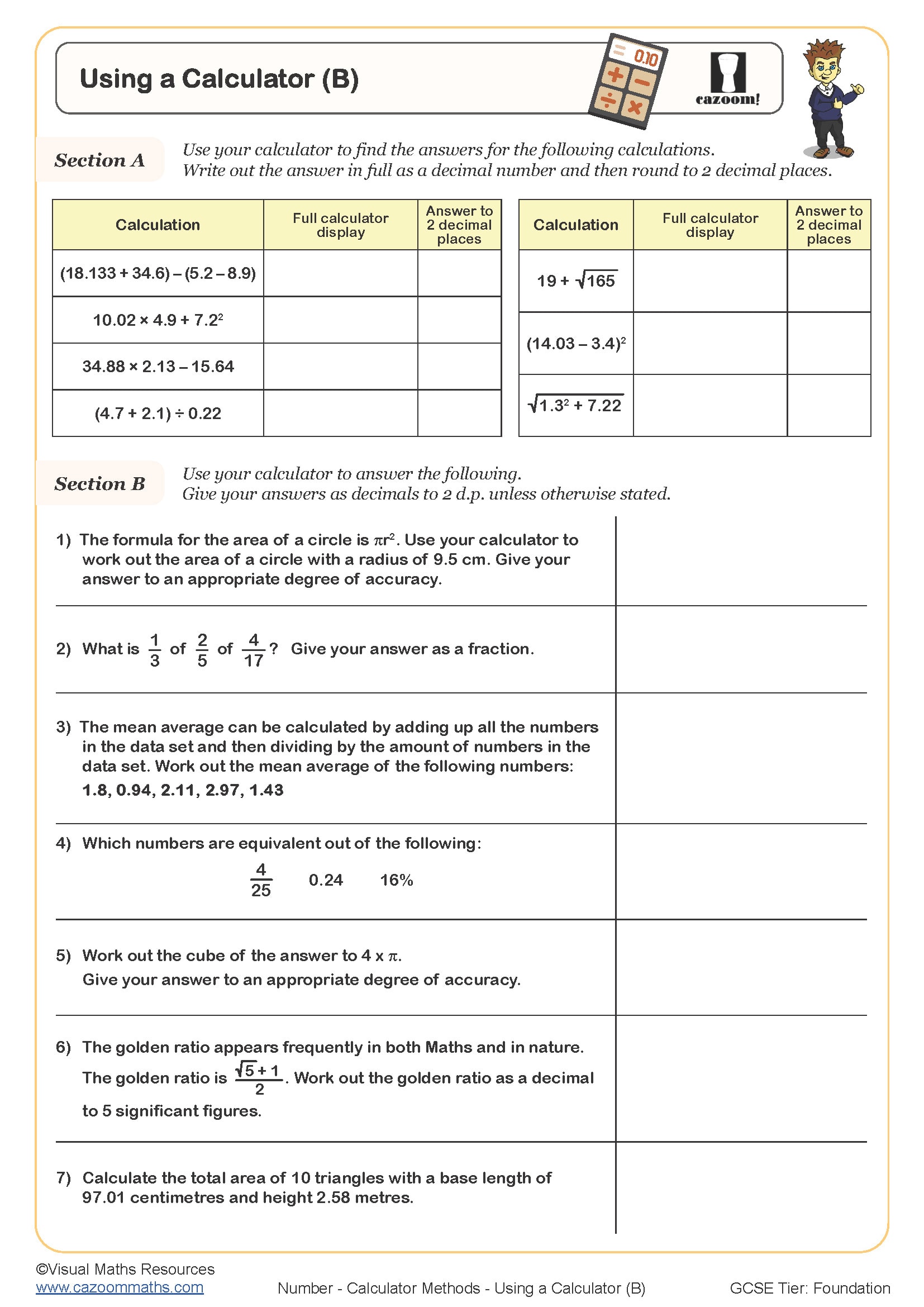
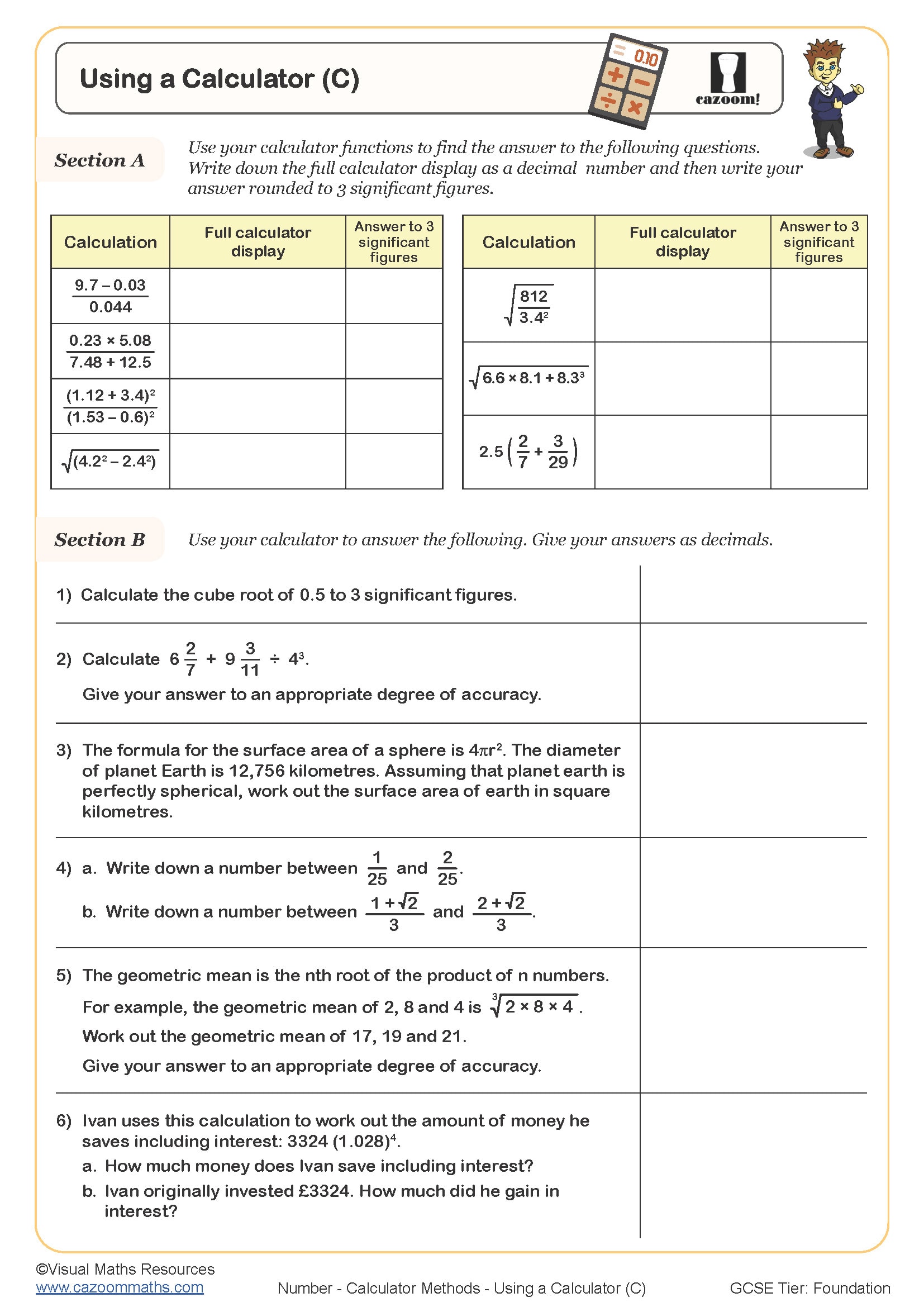
KS3 students need to develop competence with both basic four-function calculators and scientific calculators, including entering calculations with brackets, using memory functions, working with powers and roots, and interpreting displays correctly. The National Curriculum expects Year 7, 8, and 9 students to use calculators strategically for complex calculations whilst maintaining number sense to spot unreasonable answers.
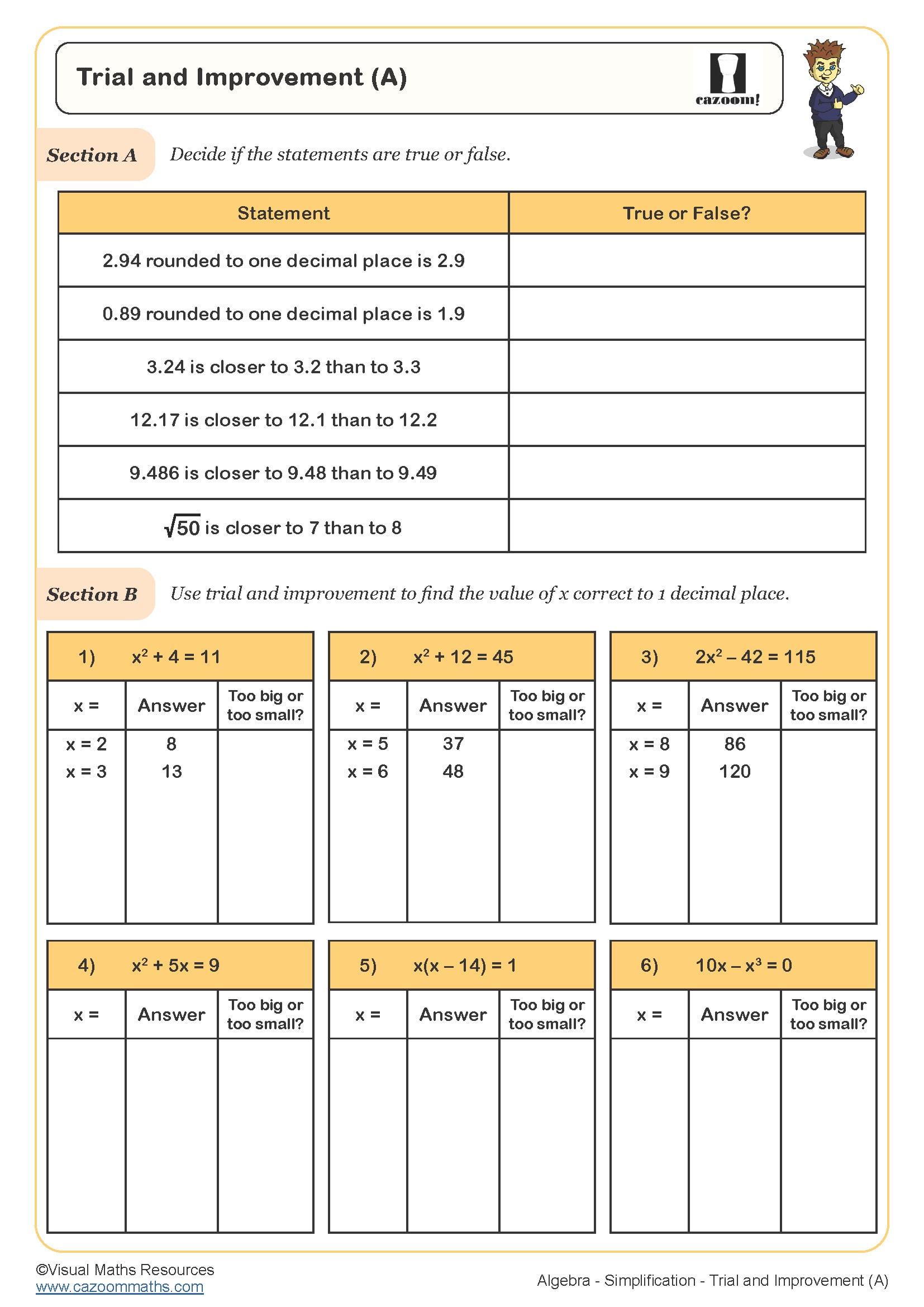
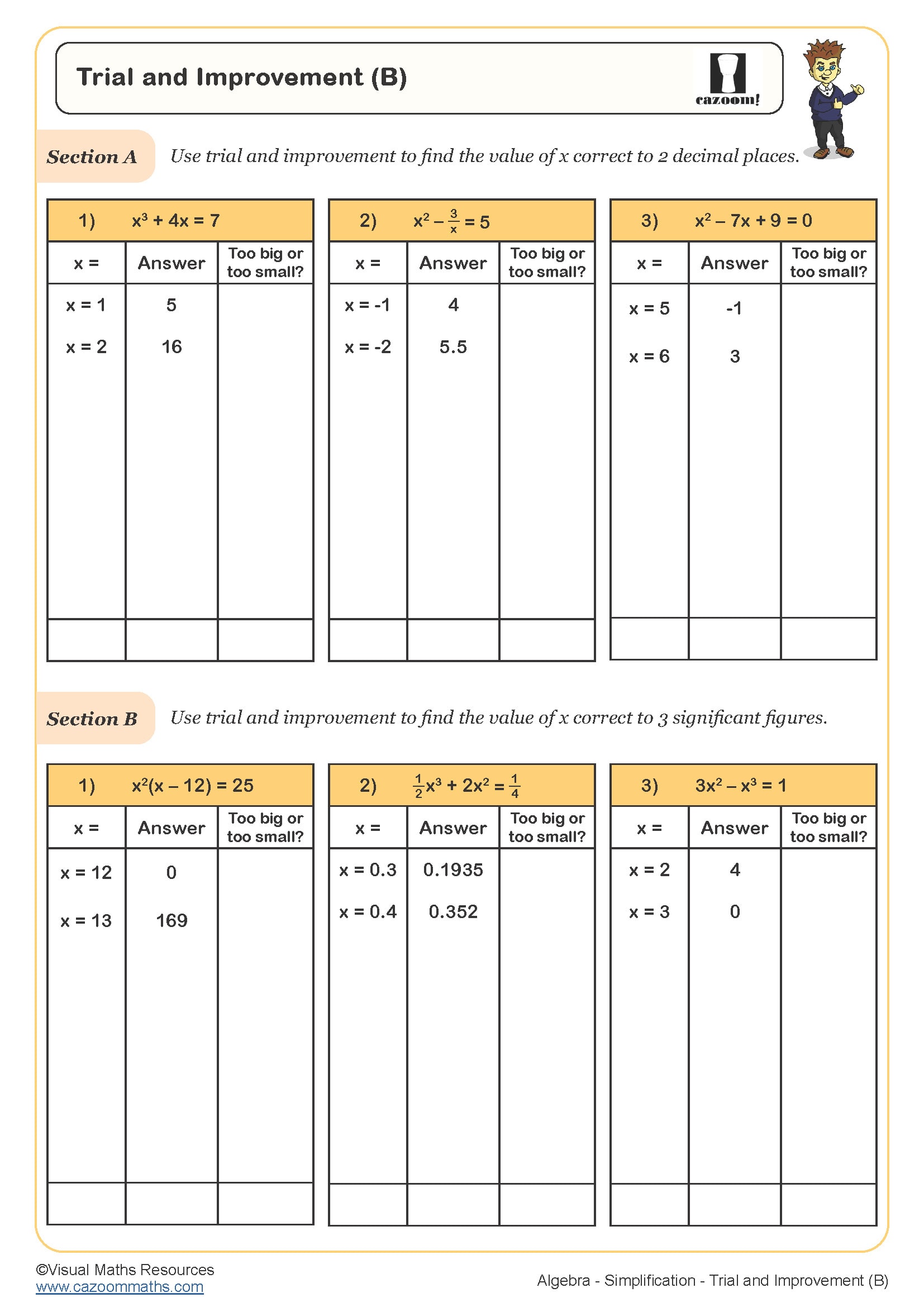
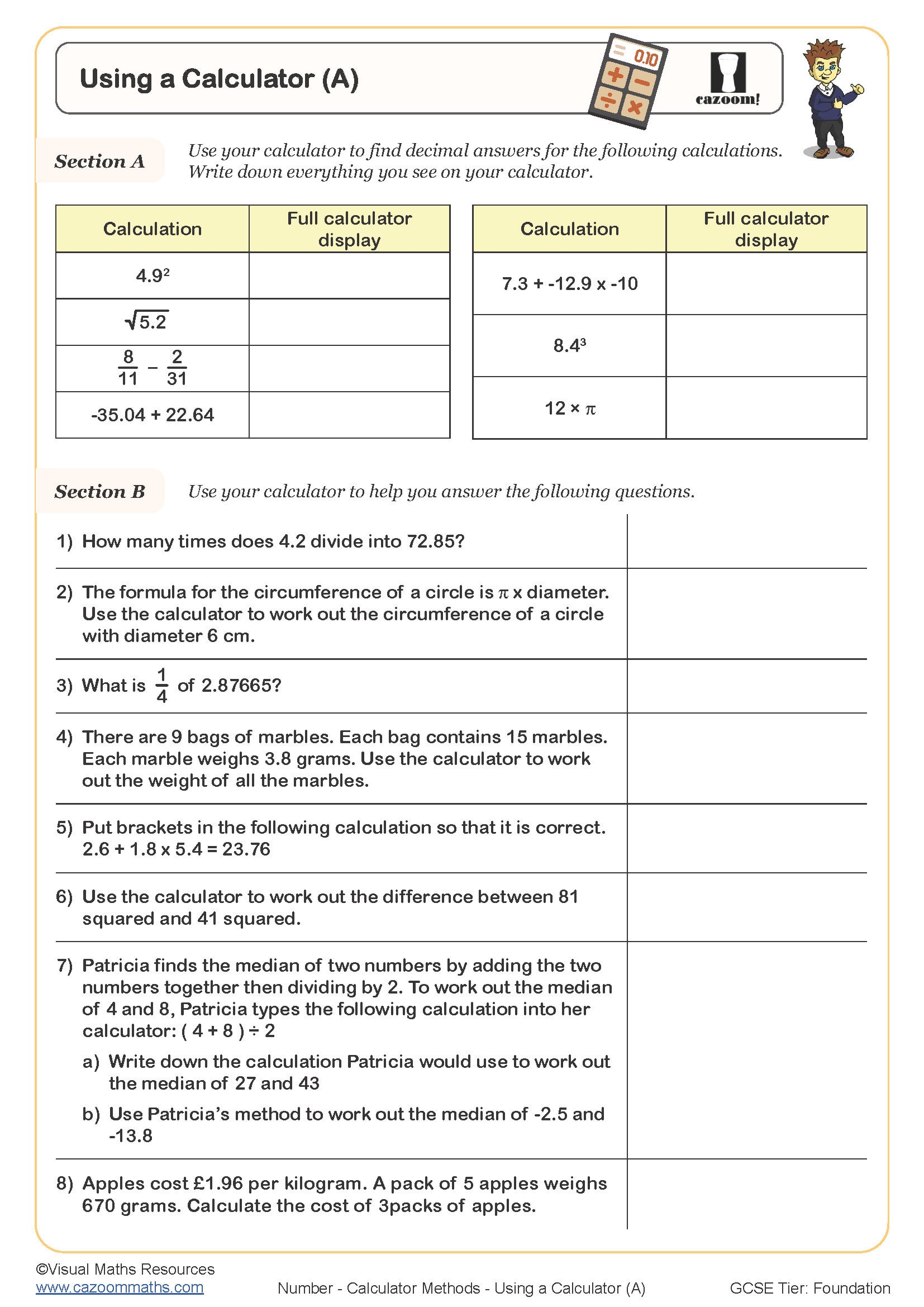
Students frequently lose marks when they fail to use bracket keys properly in multi-step calculations, particularly when working with fractions or mixed operations. For example, when calculating 48 ÷ (3 + 5), many students enter 48 ÷ 3 + 5 and arrive at 21 instead of 6. Teachers find that explicit practice with bracket notation alongside calculator work helps students connect written mathematics to calculator input sequences.
Which year groups use calculator methods worksheets?
Calculator methods appear throughout KS3, with dedicated practice in Year 7, Year 8, and Year 9 as students encounter increasingly complex numerical problems. Year 7 typically focuses on basic calculator operations, interpreting displays, and using calculators alongside estimation to check reasonableness. By Year 8 and 9, students apply calculator methods to standard form, trigonometry, and multi-step problems involving multiple operations.
Progression across KS3 moves from straightforward calculations requiring correct order of operations to sophisticated problems where students must decide which calculator functions to use. Year 9 work often involves using the power key for indices, working with standard form buttons, and interpreting calculator displays showing very large or very small numbers, preparing students for GCSE calculator paper demands where efficient calculator use saves valuable exam time.
How do students work with standard form on calculators?
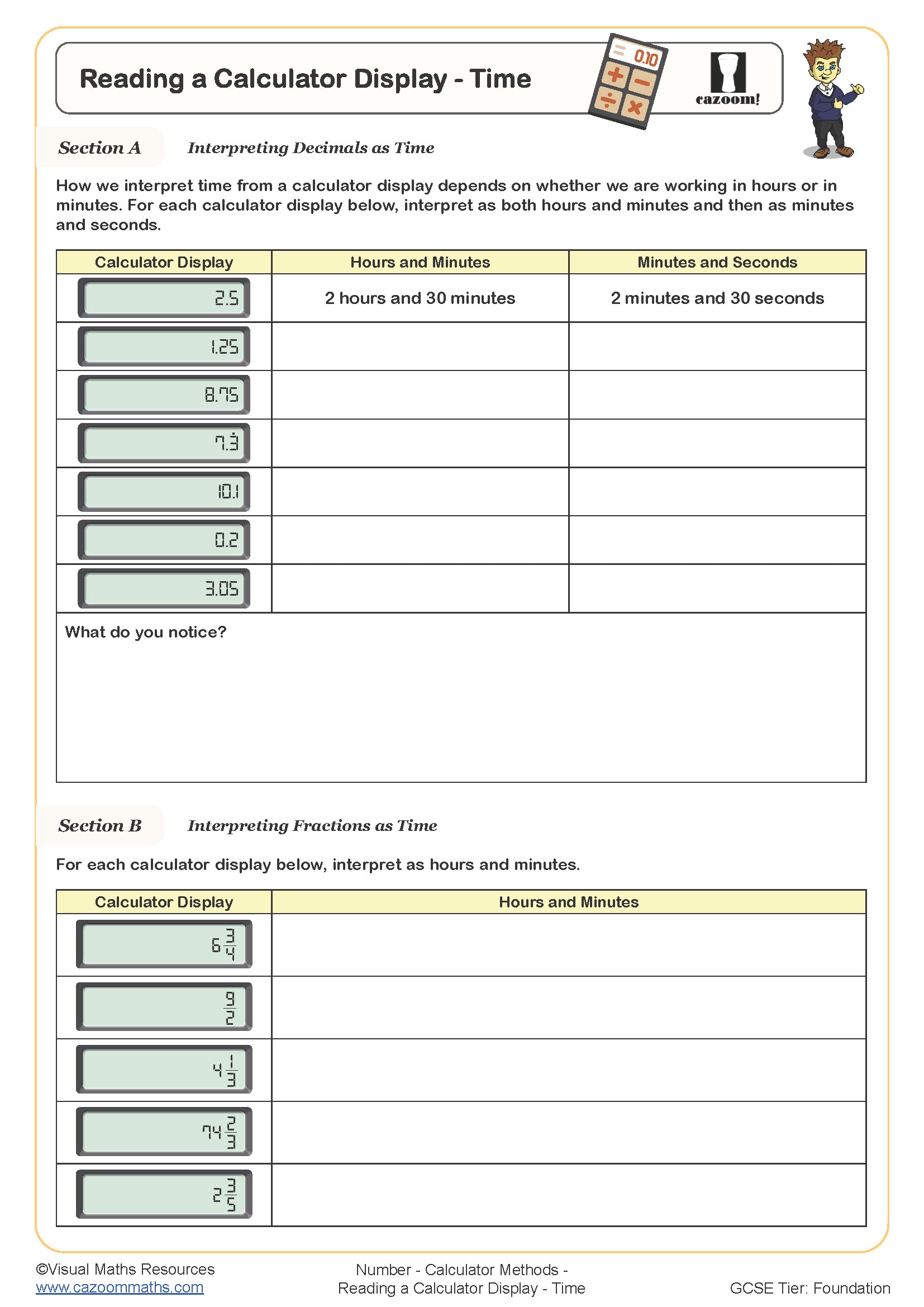
Standard form calculations require students to understand how calculators display numbers in the format a × 10ⁿ, typically shown as '3.2 E 5' or '3.2 ₁₀' depending on the calculator model. Students learn to enter standard form using the EXP or ×10ˣ button rather than multiplying by powers of 10 separately, which introduces rounding errors and wastes time. Teachers observe that students commonly confuse the EXP button with the power key, entering 10 then using the power function instead.
Standard form calculator skills connect directly to scientific contexts where students encounter astronomical distances, atomic scales, or data storage capacities. In physics, calculating the energy of photons or distances between planets requires confident manipulation of standard form on calculators. Engineers and scientists use standard form notation constantly, making this calculator skill essential preparation for STEM pathways where numerical values span many orders of magnitude beyond what standard notation can practically represent.
How should teachers use these calculator methods worksheets?
The worksheets provide structured practice that moves from basic calculator operations through to complex multi-step problems, with questions designed to expose common input errors and misinterpretations. Many worksheets include problems where students must compare their calculator answer with an estimate, building the habit of checking reasonableness. Complete answer sheets allow students to self-check their calculator work and identify whether errors stem from incorrect button sequences or misreading displays.
These resources work effectively as starter activities to refresh calculator skills before tackling topic-specific content like Pythagoras or trigonometry that demands efficient calculator use. Teachers use them for intervention with students who struggle to translate written mathematics into correct calculator sequences, or as homework to build fluency outside lesson time. Paired work where students verbalise their button presses to a partner helps identify where misconceptions about order of operations or bracket use occur, making invisible calculator work visible for correction.