KS3 Constructions Worksheets
What Are the Key Construction Skills Students Need at KS3?
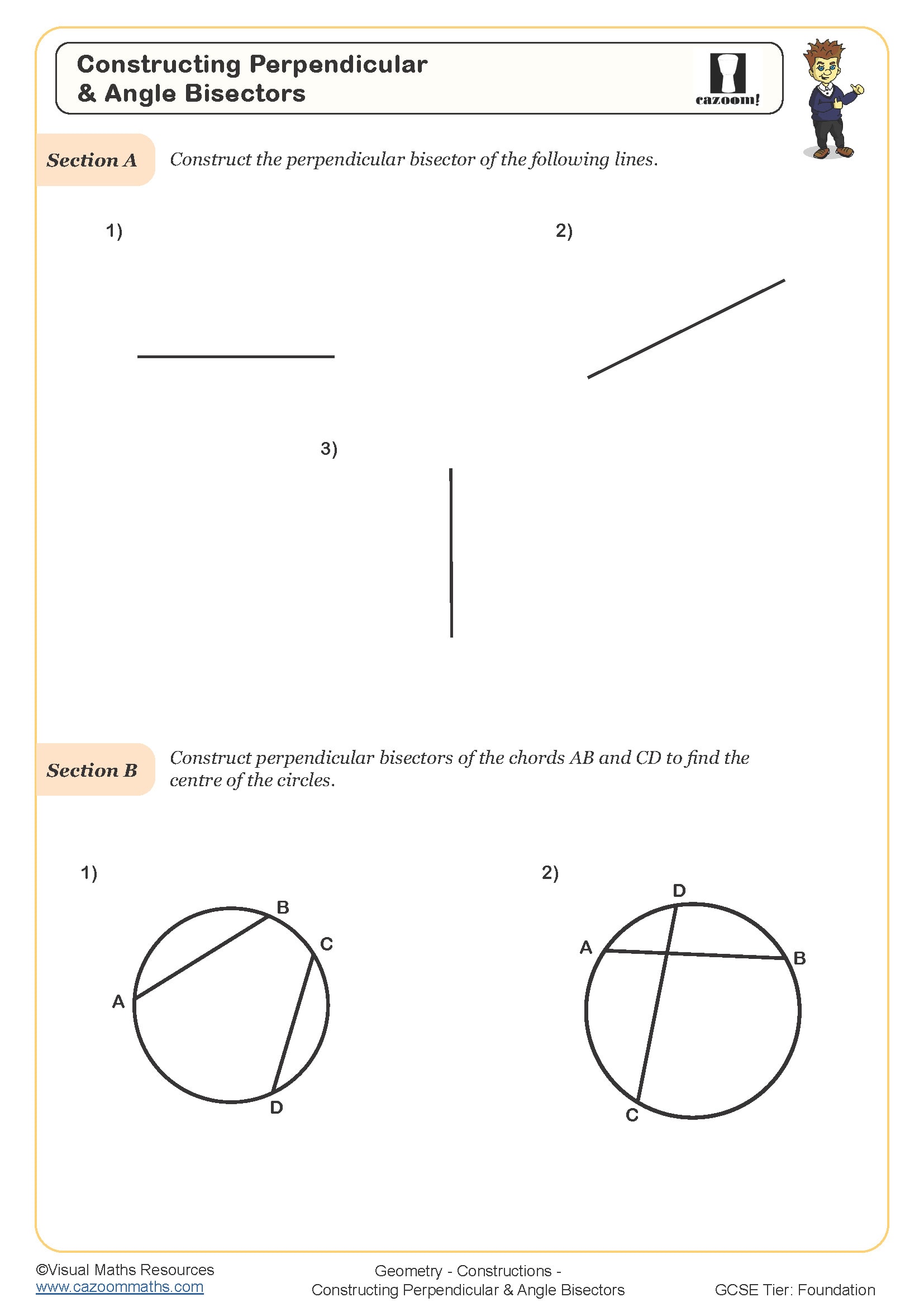
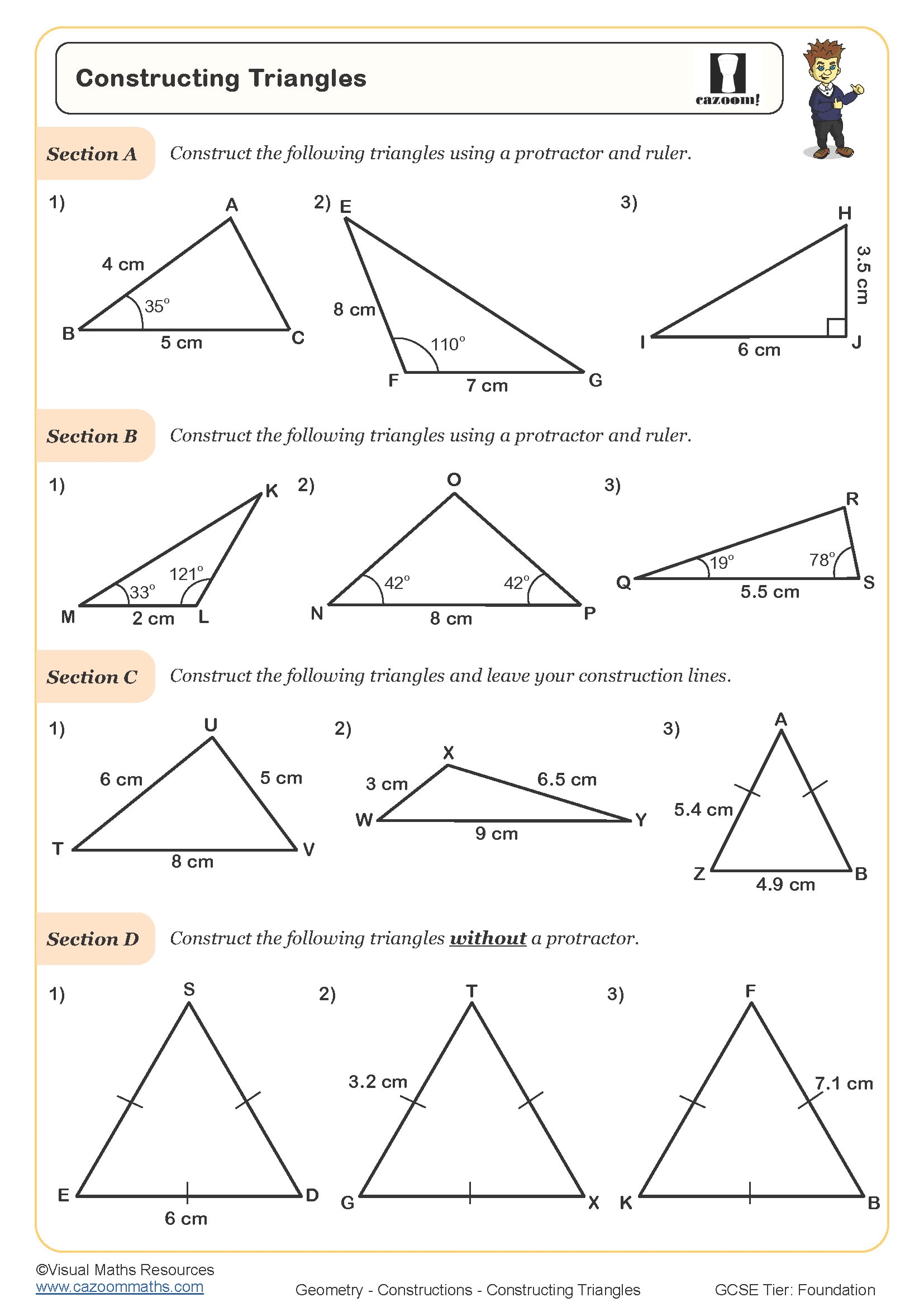
At Key Stage 3, students must master five fundamental constructions: perpendicular bisector of a line segment, angle bisector, perpendicular from a point to a line, 60-degree angle, and constructing triangles from given measurements. The National Curriculum expects students to use only a compass and straight edge, building understanding of why these methods work geometrically rather than simply measuring with a protractor.
A common error occurs when students erase their construction arcs to make diagrams look neater, removing the evidence that proper methods were used. Teachers consistently observe that students who understand compass radius remains constant throughout a construction produce more accurate results than those who adjust the compass repeatedly. This precision becomes particularly important for inscribed shapes within circles, where multiple construction lines must intersect exactly.
Which Year Groups Study Constructions?
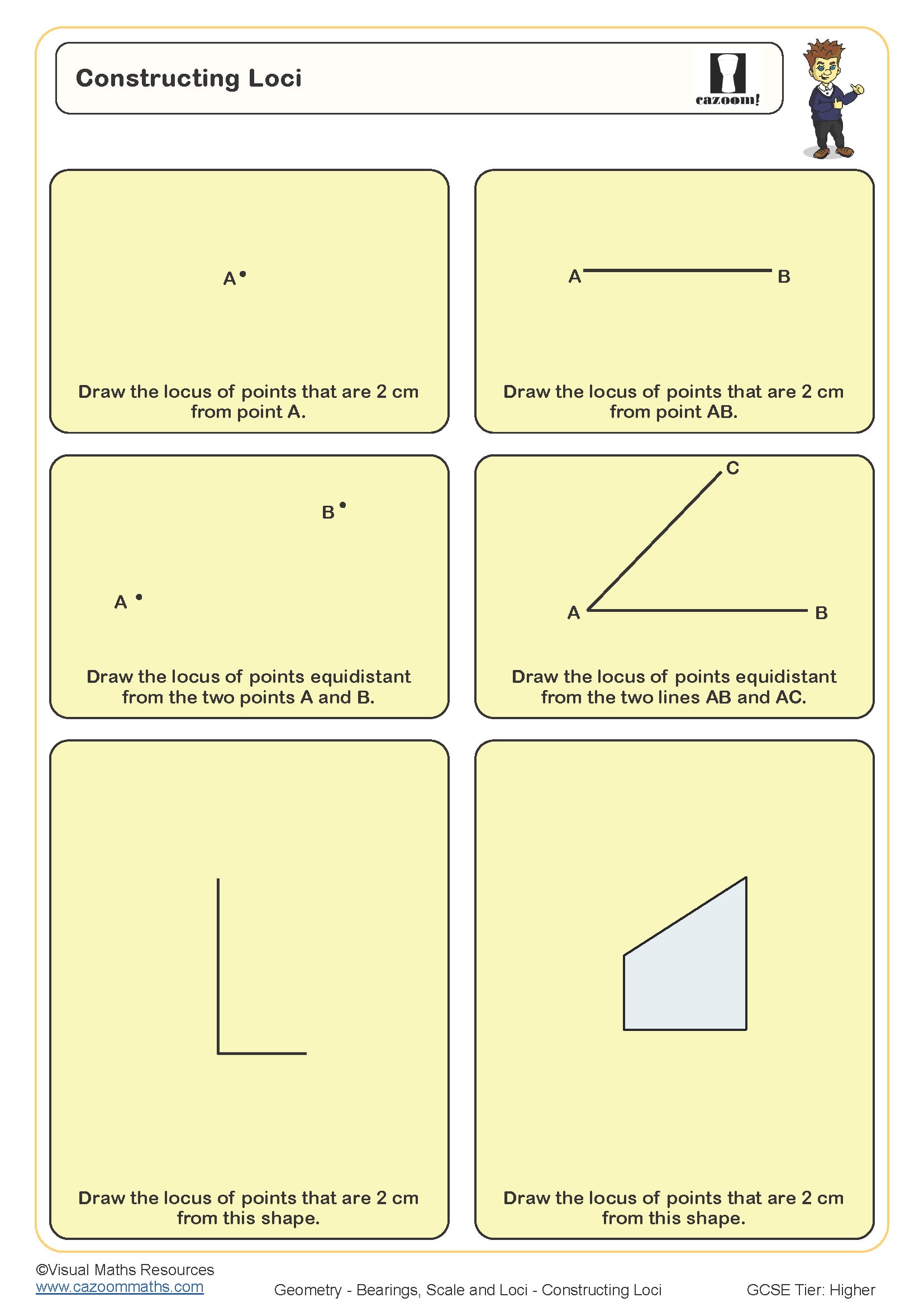
Constructions appear throughout Years 7, 8, and 9, with the complexity increasing as students progress through Key Stage 3. Year 7 typically introduces basic constructions like perpendicular and angle bisectors, establishing the fundamental compass techniques. Year 8 extends this to constructing triangles from given side lengths and angles, whilst Year 9 incorporates constructions into loci problems and inscribed shapes.
The progression centres on combining multiple construction techniques within single problems. Where Year 7 students might bisect a single angle, Year 9 students tackle questions requiring several constructions to locate specific points, such as finding the centre of a circle by constructing perpendicular bisectors of two chords. This layering of skills explains why early accuracy matters significantly for later success.
How Do Inscribed Shapes Connect to Constructions?
Inscribed shapes are polygons drawn inside circles with every vertex touching the circumference, and constructing them accurately requires understanding both angle properties and precise compass work. To inscribe a regular hexagon, students use the fact that the radius equals the side length, stepping the compass around the circle six times. For inscribed squares or triangles, perpendicular bisectors and angle properties combine with construction techniques.
Architects and engineers use inscribed constructions when designing circular features like rose windows in cathedrals or dividing circular components into equal segments for gears and rotors. These real-world applications require the same precision students practise with compass and ruler—CAD software essentially automates the geometric principles students learn through manual constructions, making this foundational knowledge relevant for modern technical design work.
How Can These Worksheets Support Construction Skills?
The worksheets provide structured practice that builds from single constructions to multi-step problems, allowing students to develop accuracy gradually. Questions are sequenced so students master one technique before combining it with others, and the answer sheets show all construction arcs and lines that should remain visible, helping students check their method as well as their final answer.
Many teachers use these resources for paired work where one student constructs whilst the other checks against the method sheet, developing peer assessment skills. They work effectively as intervention materials for students who struggle with geometric reasoning, as the physical act of constructing reinforces spatial understanding better than observing demonstrations alone. For homework, constructions require minimal equipment and give immediate visual feedback about accuracy, helping students self-correct before the next lesson.