KS3 Function Machines Worksheets
What are function machines in KS3 maths?
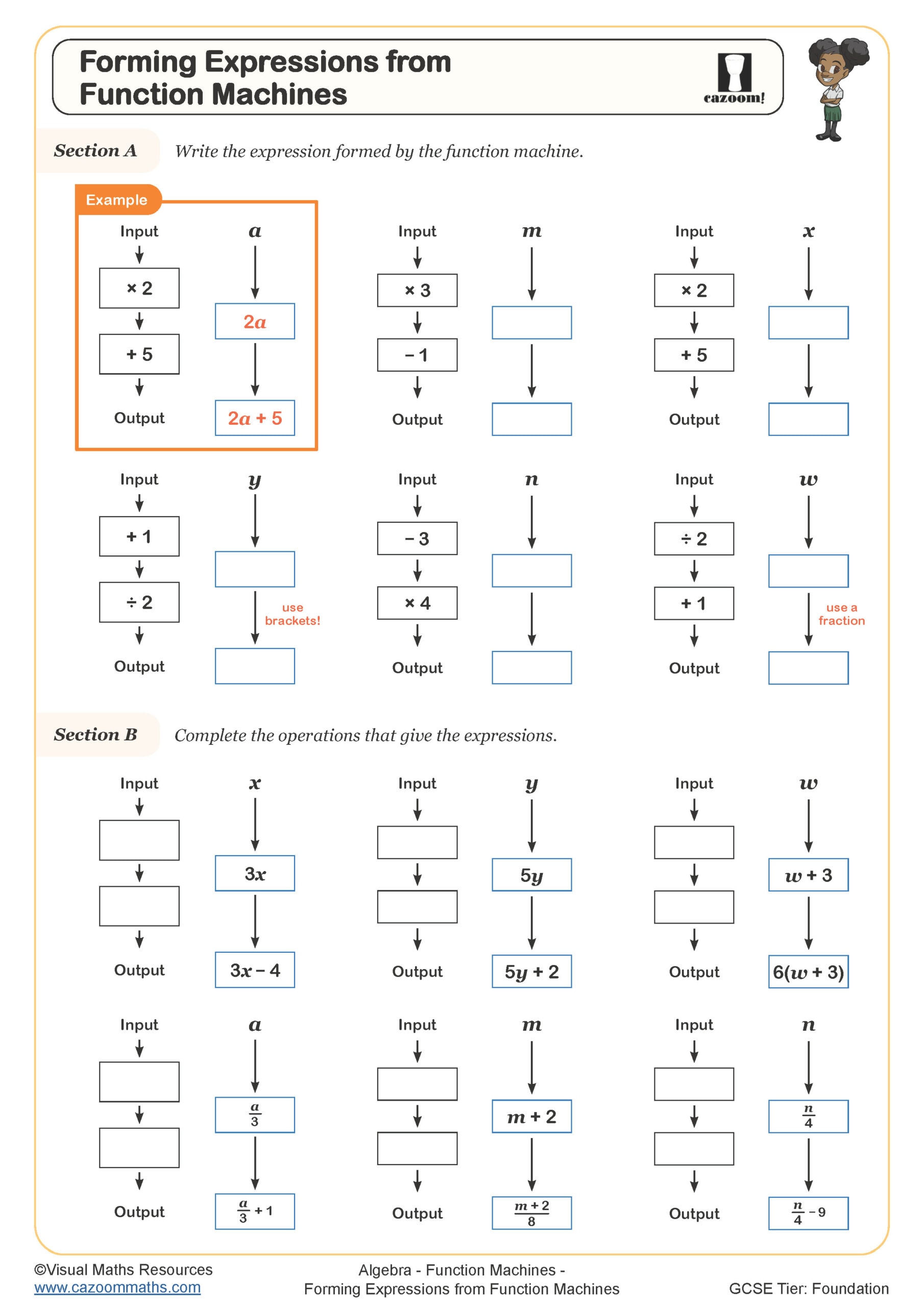
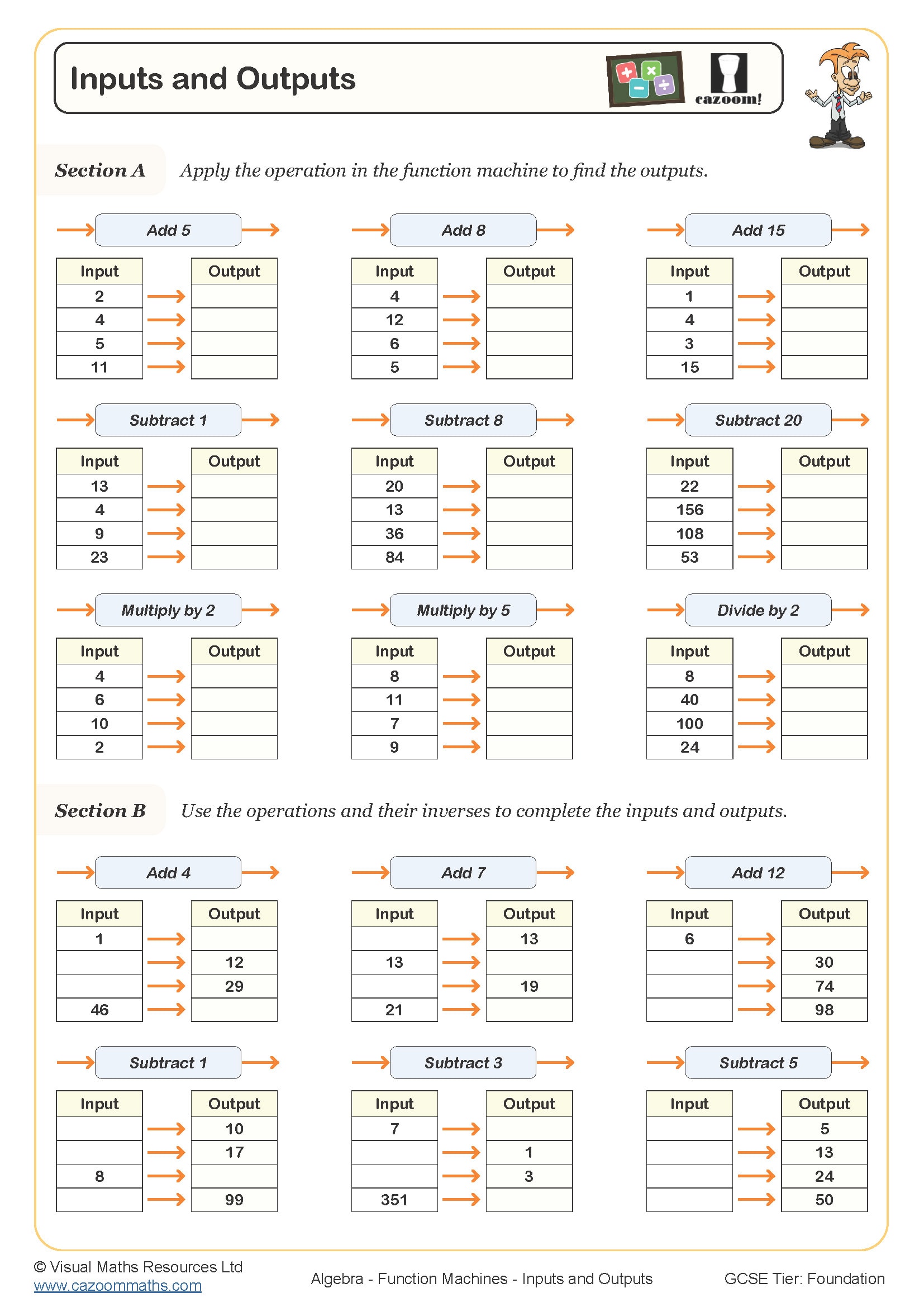
Function machines are visual representations that show how an input value is transformed through one or more operations to produce an output. At KS3, students encounter these as diagrams with boxes or arrows showing operations like 'multiply by 3' or 'subtract 5', building foundational understanding of functions before formal algebraic notation arrives later in the curriculum. The machines help students grasp that functions are consistent rules applied to any input.
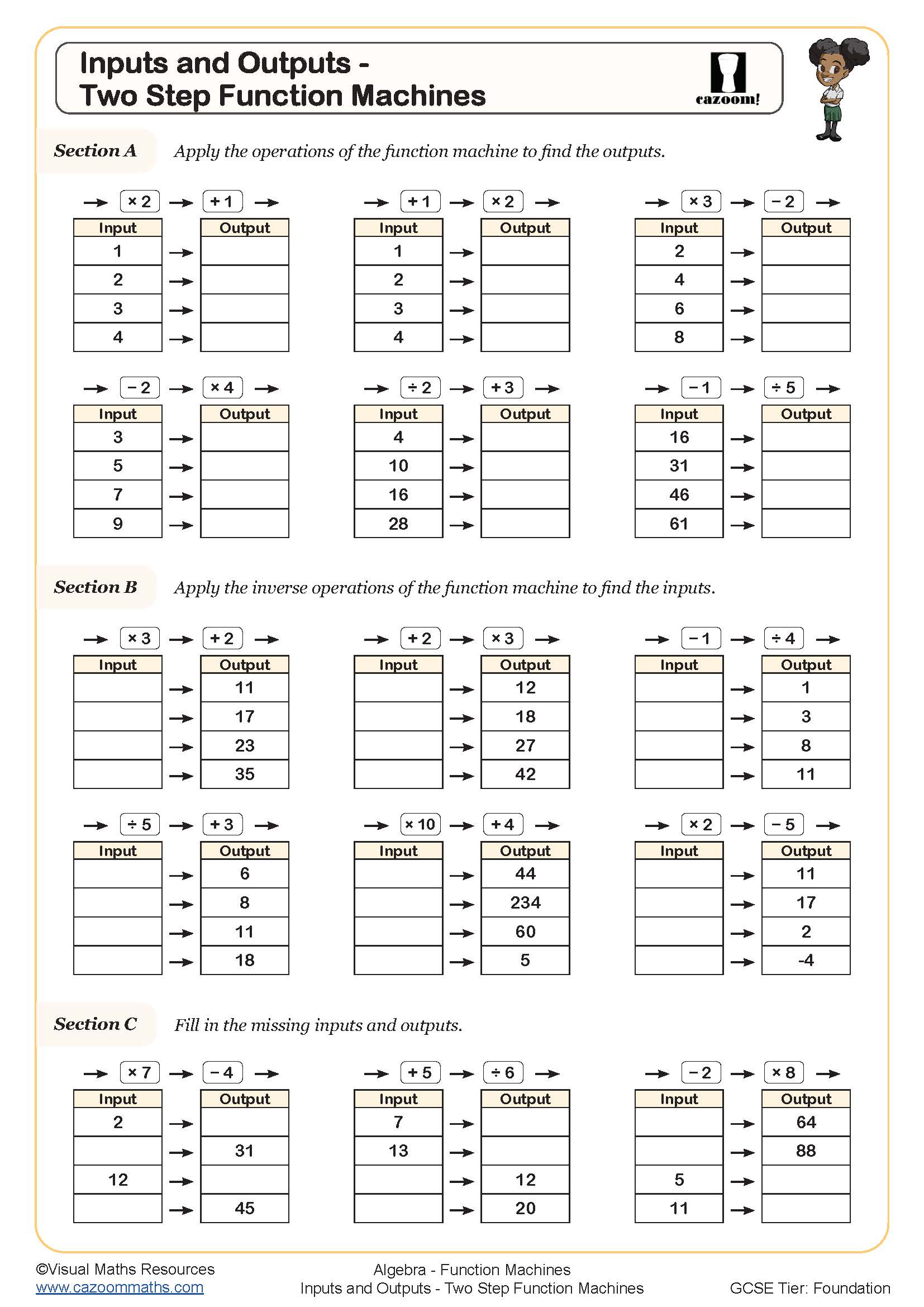
A common error occurs when students work with two step function machines and reverse the order of operations when finding inverse functions. For example, if the machine shows '×4 then +7', students often incorrectly reverse it as '×4 then -7' rather than '-7 then ÷4'. This highlights why systematic practice with both forward and backward processes matters before algebraic manipulation begins in earnest.
Which year groups study function machines?
These worksheets suit Year 7, Year 8, and Year 9 students working through the KS3 programme of study. Function machines typically appear in Year 7 as an introduction to algebraic thinking, forming a bridge between arithmetic operations and formal algebra. The National Curriculum expects students to understand functions and express them using algebra, with function machines providing concrete visual scaffolding for this abstract concept.
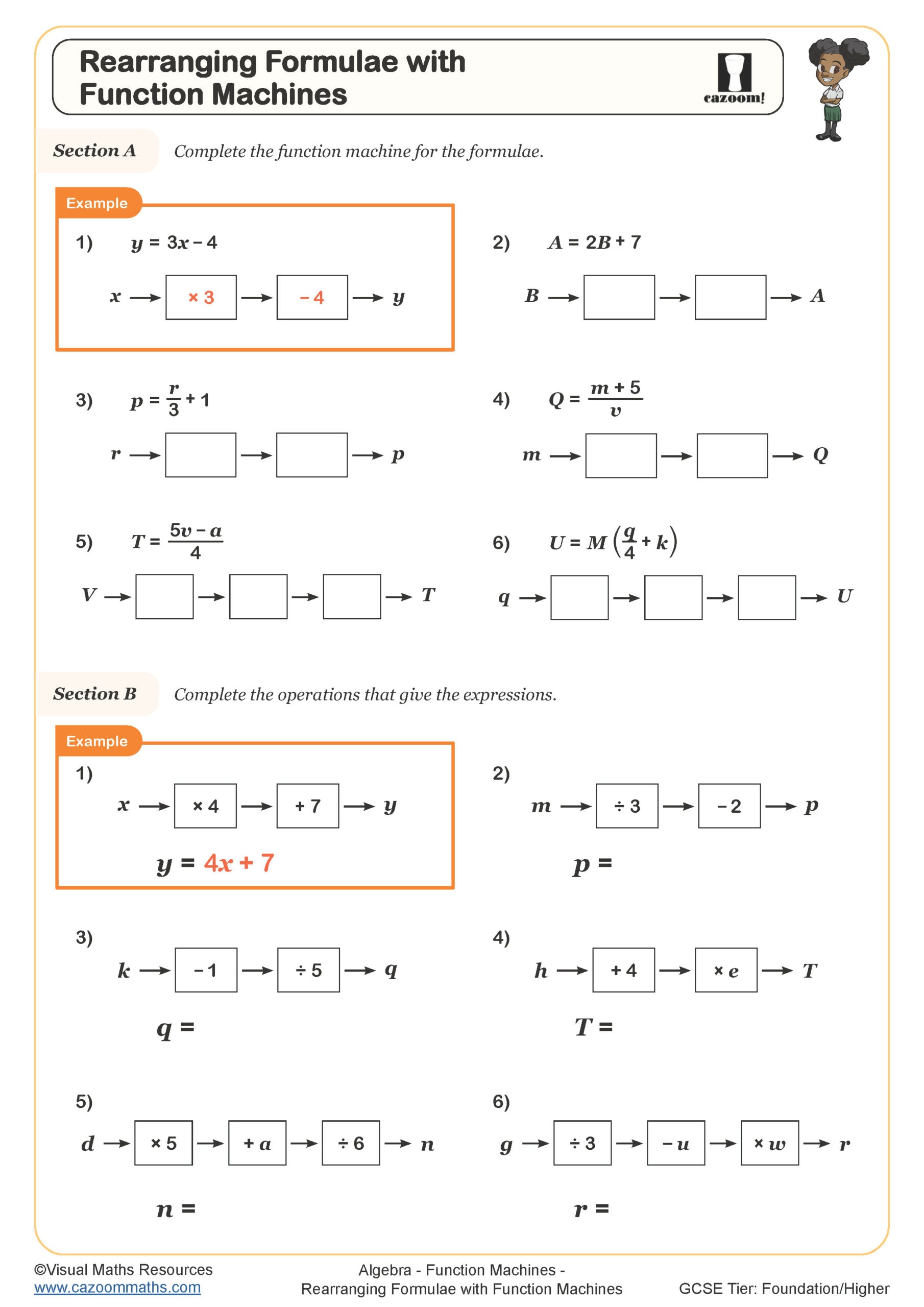
Progression across KS3 becomes more sophisticated: Year 7 students generally work with single-step machines and simple two-step operations, Year 8 extends to more complex combinations including negative numbers and decimals, whilst Year 9 students encounter function notation like f(x) and may reverse multi-step processes algebraically. This gradual increase in complexity ensures students build confidence before tackling composite and inverse functions at GCSE.
How do two step function machines prepare students for algebra?
Two step function machines require students to apply operations sequentially, mirroring the order of operations they'll use throughout algebra. When a student sees 'input → ×3 → +5 → output', they're building the mental framework for expressions like 3x + 5. This visual approach helps students understand that mathematical operations happen in a specific sequence and that reversing processes requires careful logical thinking about inverse operations.
This skill connects directly to programming and computational thinking, where functions transform inputs to outputs through defined algorithms. Software engineers and data scientists use function notation constantly, whether filtering datasets or defining user interfaces. Manufacturing processes also rely on sequential operations where one step's output becomes the next step's input, from production lines to quality control systems. Understanding how operations combine and reverse underpins both mathematical problem-solving and practical STEM applications.
How can teachers use these function machine worksheets effectively?
The worksheets provide structured practice that progresses from identifying outputs when given inputs and operations, through to determining unknown operations or inputs. Answer sheets allow students to self-check during independent work, whilst the visual format makes function machines particularly effective for paired activities where one student calls out an input and their partner calculates the output. This immediate feedback helps identify misconceptions before they become embedded.
Many teachers use these worksheets during starter activities to reinforce mental arithmetic alongside algebraic thinking, or as targeted intervention for students who struggle with inverse operations. They work well as homework because the visual structure helps parents support their children without needing deep mathematical knowledge. The progression from simple to complex across different worksheets also makes them valuable for differentiation, allowing teachers to match challenge level to individual student needs within mixed-ability classes.