KS3 Number Lines Worksheets
What are number line sheets used for in KS3 maths?
Number line sheets are visual representations that help students understand number order, scale, and the relationships between values. In KS3, they're particularly valuable for reinforcing place value with decimals, comparing negative numbers, and modelling arithmetic operations. These worksheets bridge the concrete understanding developed in primary school with the more abstract algebraic thinking required at GCSE.
Teachers often notice that students who struggle with mental arithmetic benefit significantly from number line practice, as it provides a visual scaffold for calculation. A common error occurs when students count the marks rather than the intervals between them, leading to off-by-one mistakes. Exam questions increasingly expect students to use number lines independently for estimation and checking, making this a skill worth developing systematically through Years 7 and 8.
Which year groups use number line worksheets at KS3?
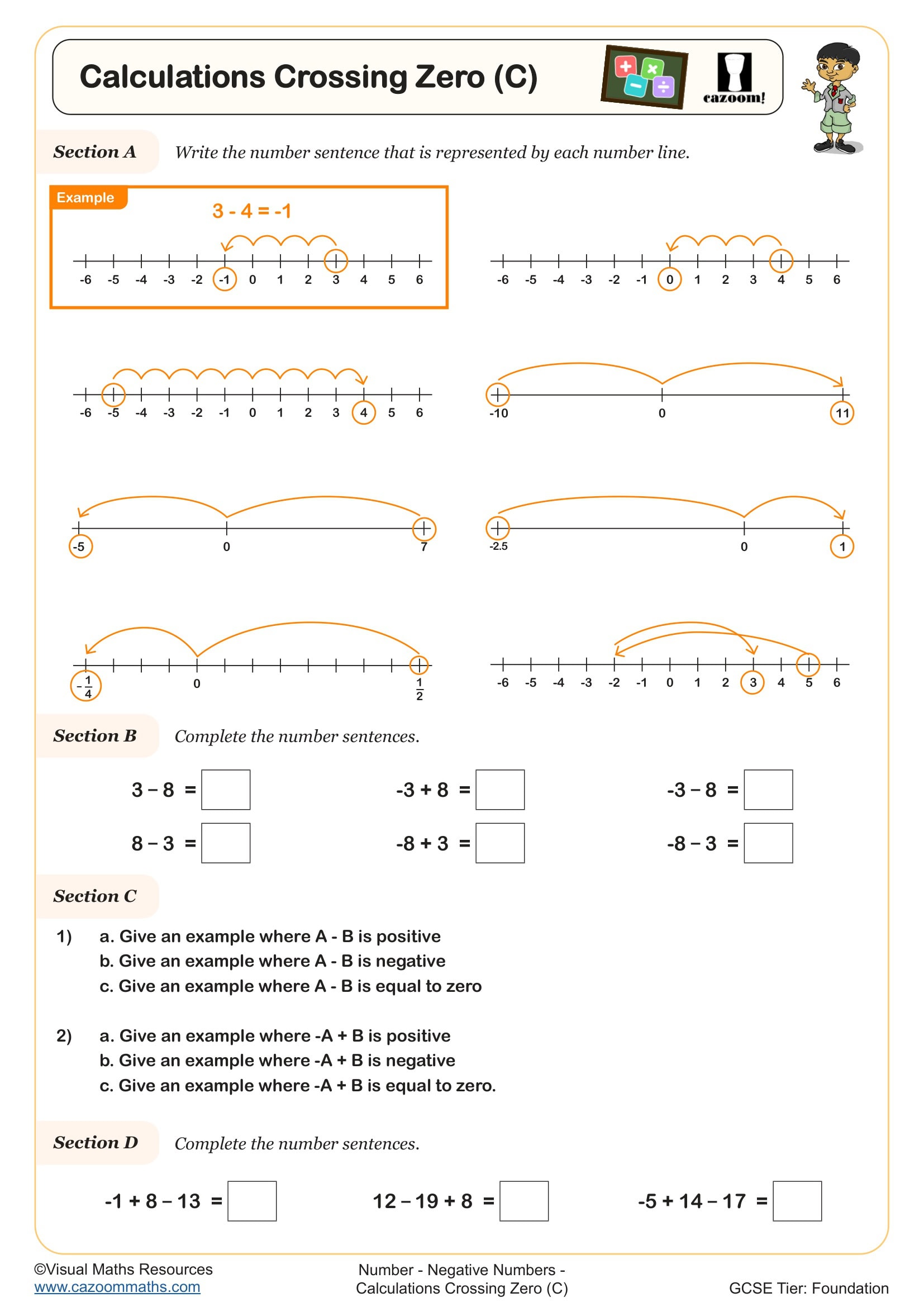
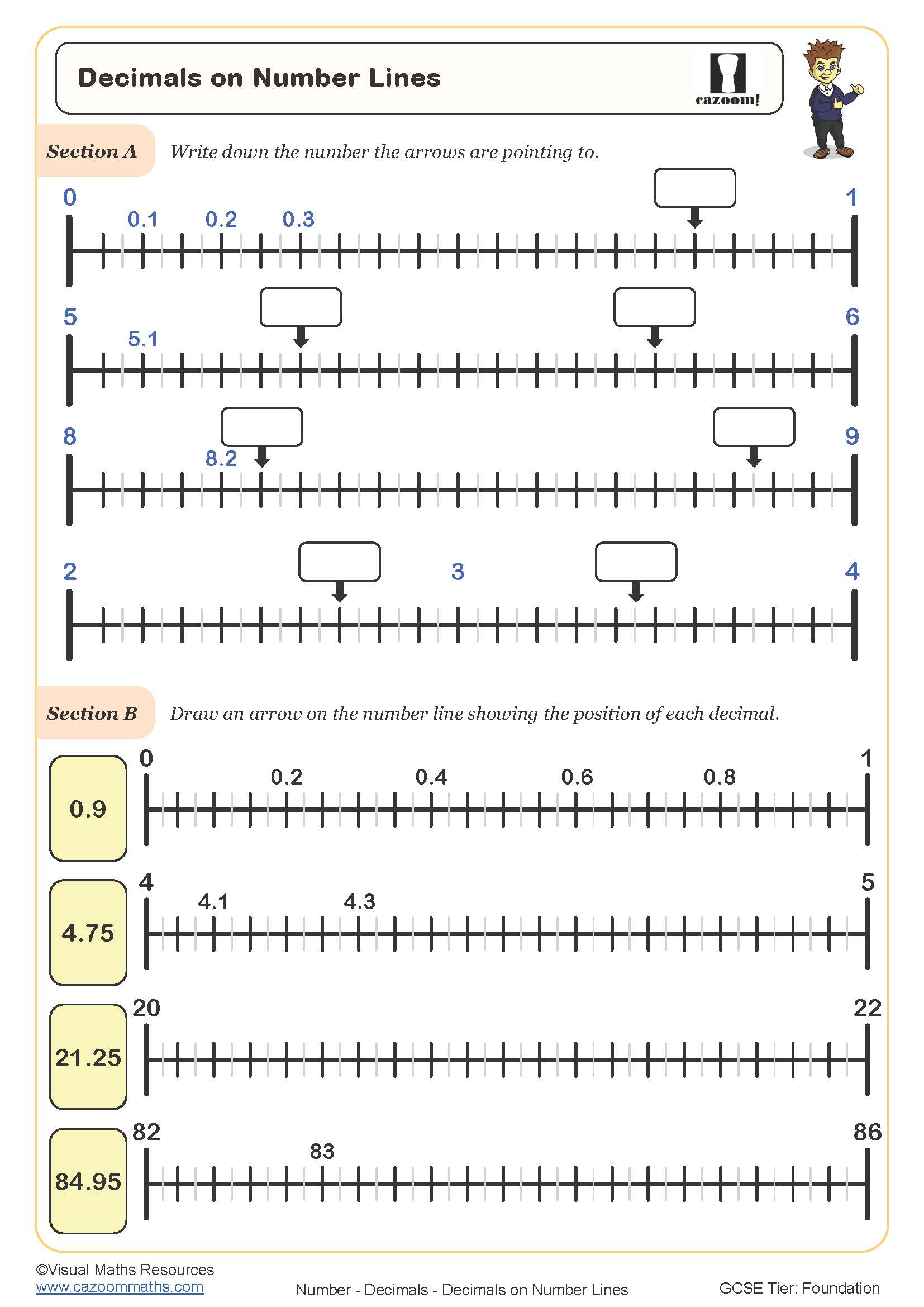
These worksheets are designed for Year 7 and Year 8 students following the National Curriculum for England. In Year 7, number lines typically reinforce understanding of integers, simple decimals, and ordering numbers, building on primary skills. Students also use them to visualise addition and subtraction, particularly when working across zero with negative numbers.
By Year 8, the focus shifts to more complex applications: subtracting decimals with different numbers of decimal places, working with exchanges between units, and using number lines as problem-solving tools for multi-step questions. The progression reflects increasing confidence with scale and precision, preparing students for coordinate geometry and inequalities work in Year 9. Teachers find that revisiting number lines at different difficulty levels helps address gaps for students who've developed procedural methods without conceptual understanding.
How do number lines help with subtracting decimals?
Subtracting decimals using number lines makes the process visual and reduces the procedural errors common with column methods. Students place the larger number on the line, then count backwards or find the difference by 'jumping' to the smaller number, keeping track of the intervals. This approach particularly helps when decimals have different numbers of digits, as the number line naturally shows equivalent positions without requiring students to 'add zeros'.
This skill has direct applications in measurement and data contexts throughout STEM subjects. Scientists use number line reasoning when reading scales on instruments, calculating differences between readings, or estimating experimental error. In Design and Technology, students subtract decimal measurements when calculating tolerances or material requirements. Making these connections explicit helps students understand why precision with decimal subtraction matters beyond the maths classroom, particularly when a tenth of a millimetre might determine whether components fit together properly.
How can teachers use these number line worksheets effectively?
The worksheets build from simpler tasks like marking positions on pre-drawn number lines to more demanding skills such as choosing appropriate scales or using number lines to solve word problems. This scaffolding allows teachers to match tasks to individual student needs, making them particularly useful for mixed-attainment classes. The included answer sheets support independent practice and enable students to self-check, developing metacognitive skills alongside mathematical understanding.
Many teachers use number line worksheet pdf resources for targeted intervention with students who rely too heavily on calculator methods without understanding. They're also effective as homework tasks because parents can easily follow the visual method, unlike some abstract algorithms. In paired work, asking one student to explain their number line reasoning to another often reveals misunderstandings about scale or direction. The worksheets work well as retrieval practice starters, particularly when revisiting decimal work before introducing similar concepts with fractions or percentages.