KS3 Powers Worksheets
Add and Subtract in Standard Form

Calculating Using Standard Form

Calculations Using Indices (A)
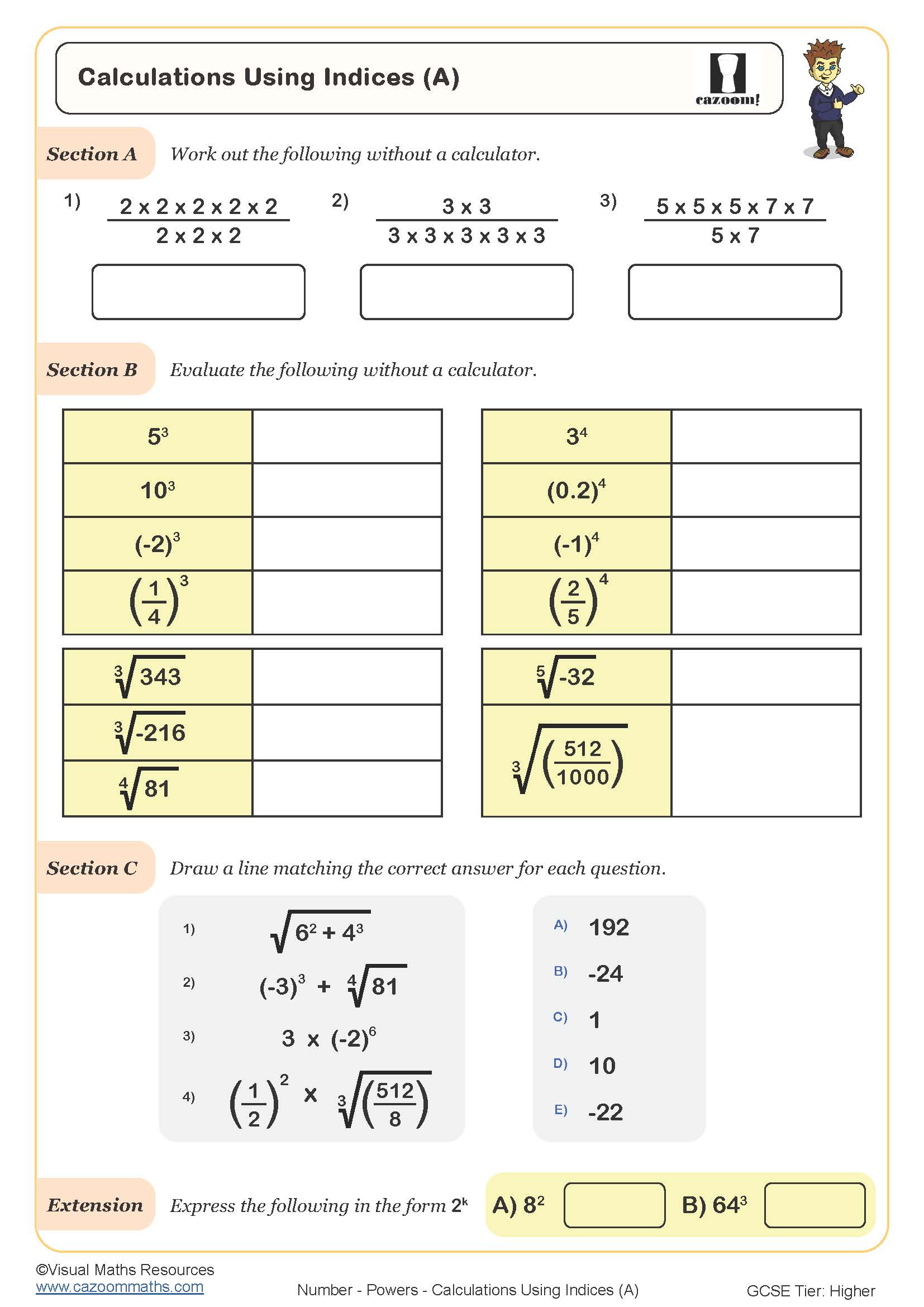
Calculations Using Indices (B)

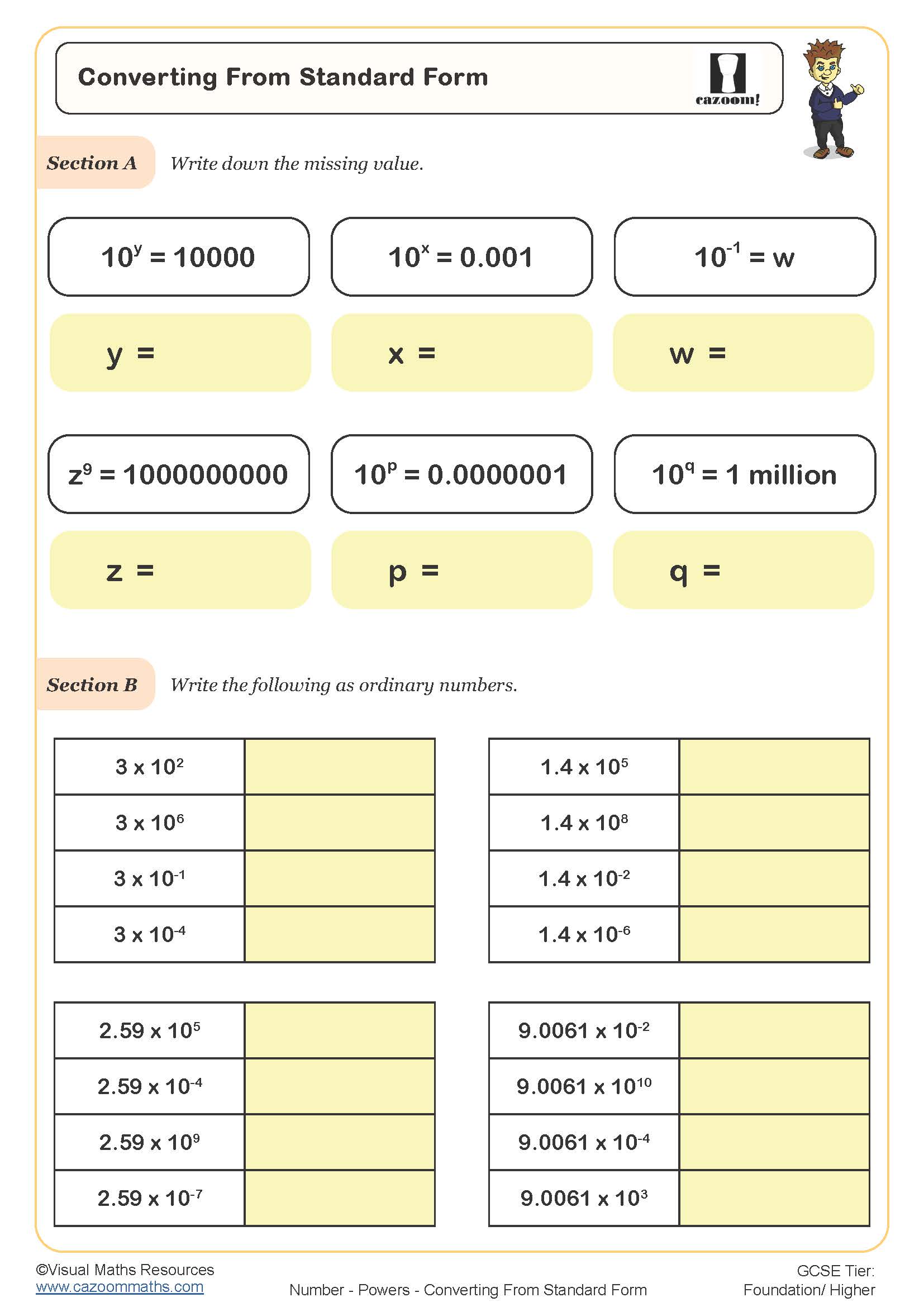
Converting from Standard Form
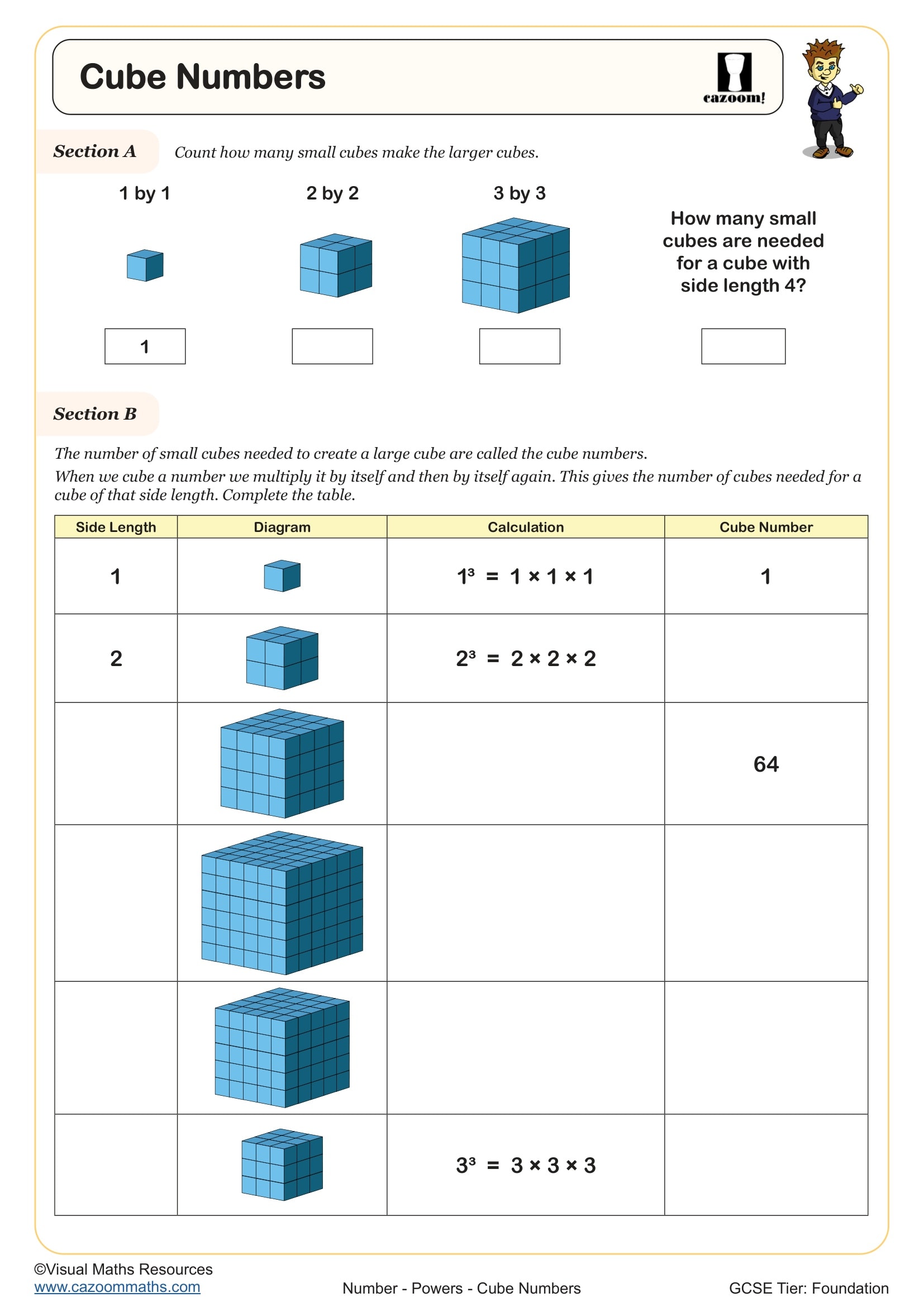
Cube Numbers
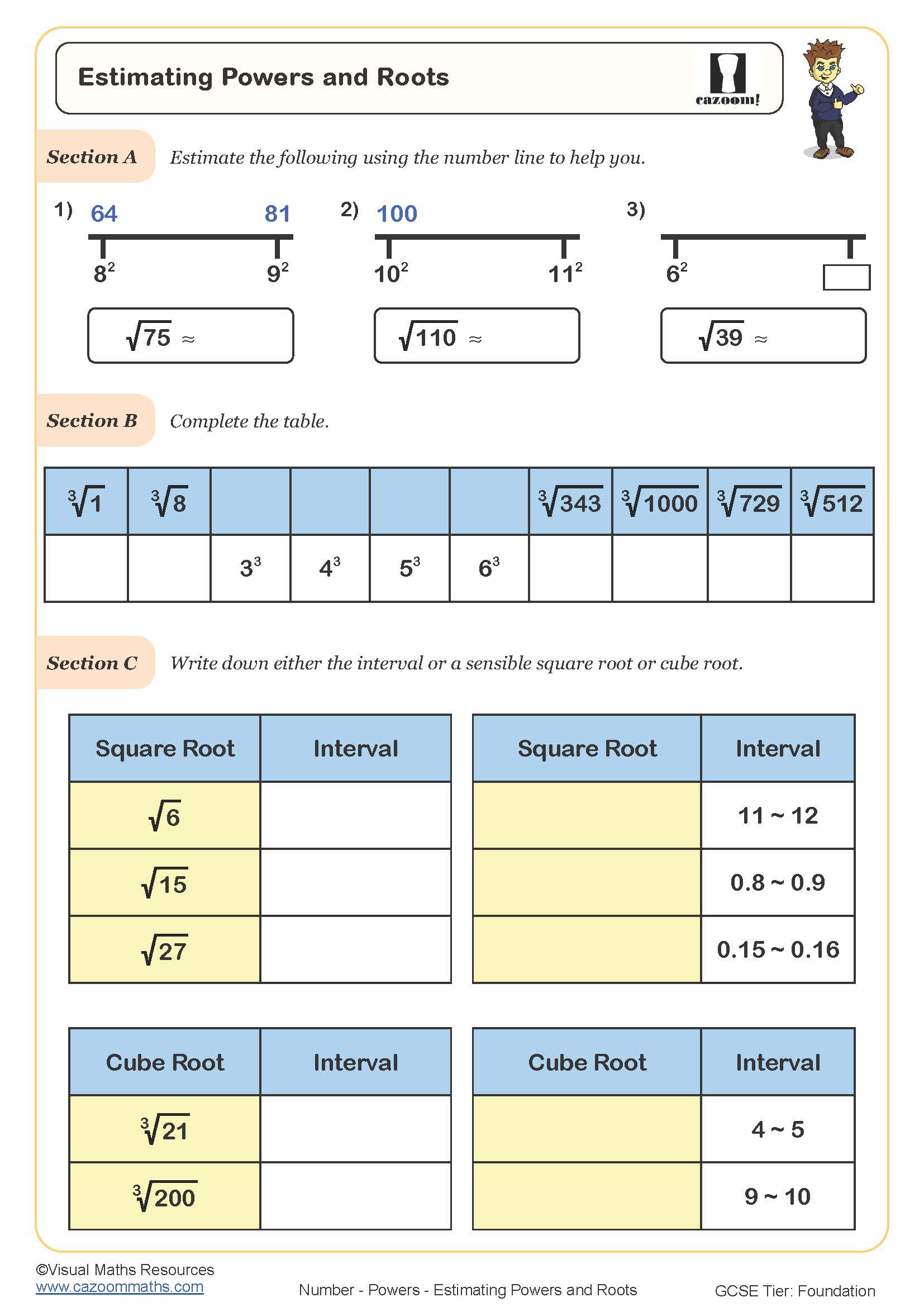
Estimating Powers and Roots
Estimating Square Roots

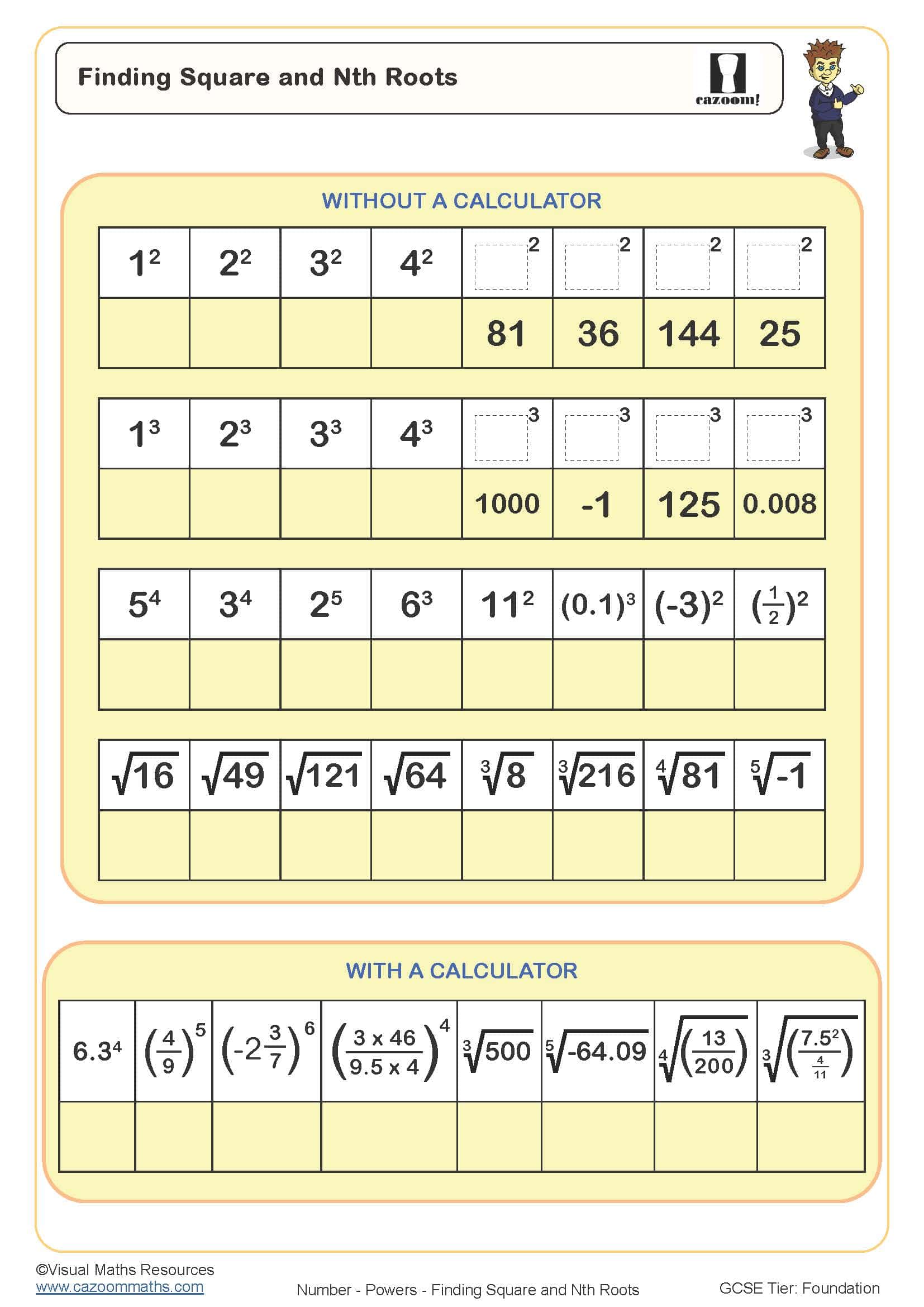
Finding Square and Nth Roots
Manipulating Standard Form (A)

Manipulating Standard Form (B)

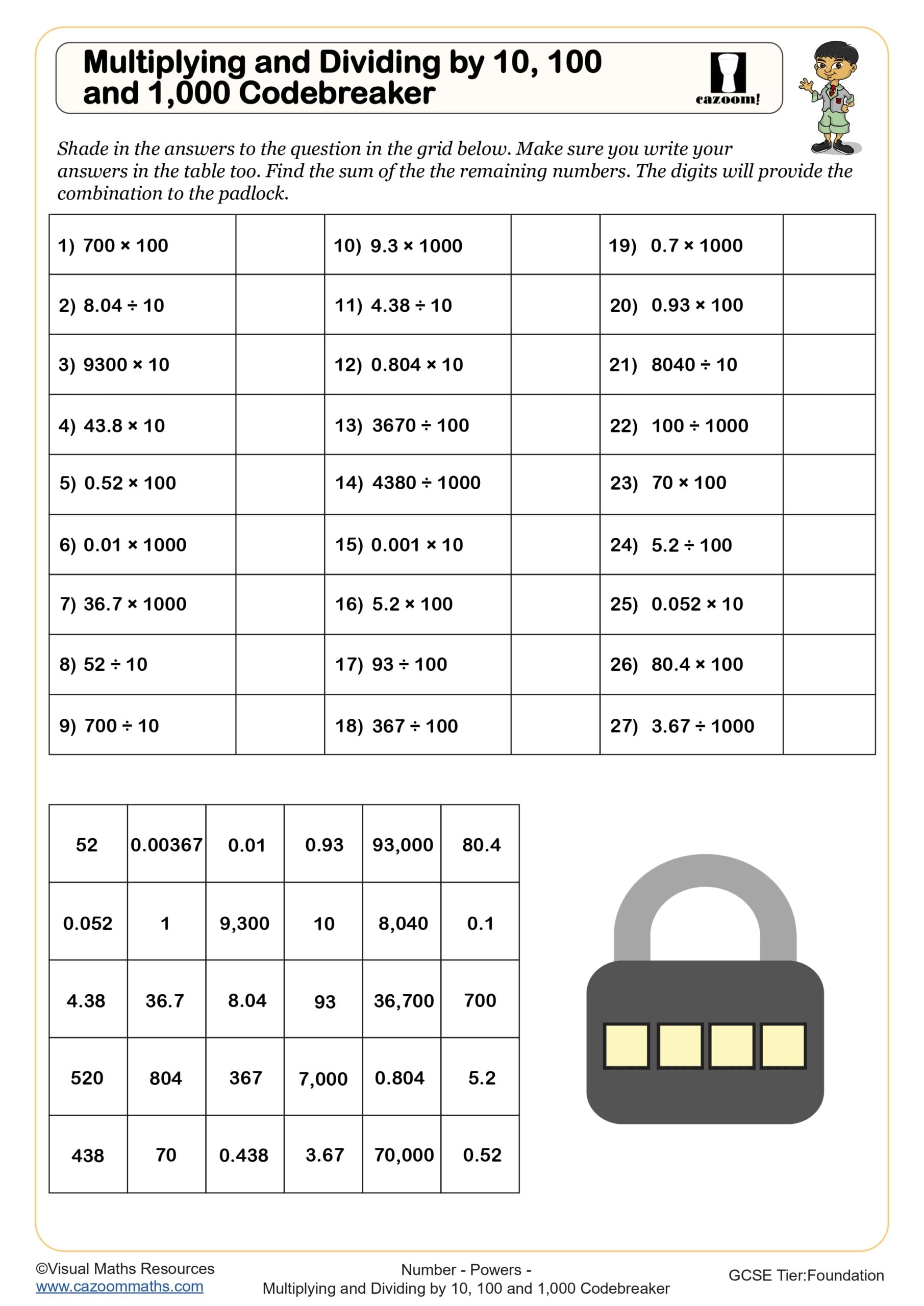
Multiplying and Dividing by 10, 100 and 1,000 Codebreaker
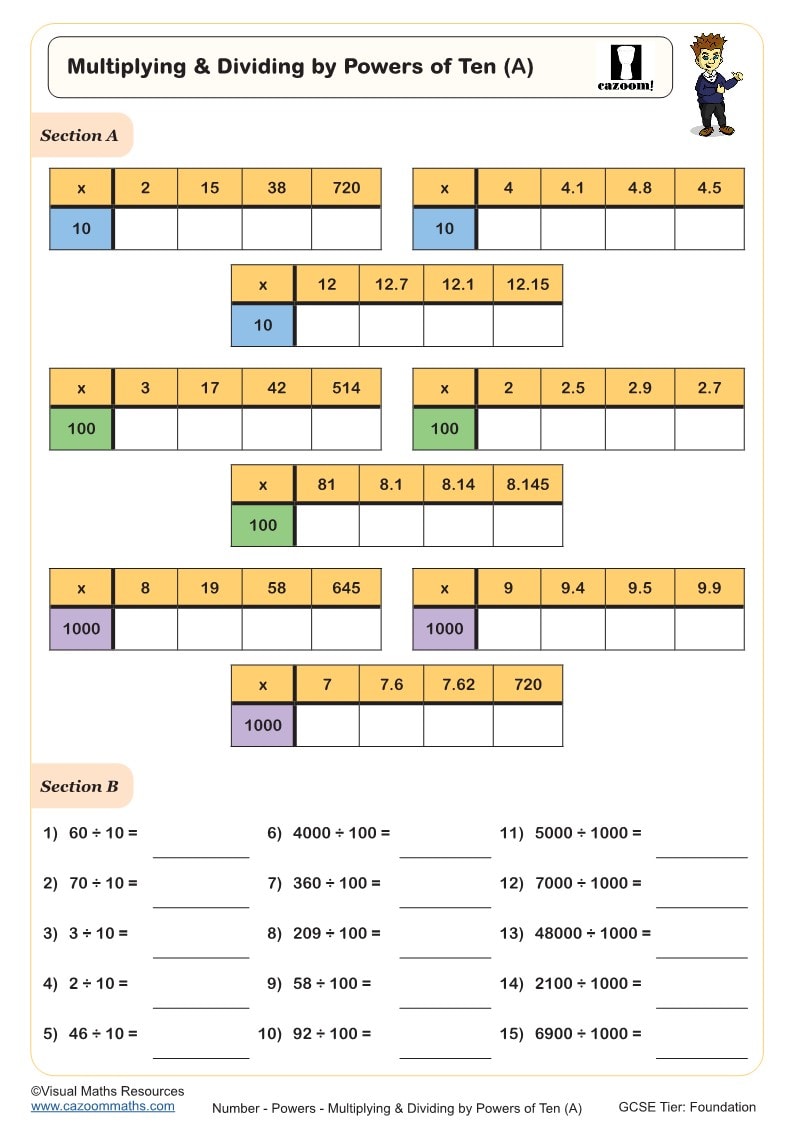
Multiplying and Dividing by Powers of Ten (A)
Multiplying and Dividing by Powers of Ten (B)

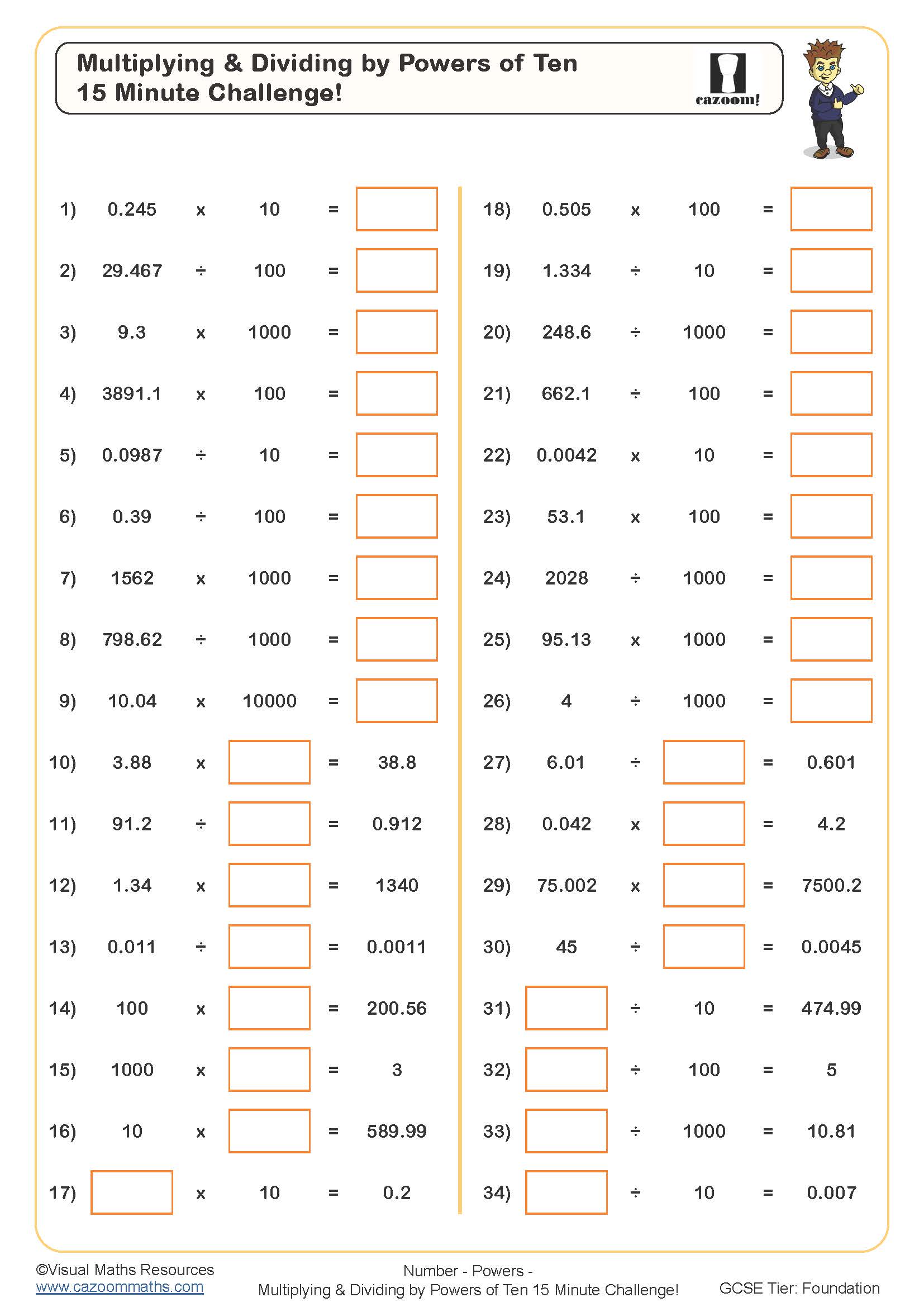
Multiplying and Dividing by Powers of Ten 15 Minute Challenge
Multiplying and Dividing by Ten

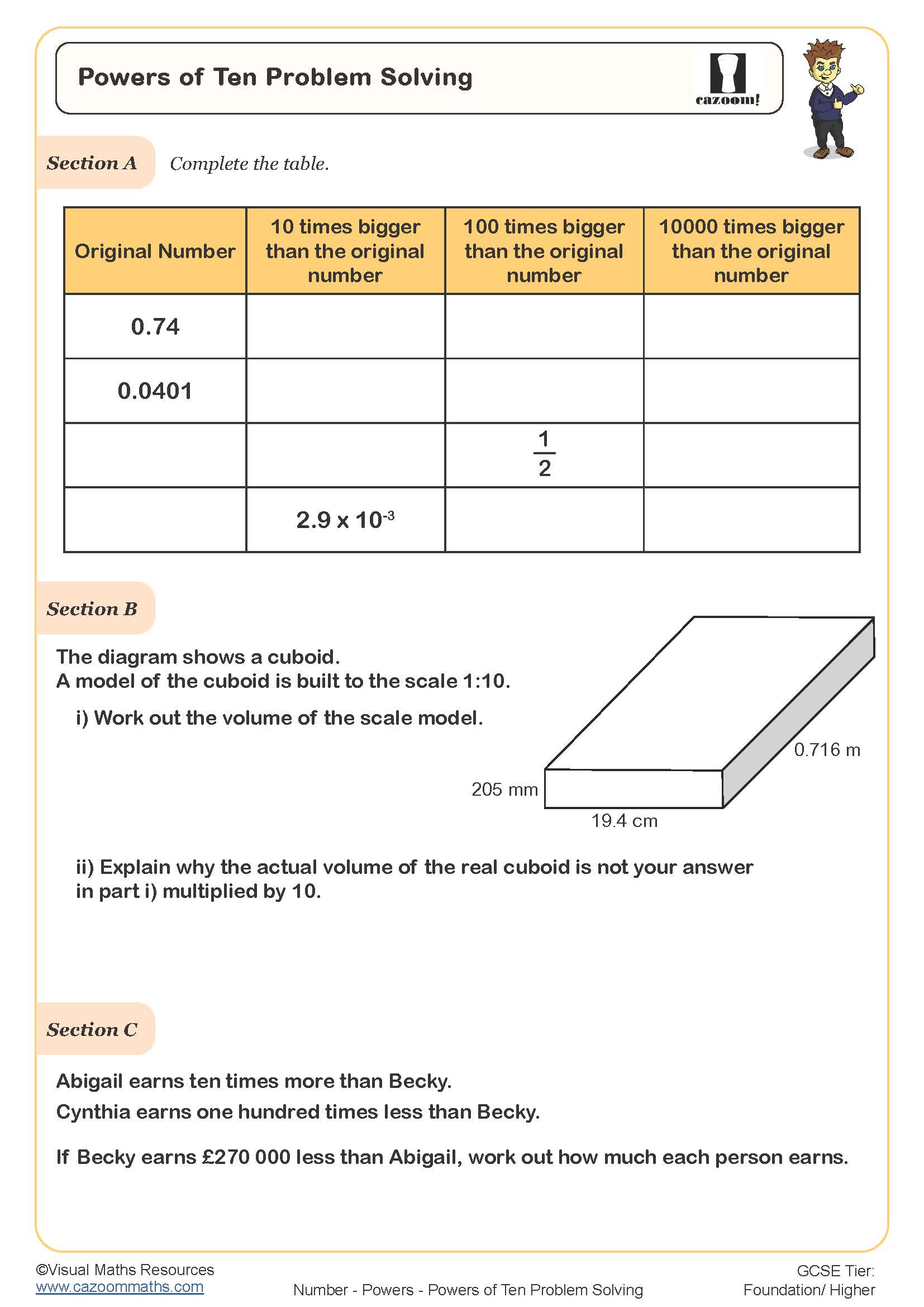
Powers of Ten Problem Solving
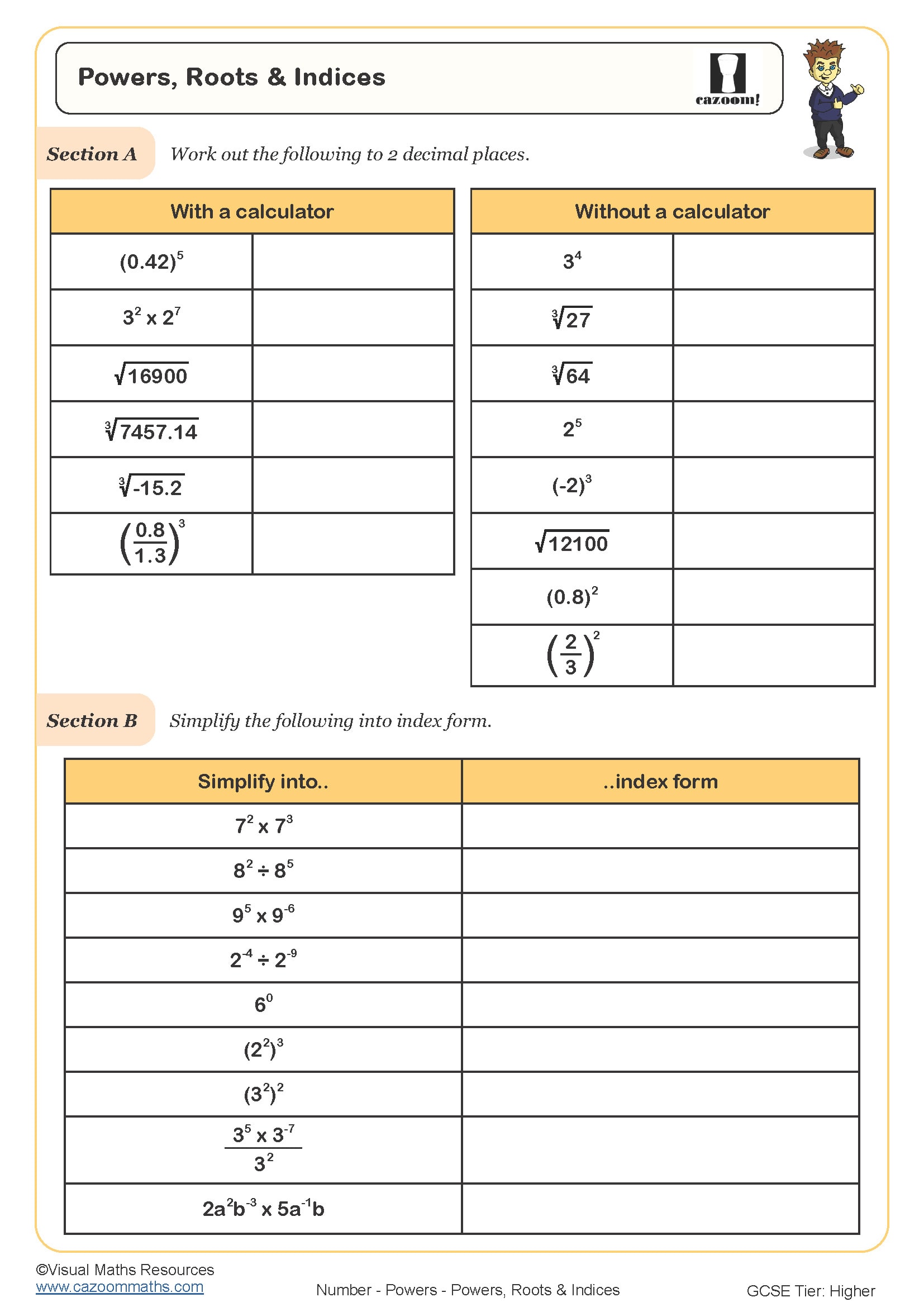
Powers, Roots and Indices
Recognising Standard Form

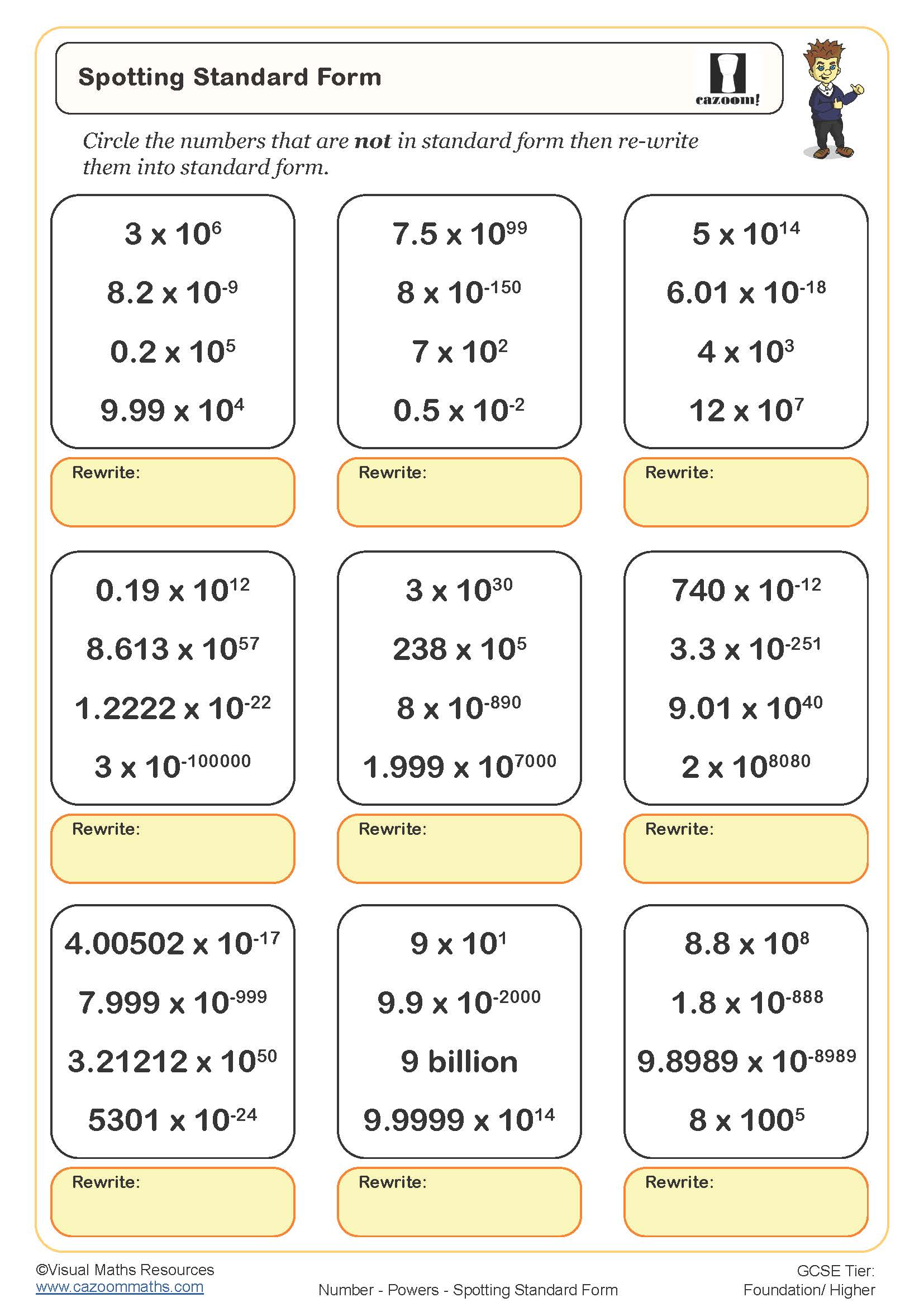
Spotting Standard Form
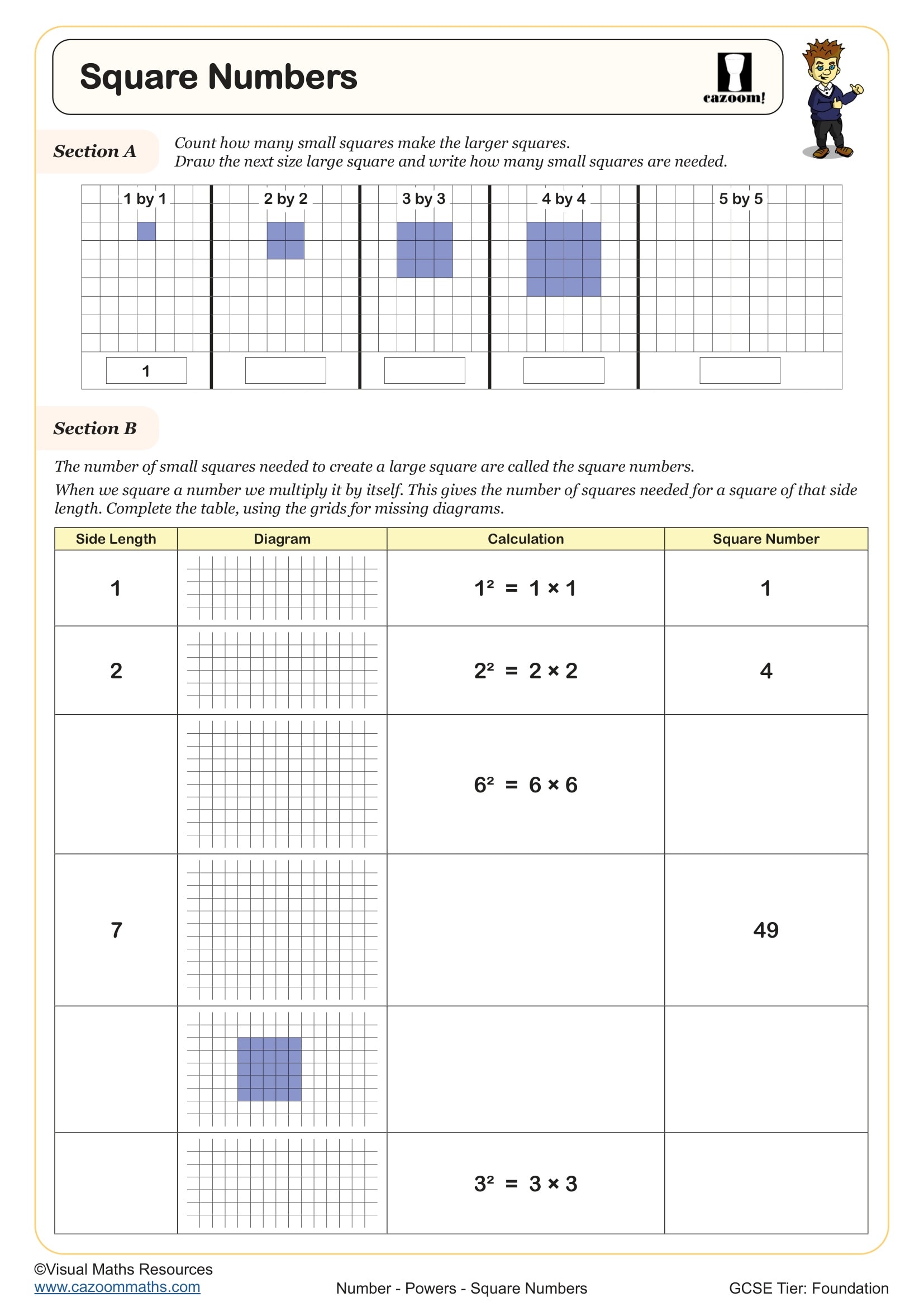
Square Numbers
Square Numbers, Cube Numbers and Other Powers

Standard Form (A)
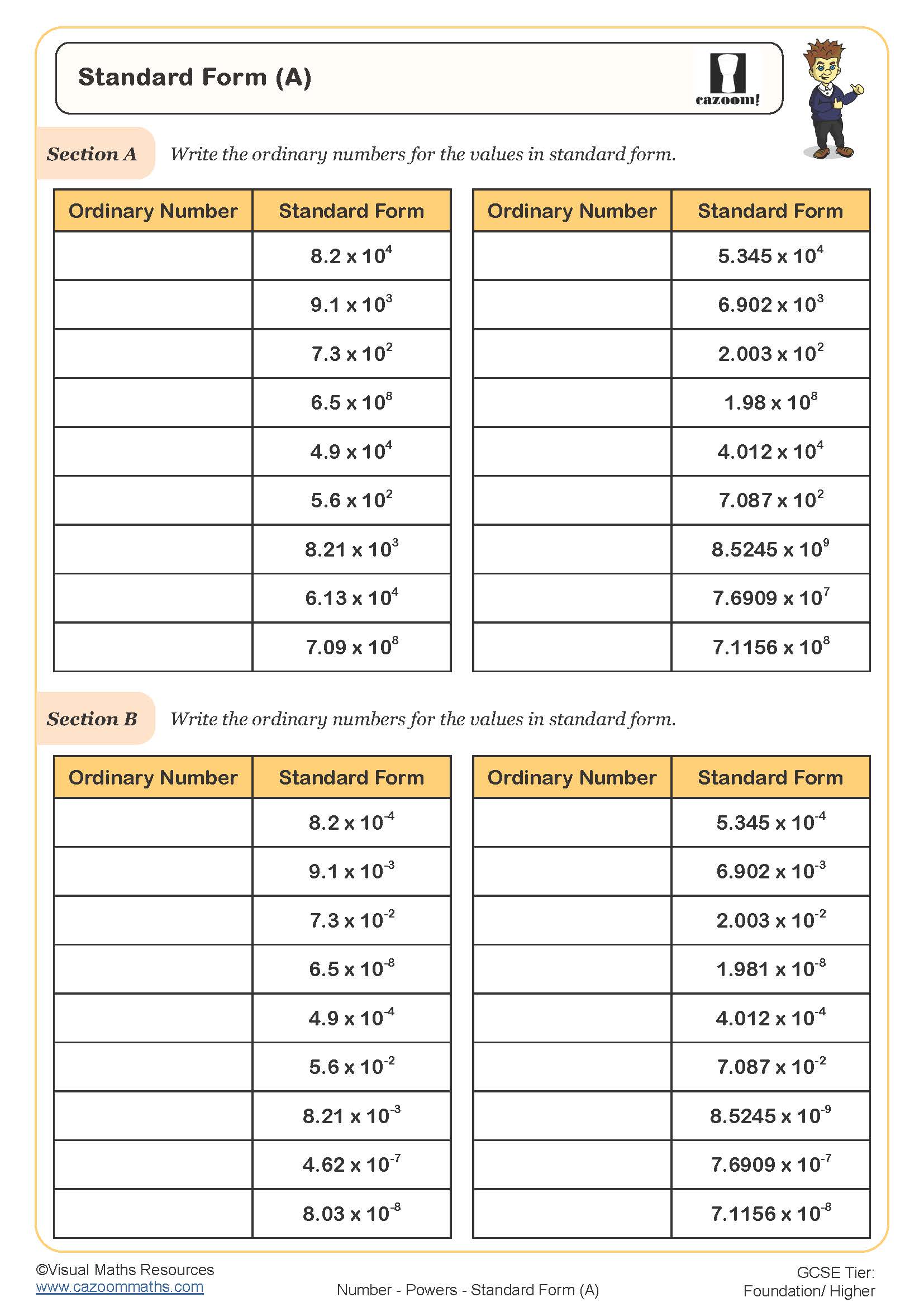
Standard Form (B)
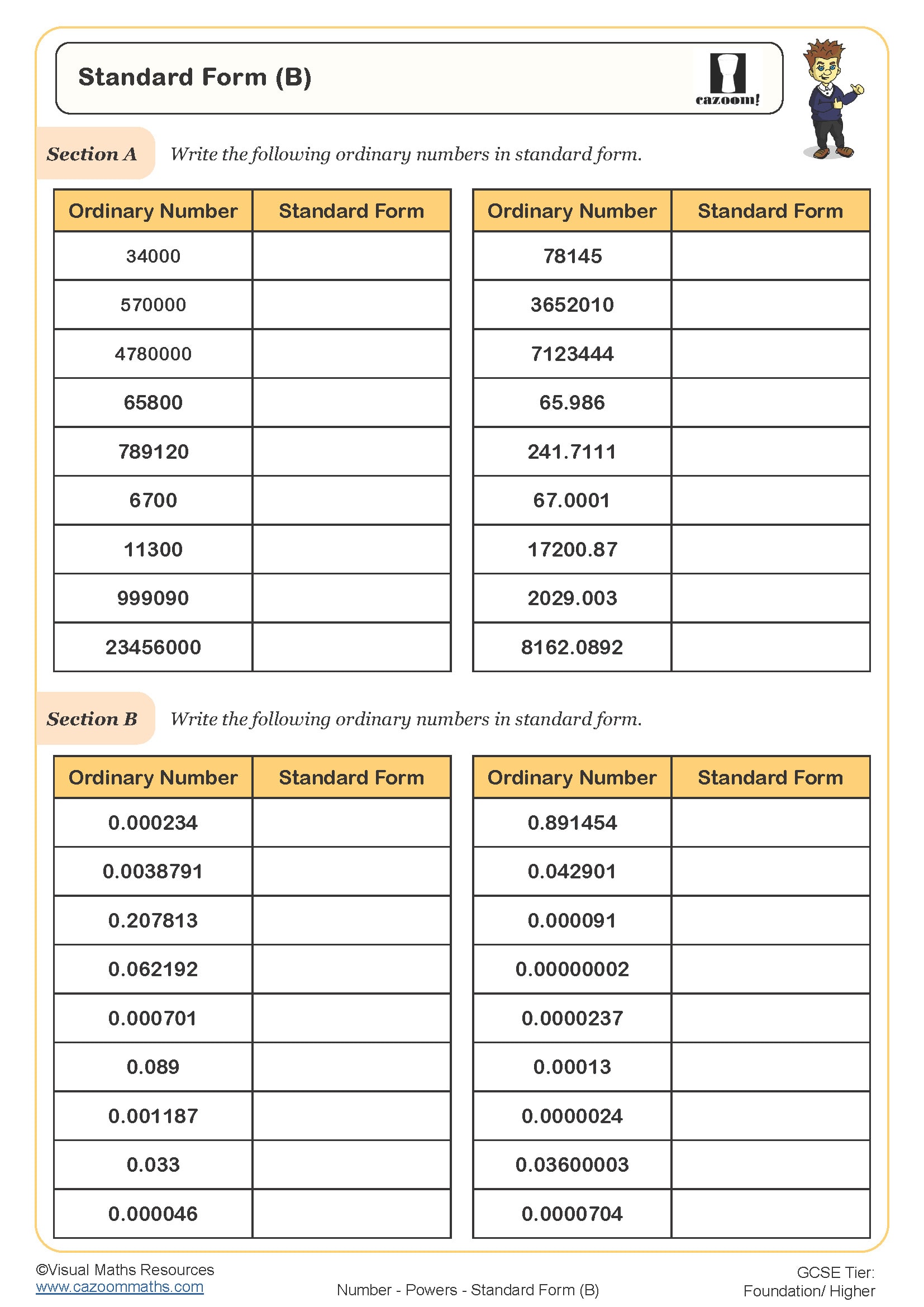
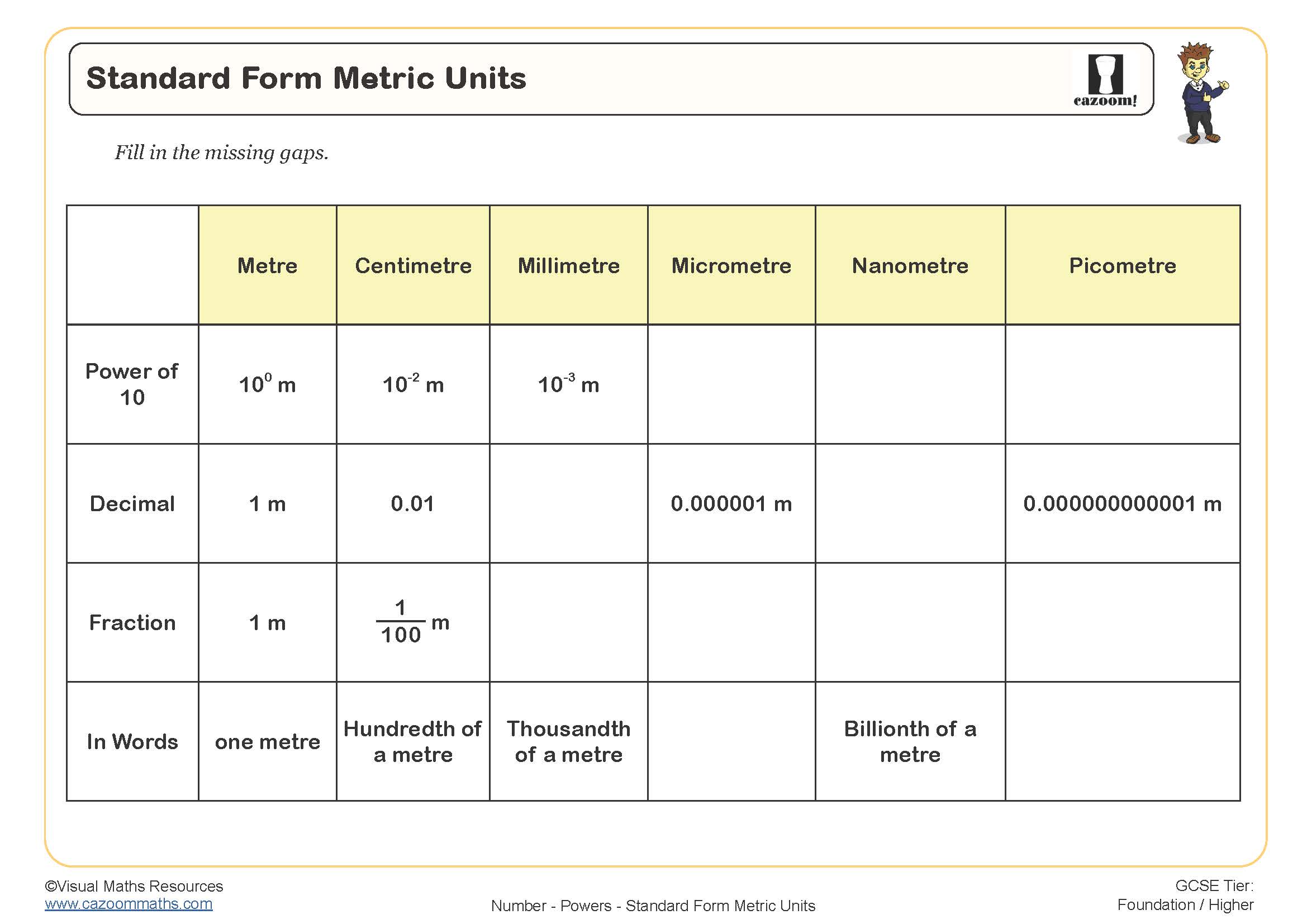
Standard Form Metric Units
Standard Form Problem Solving

What are the laws of indices and why do students struggle with them?
The laws of indices are rules for working with powers: when multiplying powers with the same base, add the indices (a^m × a^n = a^(m+n)); when dividing, subtract them (a^m ÷ a^n = a^(m-n)); and when raising a power to another power, multiply the indices ((a^m)^n = a^(mn)). Students first encounter these rules in Year 7 and build on them throughout KS3, with the laws forming essential foundations for algebra and equations.
A persistent mistake occurs when students see 2³ × 2⁴ and write 4⁷ instead of 2⁷, multiplying the bases rather than keeping the base constant. This stems from confusing index laws with standard multiplication. Exam mark schemes regularly penalise this error, particularly in multi-step algebraic questions where the mistake compounds through the working.
Which year groups study powers at KS3?
Powers appear across Year 7, Year 8, and Year 9 at KS3, with each year building on previous understanding. Year 7 students start with positive integer powers, recognising index notation and calculating values like 5³. Year 8 introduces the laws of indices for multiplication and division, alongside zero and negative powers. Year 9 extends to fractional indices, connecting them to roots, and applying index laws in algebraic contexts.
The progression reflects how index notation underpins increasingly sophisticated maths. Students who grasp that 8^(1/3) means the cube root of 8 in Year 9 are better prepared for exponential functions and logarithms at GCSE. Teachers often find that revisiting the meaning of indices as repeated multiplication helps bridge understanding between arithmetic powers and algebraic applications.
How do fractional indices connect to roots?
Fractional indices represent roots: a^(1/n) means the nth root of a. So 16^(1/2) equals the square root of 16, which is 4, whilst 27^(1/3) equals the cube root of 27, giving 3. When the numerator isn't 1, as in a^(m/n), this means the nth root of a raised to the power m. Students learn this connection in Year 9, building on their work with square roots and cube roots from earlier years.
This notation appears throughout STEM fields, particularly in physics formulas. The intensity of sound decreases with distance following an inverse square law, expressible using negative fractional powers. In engineering, stress-strain relationships and scaling laws routinely use fractional indices to model how properties change. Understanding that these fractional powers aren't arbitrary symbols but represent concrete operations helps students see maths as a practical language for describing real phenomena.
How can teachers use these powers worksheets effectively?
The worksheets scaffold learning by grouping similar question types before mixing operations, allowing students to consolidate one index law before tackling combined problems. Questions progress from numerical examples to algebraic expressions, helping students recognise that the same rules apply whether working with 3⁴ or x⁴. Answer sheets enable students to self-check during independent work, encouraging them to identify where they've applied the wrong law and correct their approach.
Many teachers use these worksheets for targeted intervention when formative assessment reveals gaps in index understanding. The 15-minute worksheets work particularly well as starter activities to retrieve prior knowledge before introducing new content. For homework, the structured progression allows students to work independently whilst parents can support using the answers provided. Paired work activities where students explain their reasoning to each other often expose misconceptions about when to multiply versus add indices.