KS3 Rounding Worksheets
Approximation (A)
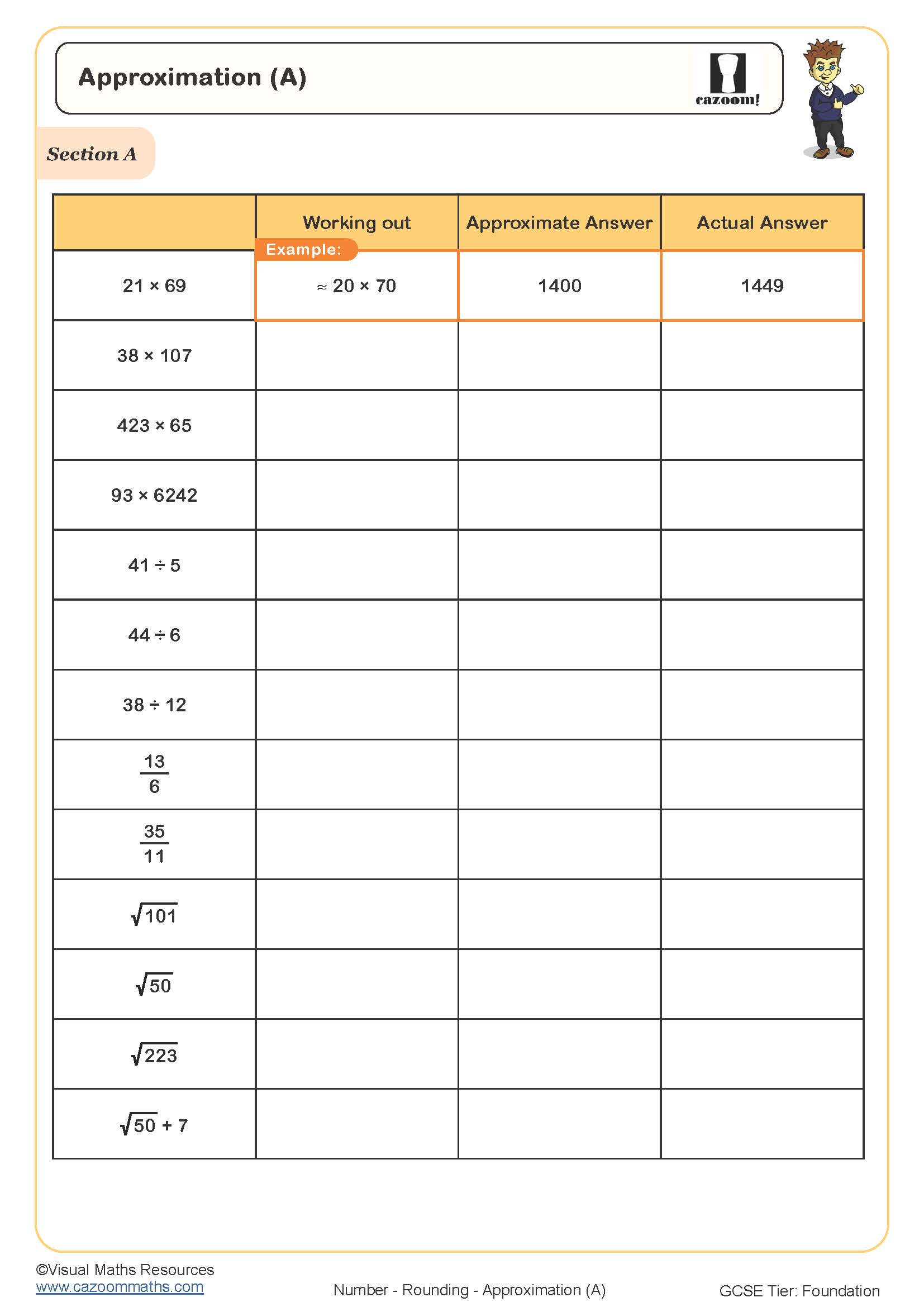
Approximation (B)
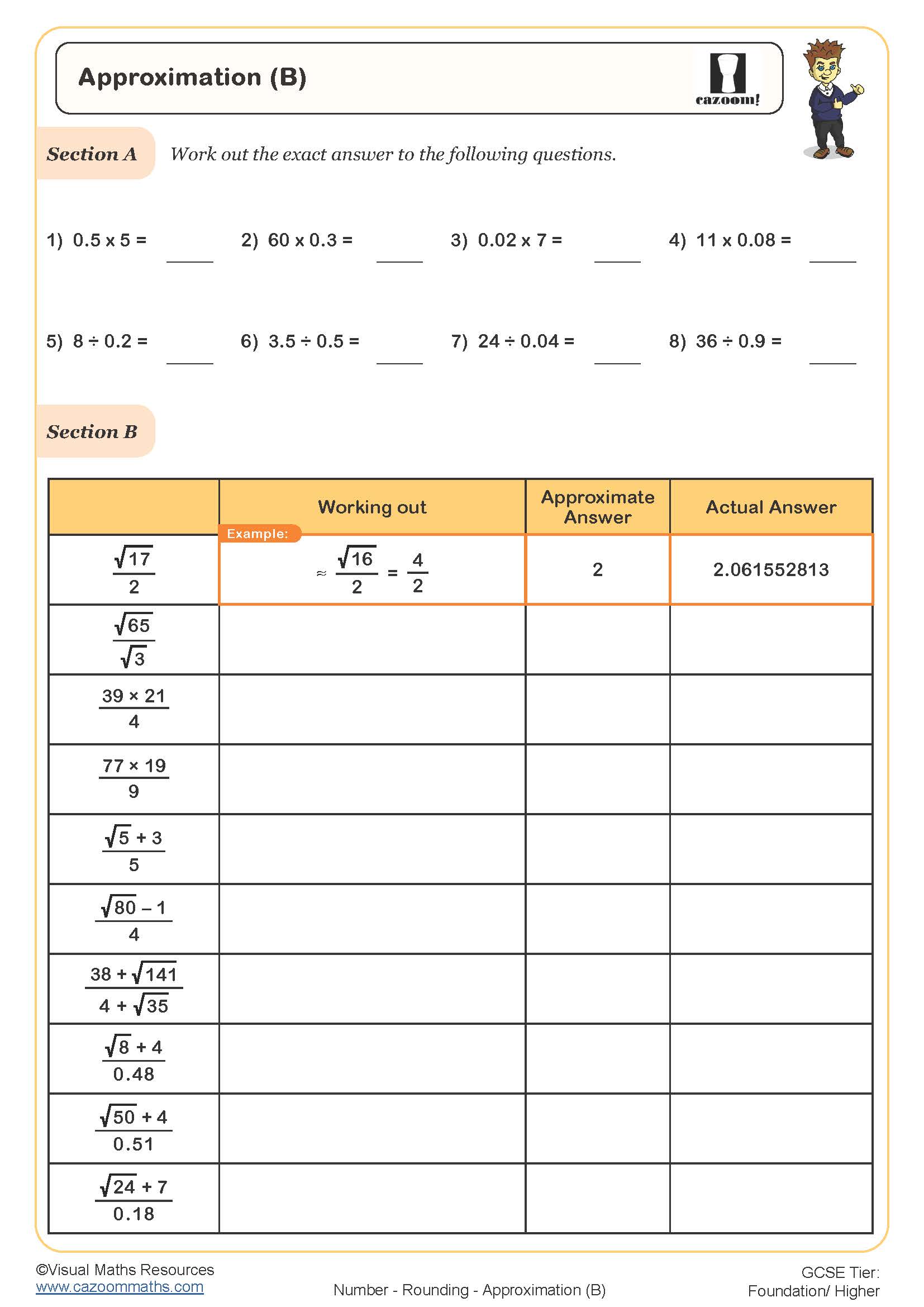
Estimating Powers and Roots
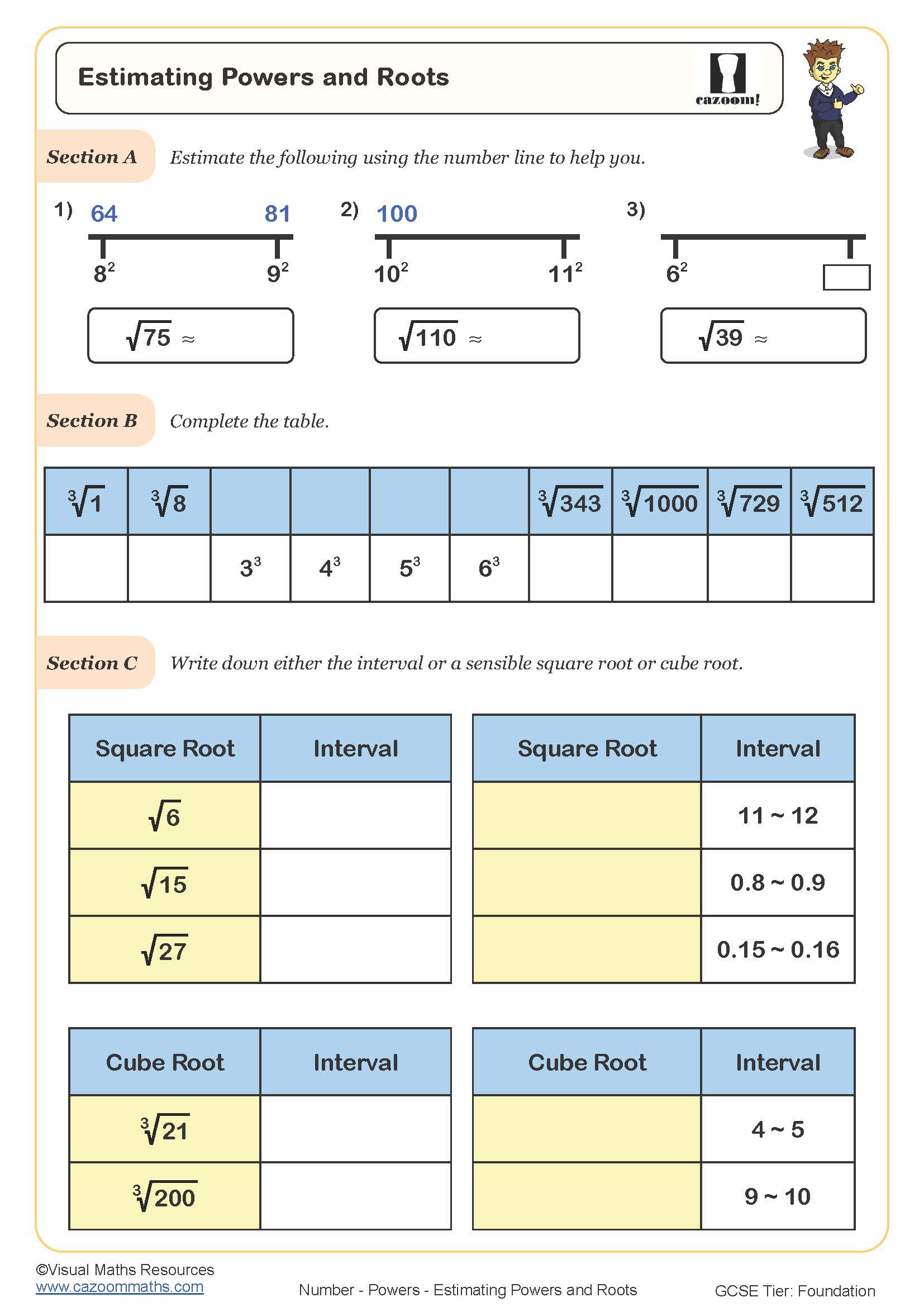
Rounding Charts
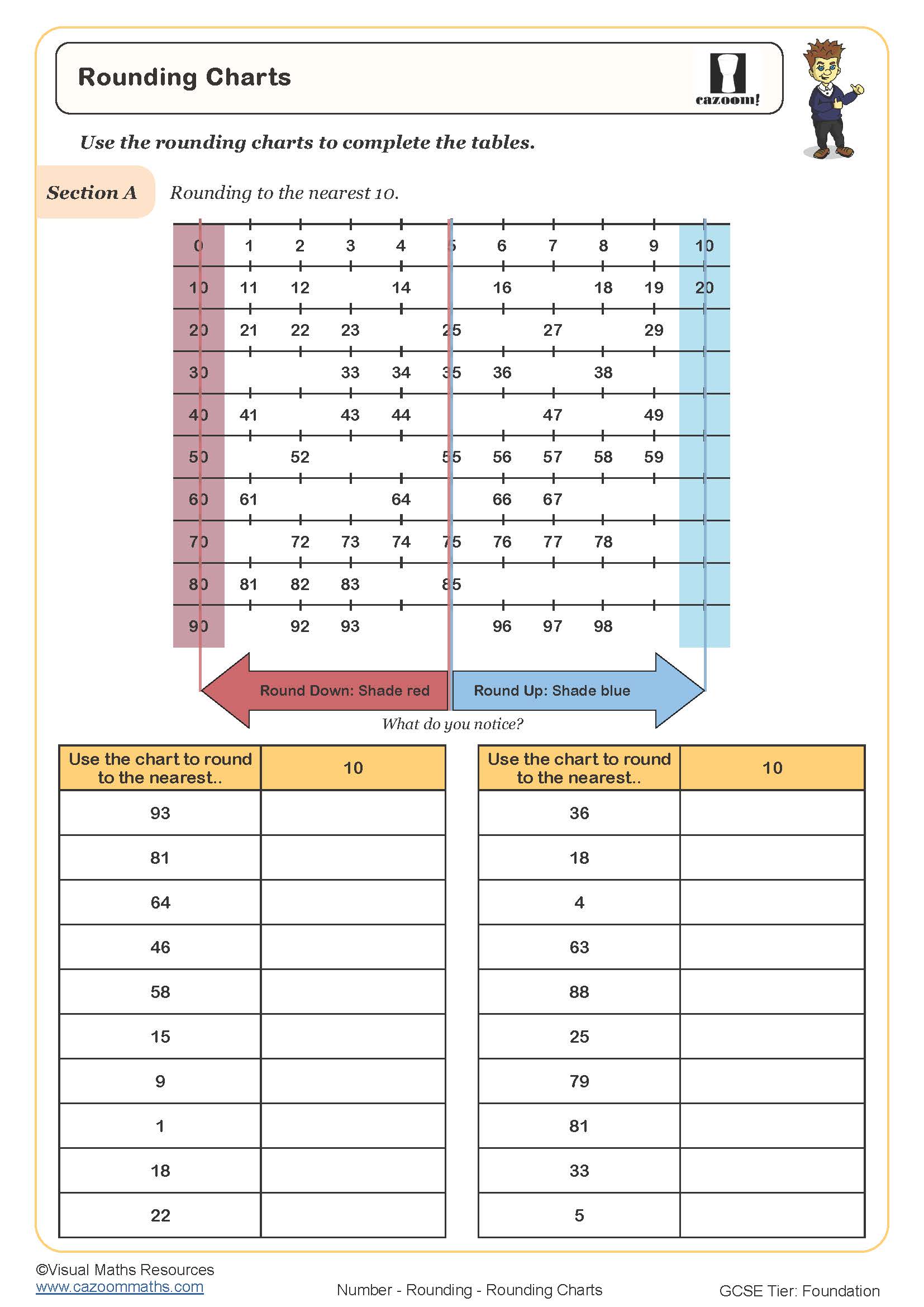
Rounding Mixed Exercise
Rounding to Decimal Places
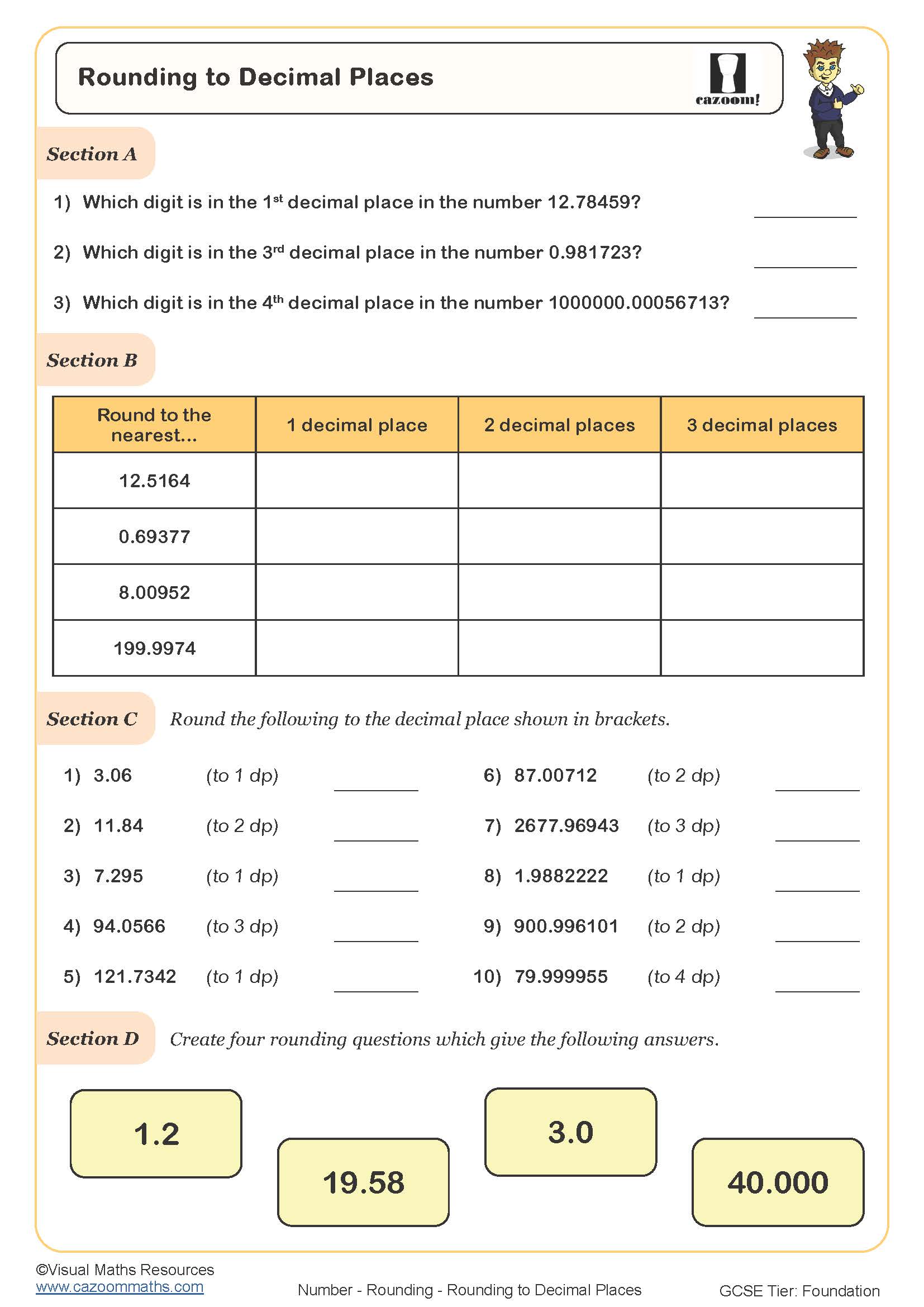
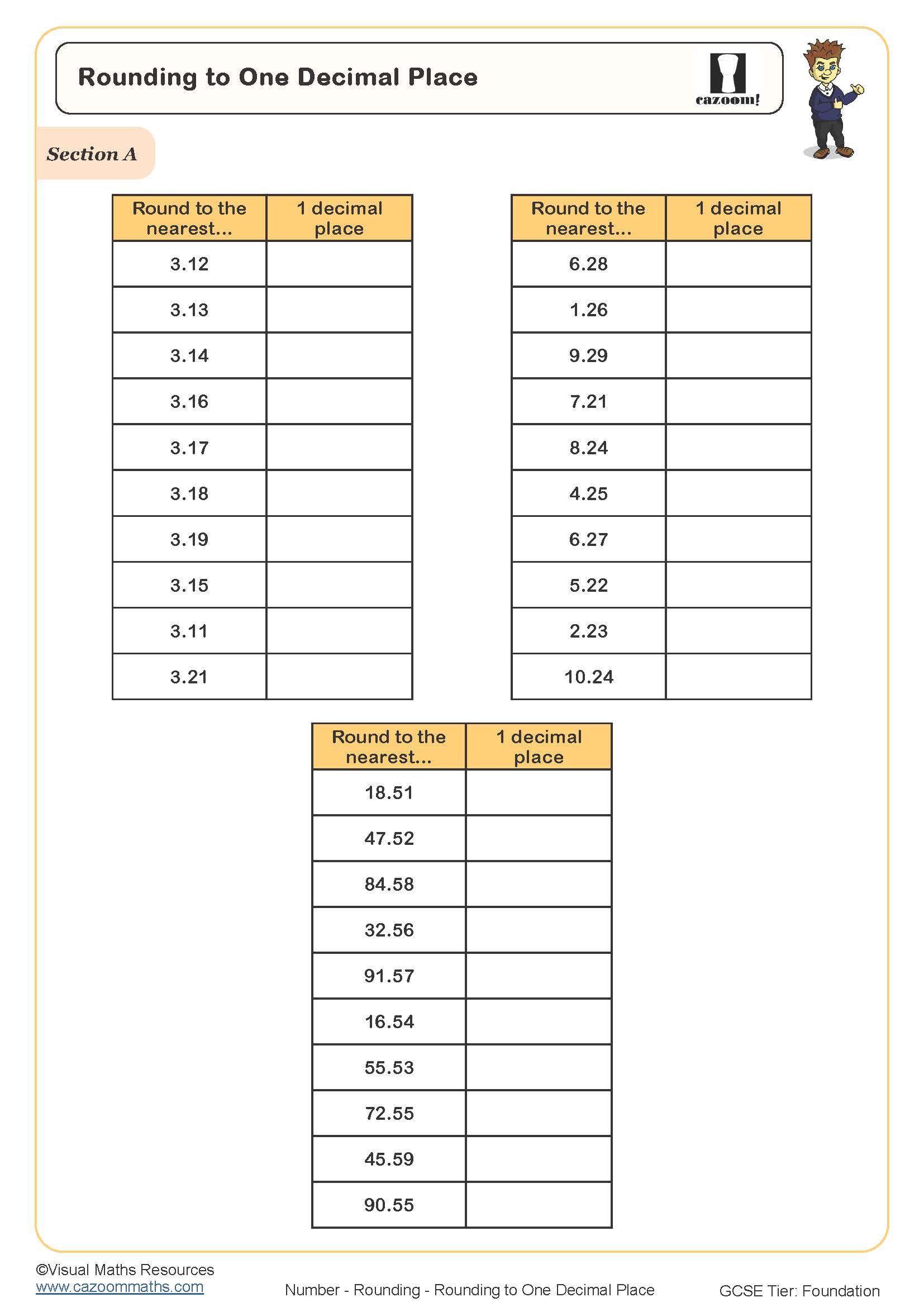
Rounding to One Decimal Place
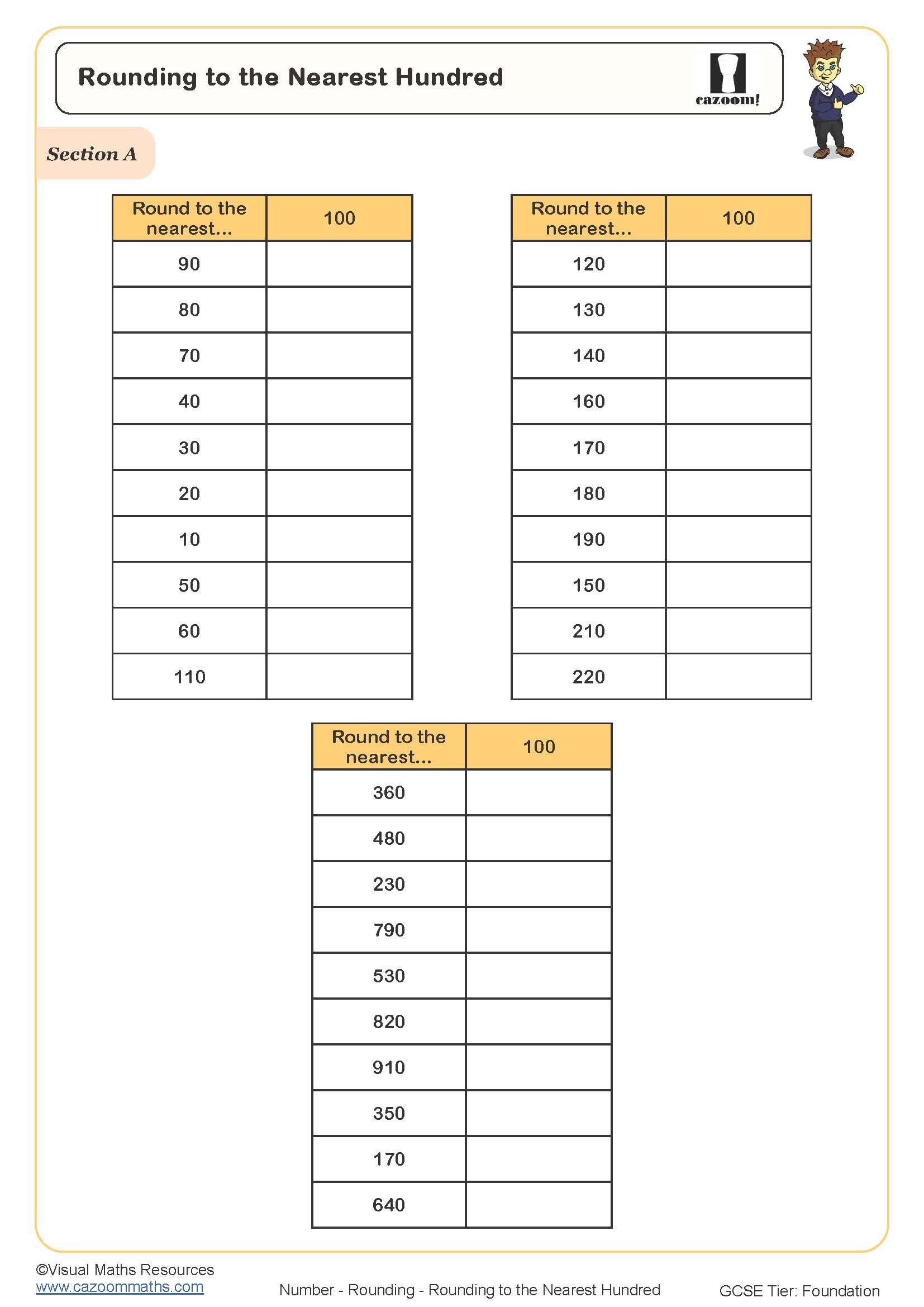
Rounding to the Nearest Hundred
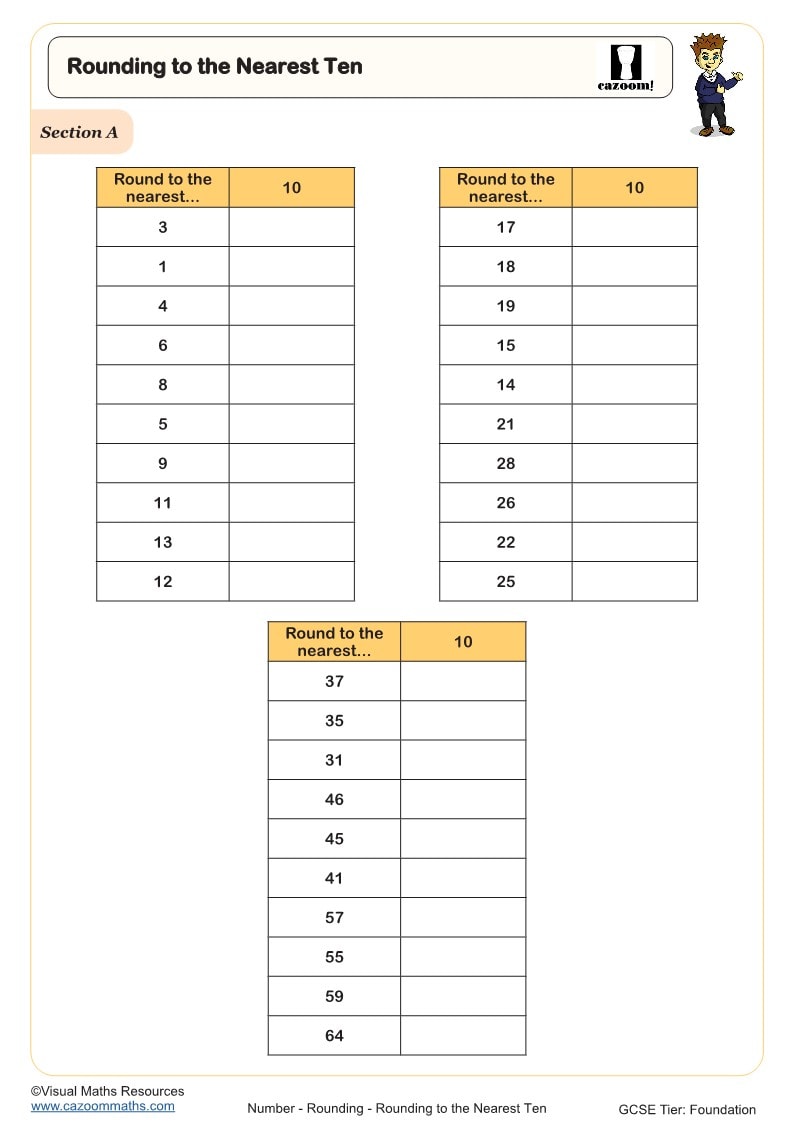
Rounding to the Nearest Ten
Rounding to the Nearest Thousand
Rounding to the Nearest Whole Number
Significant Figures (A)
Significant Figures (B)
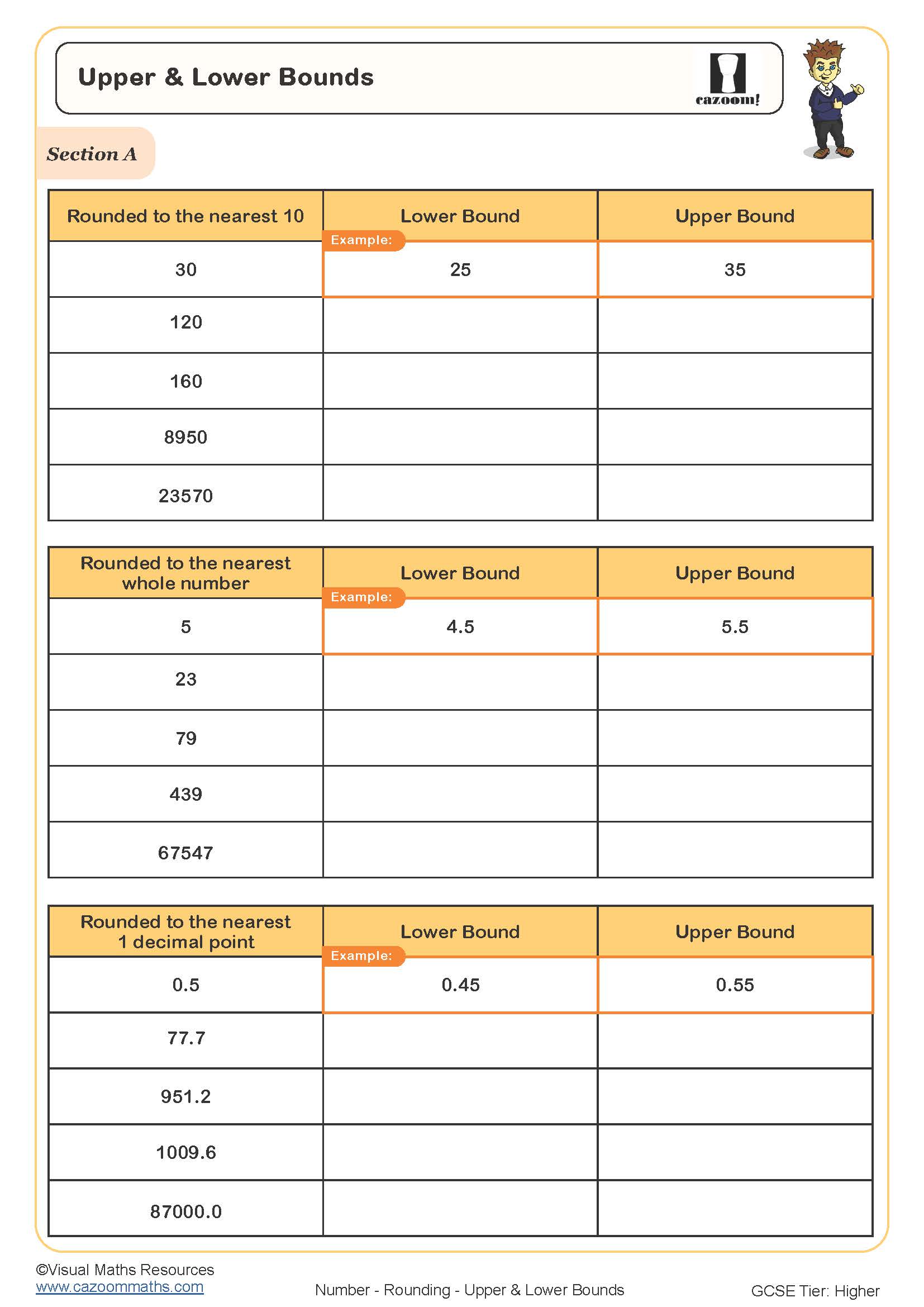
Upper and Lower Bounds
