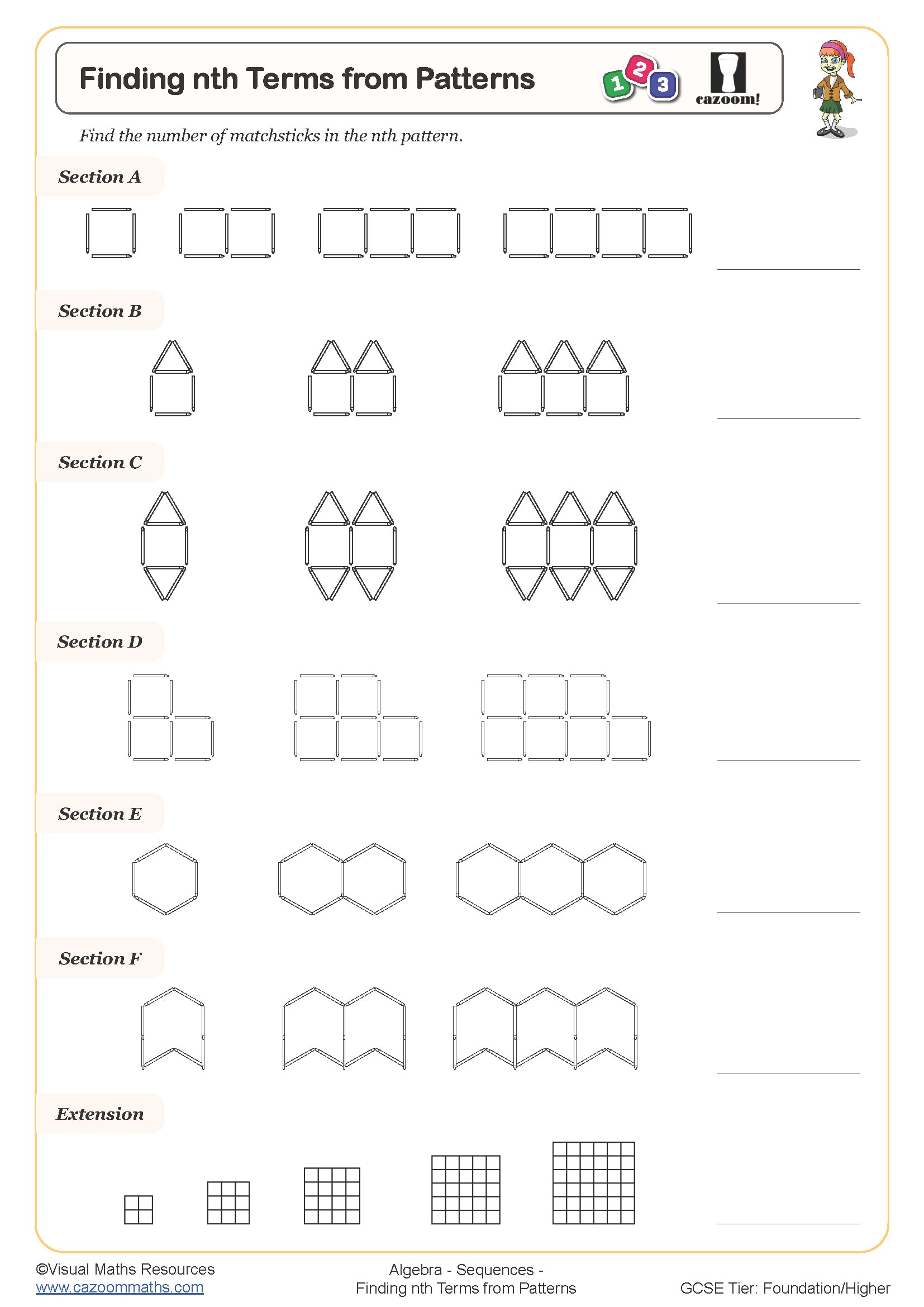
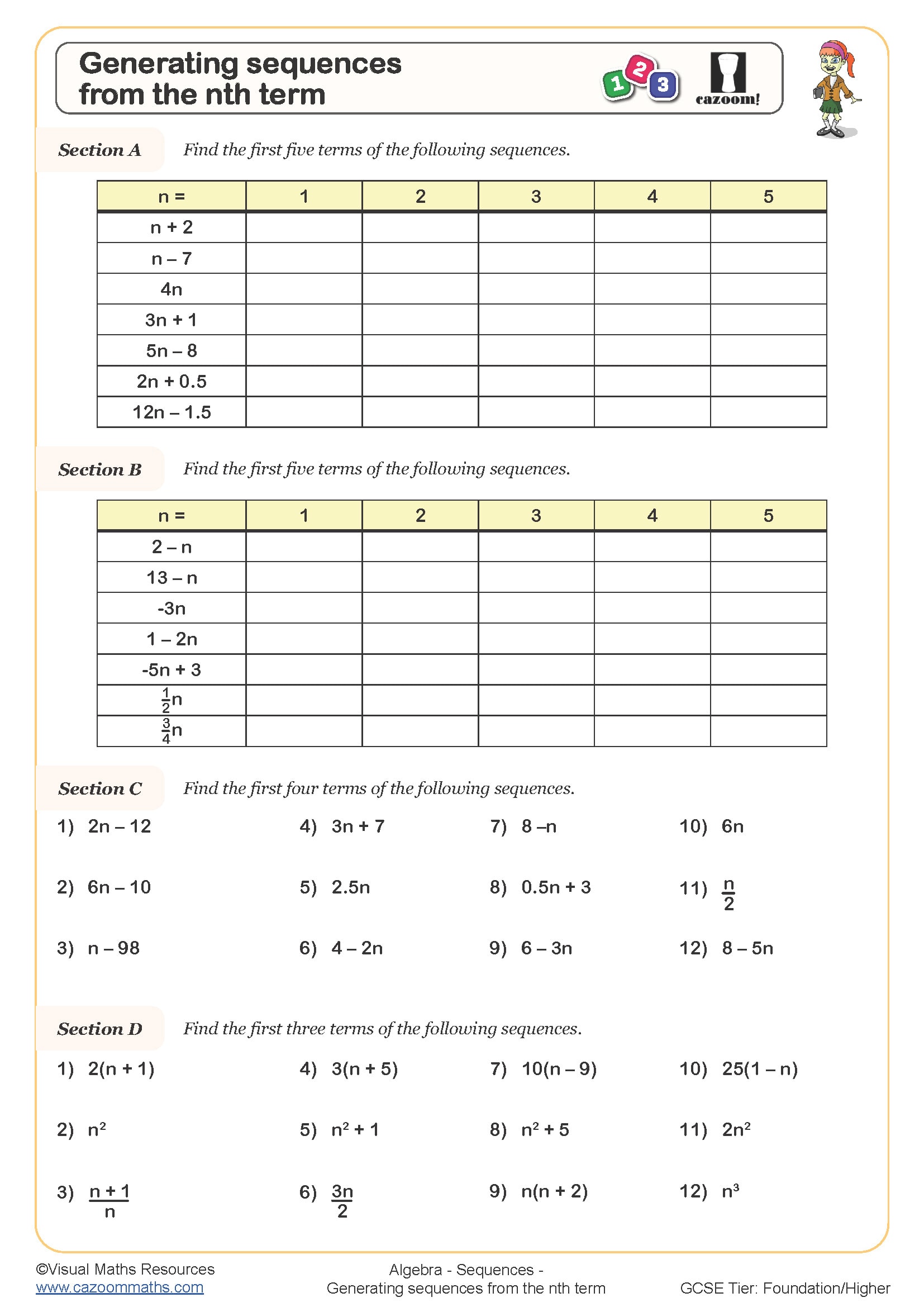
KS3 Sequences Worksheets
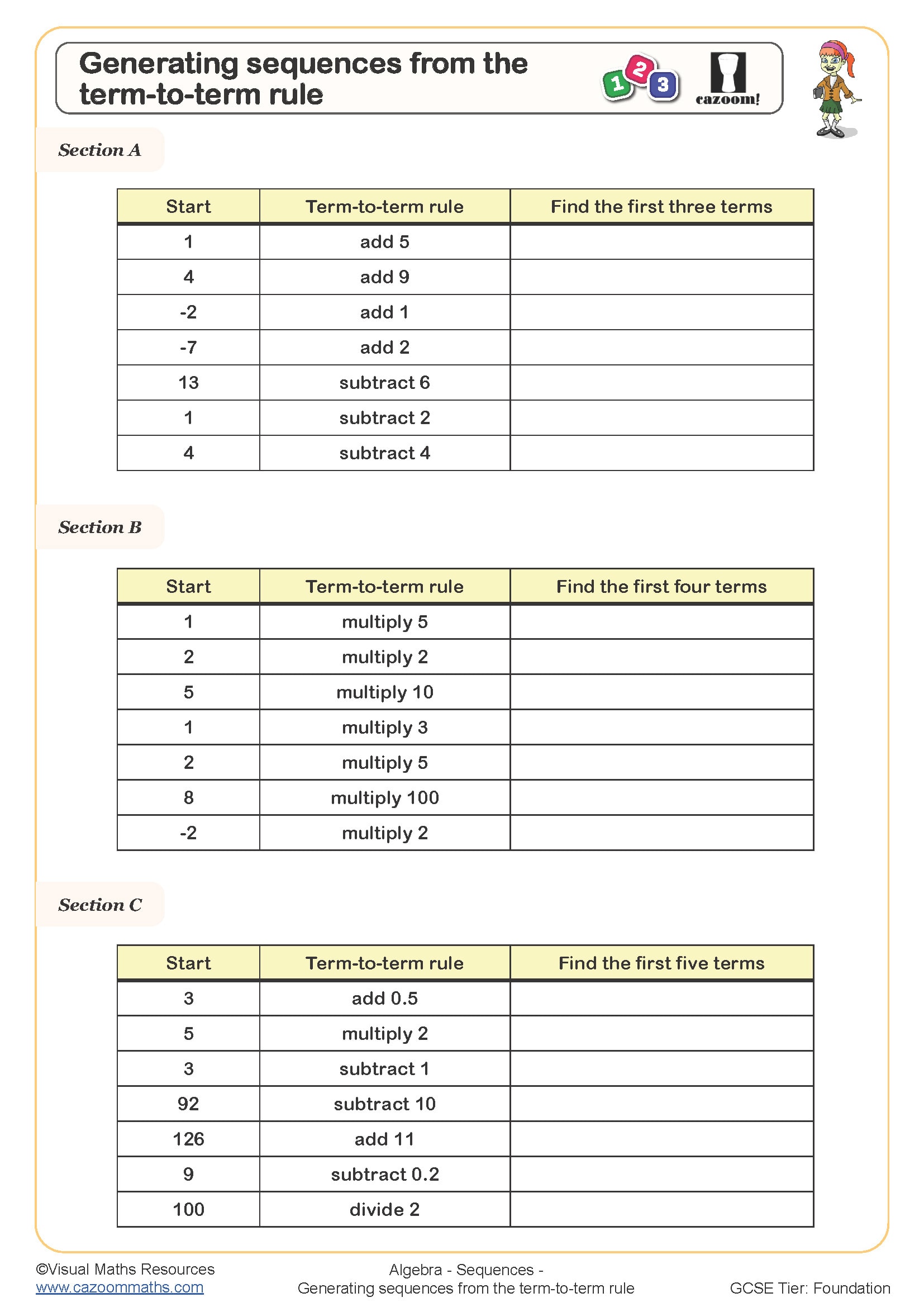
What is a term to term rule worksheet used for?
A term to term rule worksheet focuses on teaching students how to describe the relationship between consecutive terms in a sequence, typically by identifying what operation connects one term to the next. At KS3, students learn to express rules like 'add 3' or 'multiply by 2', which forms the foundation for understanding both arithmetic and geometric sequences before progressing to position-to-term rules.
Students frequently make errors by writing the first term as the rule itself, or by only checking their rule against the first two terms without verifying it works throughout the sequence. Teachers often find that asking students to explicitly write 'to get the next term, I...' helps them articulate the pattern before attempting more formal notation, particularly when working with decreasing sequences where the operation becomes subtraction or division.
Which year groups study sequences at KS3?
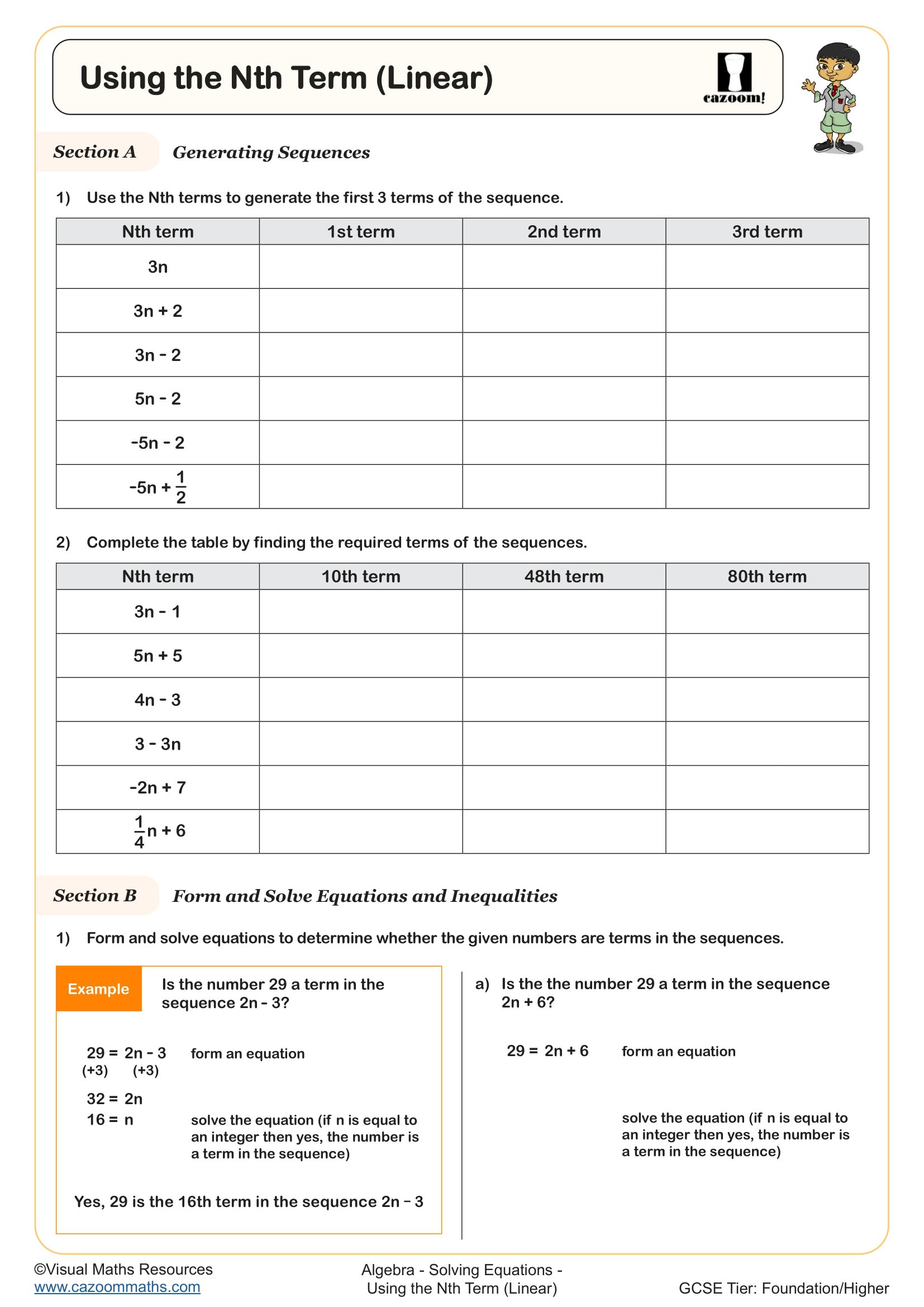
Sequences appear across Year 7, Year 8, and Year 9 in the National Curriculum for KS3, with expectations building progressively. Year 7 students typically begin with simple linear sequences using positive integers, identifying term to term rules and continuing patterns, whilst Year 8 introduces nth term formulae for arithmetic sequences and begins exploring geometric patterns.
By Year 9, students work with more complex arithmetic sequences including those with negative numbers or fractional differences, tackle geometric sequences with confidence, and connect nth term expressions to linear equations. This progression mirrors the algebraic development across Key Stage 3, where pattern recognition gradually becomes formalised through algebraic notation, preparing students for the sequences questions that regularly appear on both Foundation and Higher tier GCSE papers.
What are geometric sequences and why do they matter?
Geometric sequences are patterns where each term is found by multiplying (or dividing) the previous term by a fixed number called the common ratio. Unlike arithmetic sequences that increase by adding a constant difference, geometric sequences grow or shrink multiplicatively, creating patterns like 2, 6, 18, 54 (multiply by 3) or 80, 40, 20, 10 (divide by 2, or multiply by 0.5).
Geometric sequences model exponential growth and decay in real-world contexts across science, finance, and computing. Populations of bacteria doubling every hour, radioactive decay in physics, compound interest calculations, and even digital file compression algorithms all rely on geometric progression. Students who understand these patterns gain insight into why pandemics spread rapidly, how investments grow over time, and why Moore's Law predicted computing power would double regularly, making this topic particularly relevant for STEM pathways.
How do these worksheets help students master sequences?
The worksheets provide structured practise that moves students from recognising patterns to generating terms and eventually deriving rules independently. Questions typically begin with straightforward sequences before introducing variations like negative common differences or decimal multipliers, allowing students to build confidence before tackling more challenging problems that mirror GCSE expectations.
Teachers use these resources flexibly depending on classroom needs: as starter activities to recap prior learning, for differentiated independent work where students select appropriate challenge levels, or as homework to consolidate lesson content. The answer sheets make them particularly valuable for intervention sessions where students can check their own work and identify exactly which types of sequences need further attention, or for peer marking activities that encourage mathematical discussion about methods and common errors.