KS3 Trigonometry Worksheets
What should students practise with trigonometry worksheets?
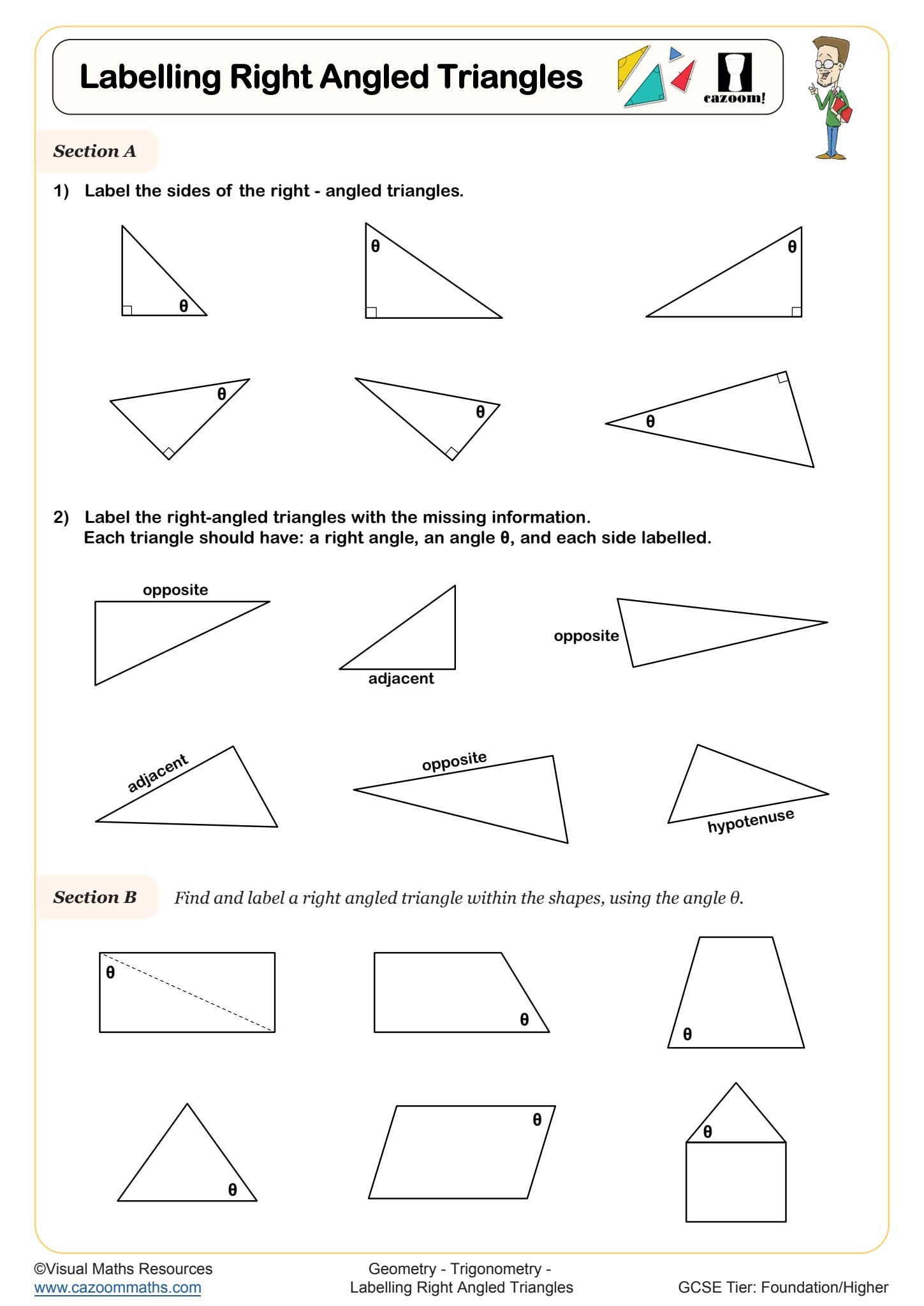
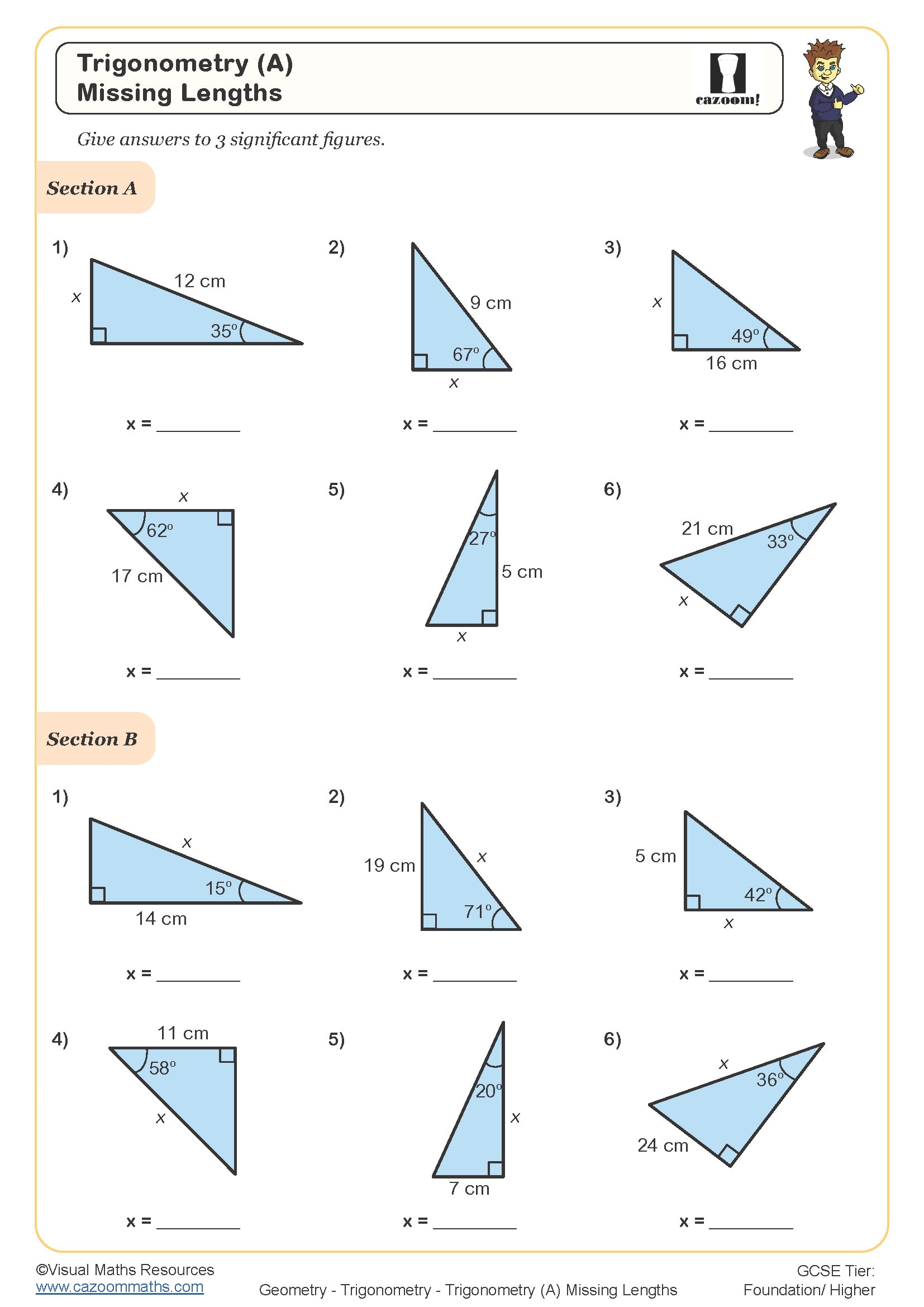
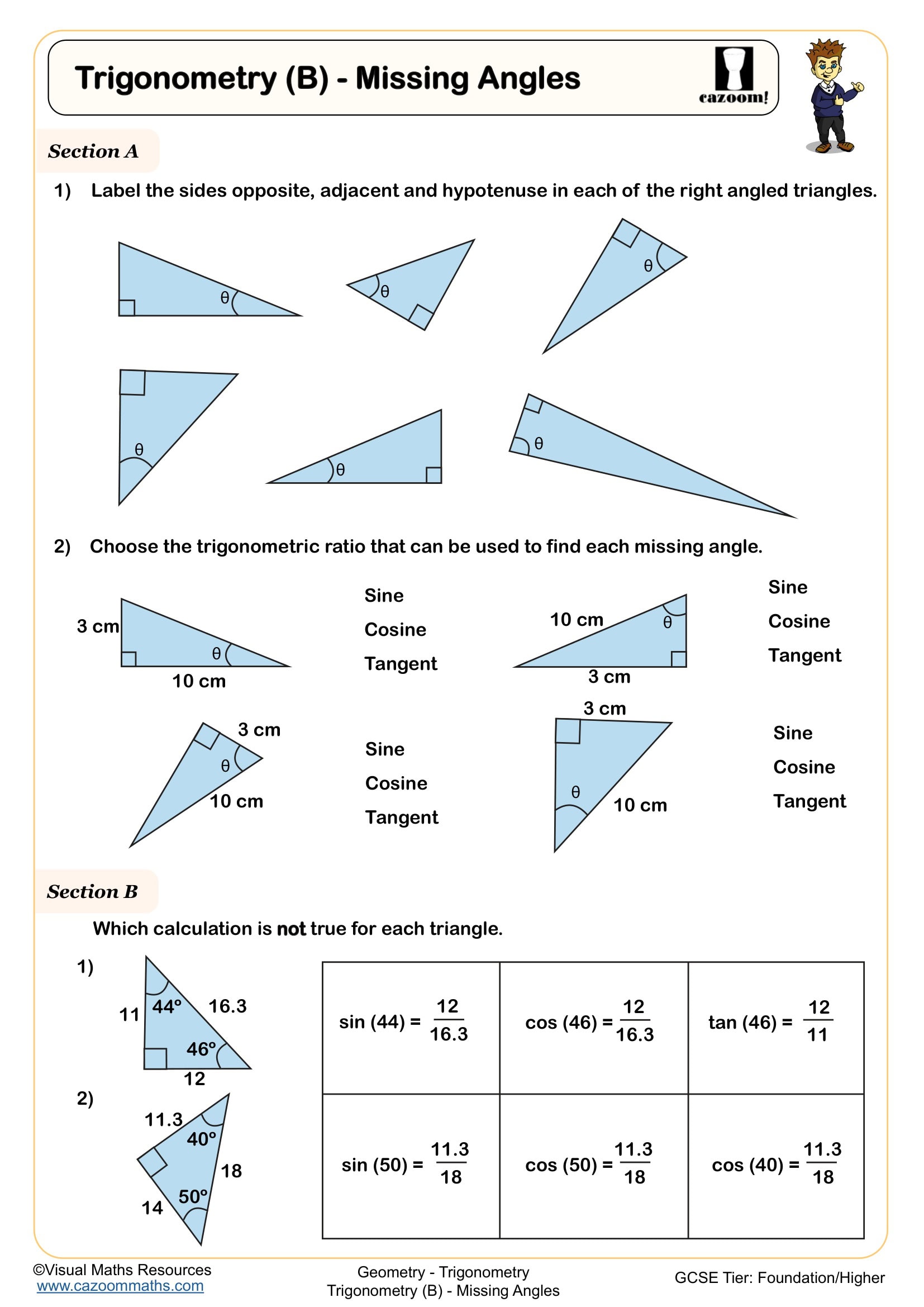
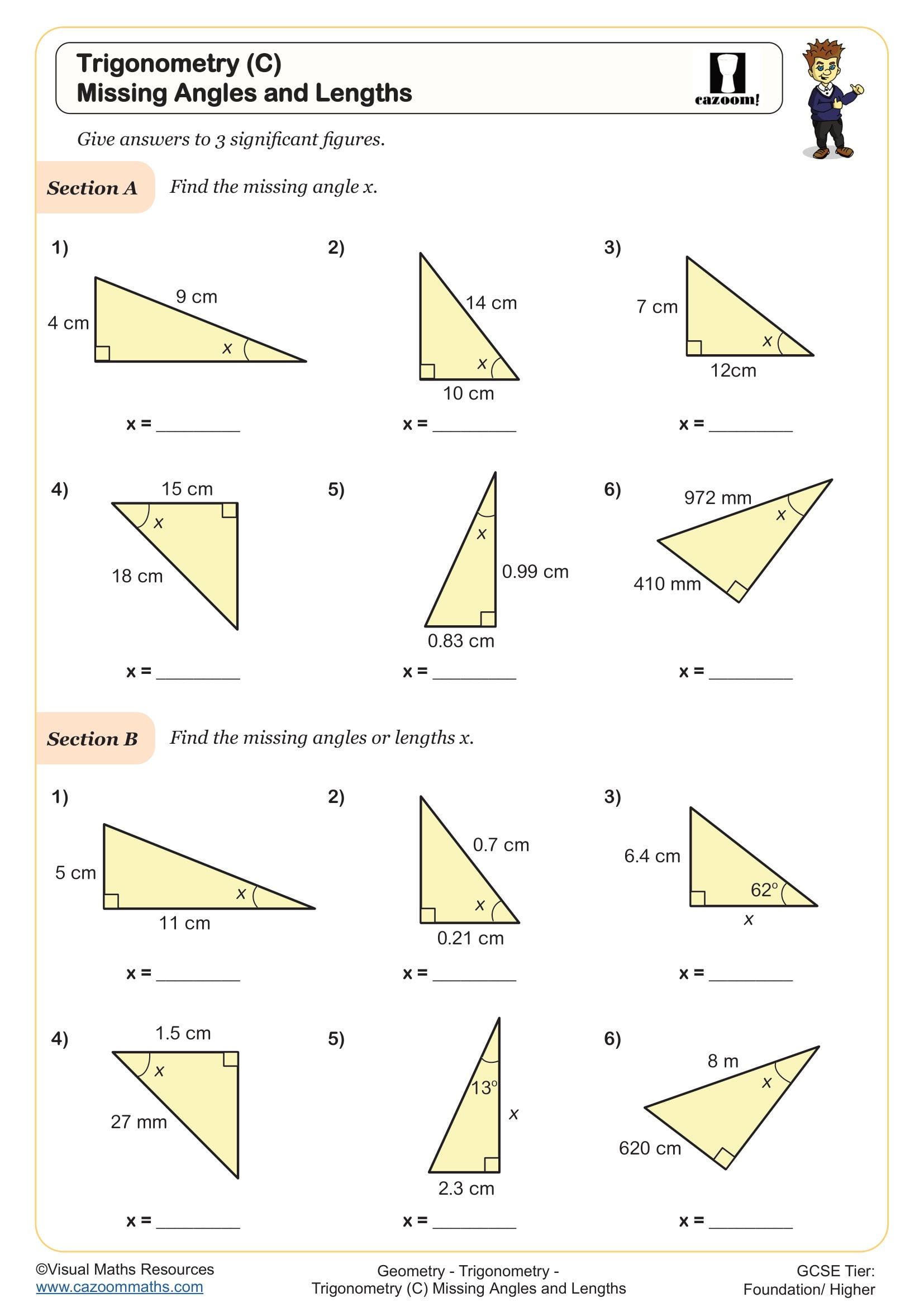
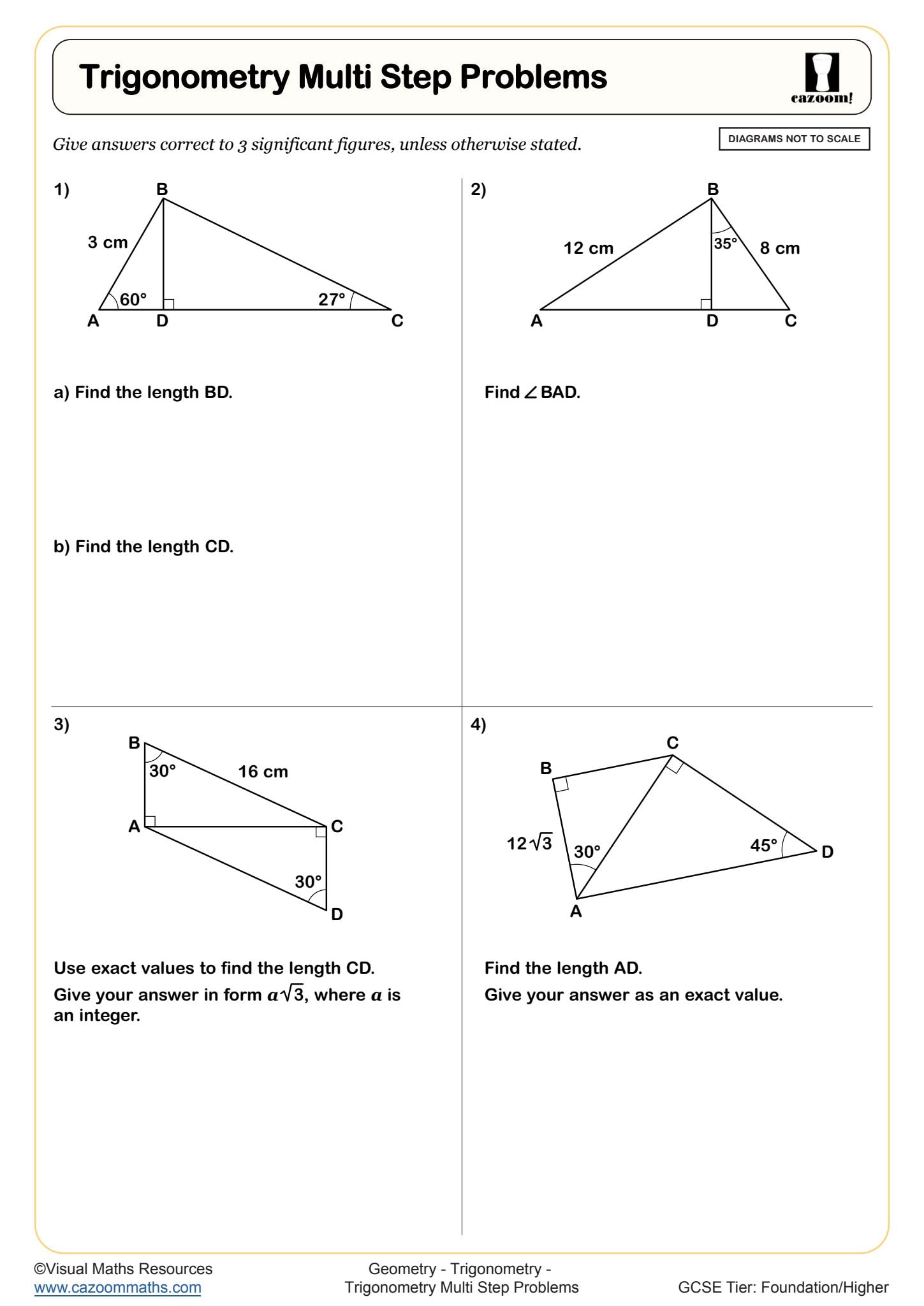
Effective trigonometry worksheets should take students beyond memorising SOH CAH TOA and into fluent application. At KS3, this means identifying which sides of a right-angled triangle are opposite, adjacent and hypotenuse relative to a given angle, then selecting and applying the correct trigonometric ratio. Students need practice finding both missing lengths and missing angles, requiring them to rearrange formulae and use inverse functions on their calculators.
Many students lose marks on exam questions because they've labelled sides incorrectly when the triangle orientation changes. Trig worksheets that present triangles in various positions, not just with the right angle at bottom-right, help students develop the spatial reasoning needed to identify sides correctly regardless of how the diagram appears on the page.
Which year groups study trigonometry at KS3?
These worksheets are designed for Year 8 and Year 9 students following the National Curriculum for England. Trigonometry typically appears in Year 9 for most schools, though some higher-attaining Year 8 groups begin exploring basic trigonometric ratios towards the end of the year. The content bridges Key Stage 3 and GCSE Foundation tier expectations, establishing essential skills that students will refine and extend throughout Key Stage 4.
Progression across these year groups moves from finding one missing length or angle in straightforward diagrams to multi-step problems involving Pythagoras' theorem alongside trigonometry. Year 9 students encounter problems where they must first identify whether they need trigonometry or Pythagoras, then work through cuboids requiring multiple calculations to reach three-dimensional lengths and angles.
How does trigonometry apply to three-dimensional shapes like cuboids?
Working with cuboids introduces students to the reality that many trigonometry problems require breaking a three-dimensional situation into manageable two-dimensional right-angled triangles. To find the angle between a diagonal and the base of a cuboid, students must first use Pythagoras' theorem to calculate the base diagonal, then apply trigonometry using this calculated length and the height. These multi-step problems develop mathematical reasoning and decision-making skills that exam mark schemes specifically reward.
This skill connects directly to careers in construction, architecture and engineering. Structural engineers calculate angles for roof trusses spanning rectangular buildings, architects determine sight lines in stadium seating, and surveyors measure gradients on sloping sites. Understanding how to navigate from three-dimensional problems to two-dimensional calculations underpins spatial problem-solving across STEM fields, making these cuboid problems far more than abstract exercises.
How can teachers use these trigonometry worksheets effectively?
The worksheets work well for building procedural fluency once students understand the conceptual foundation of trigonometric ratios. Teachers often use them after practical activities with clinometers or angle measurers, where students have physically measured heights using trigonometry. The progression from finding lengths to finding angles within each worksheet helps students recognise that inverse operations follow the same logical structure they've used in algebra throughout Key Stage 3.
These resources suit targeted intervention for students who struggle with identifying which ratio applies in different contexts, or as homework to consolidate classroom teaching. The complete answer sheets allow students to self-mark and identify specific calculation errors, whether that's incorrect calculator use for inverse functions or misidentification of opposite and adjacent sides. Many teachers set these worksheets as paired work, with students explaining their ratio choice to a partner before calculating, which surfaces misconceptions before they become embedded.