KS3 Written Methods Worksheets
Addition of 4 and 5-digit Numbers
Column Addition - Decimals (A)
Column Addition - Decimals (B)
Four Operations Word Problems (A)
Four Operations Word Problems (A) (With Clues)
Four Operations Word Problems (B)
Four Operations Word Problems (B) (With Clues)
Four Operations Word Problems (C)
Long and Short Division (A)
Long and Short Division (B)
Money Problems (A)
Money Problems (B)
Practising the Column Method for Long Multiplication (A)
Practising the Column Method for Short Multiplication
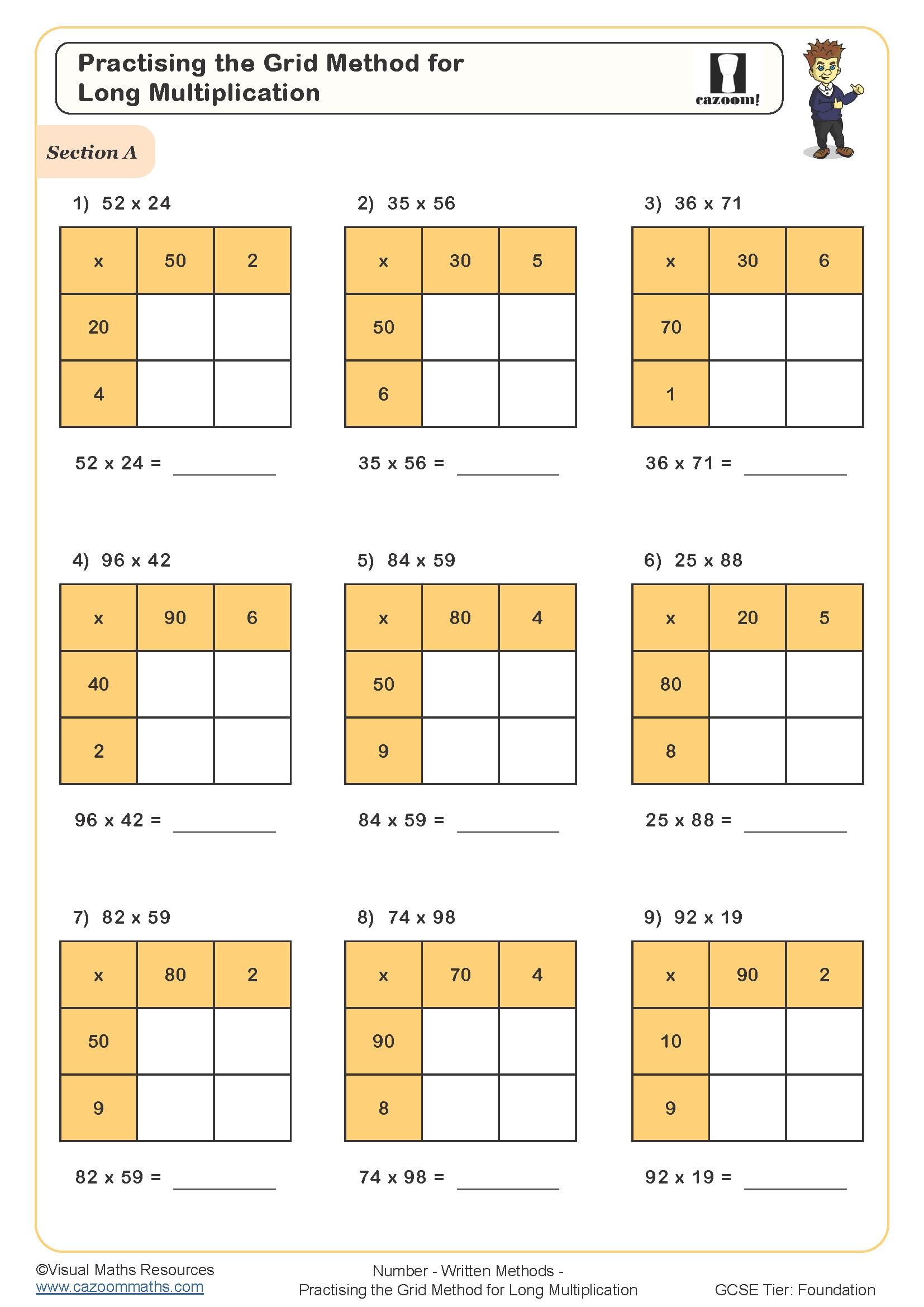
Practising the Grid Method for Long Multiplication
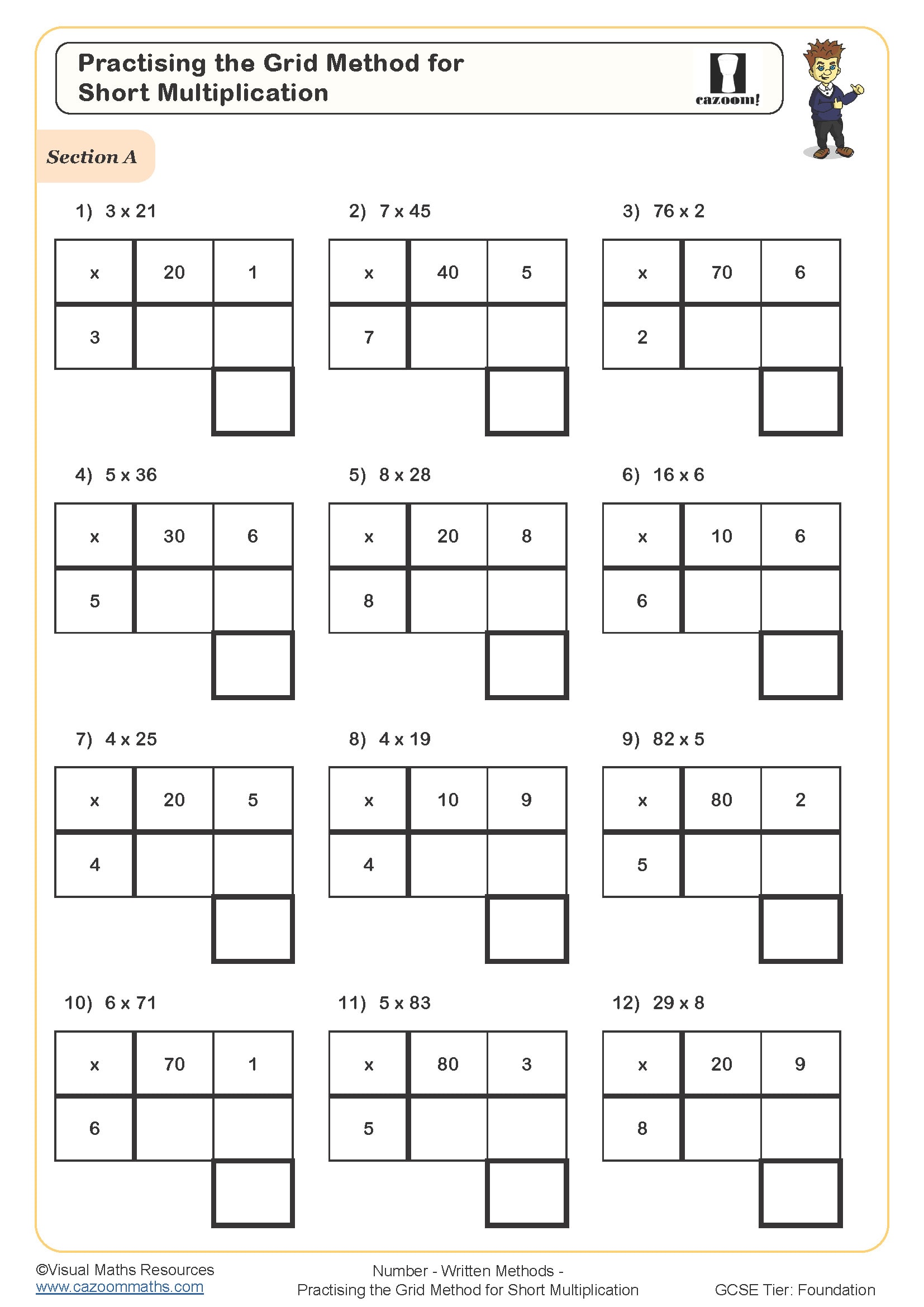
Practising the Grid Method for Short Multiplication (A)
Short Division (A) Dividing 2 Digit Numbers
Short Division (B) Dividing 3 Digit Numbers
Short Division (C) Dividing 2, 3 and 4 Digit Numbers
Short Division (D) Dividing 4 Digit Numbers
Subtraction of 4 and 5-digit Numbers
Use Formal Methods For Addition of Integers
Use Formal Methods For Subtraction of Integers
