KS4 Functions Worksheets
What are functions in GCSE maths?
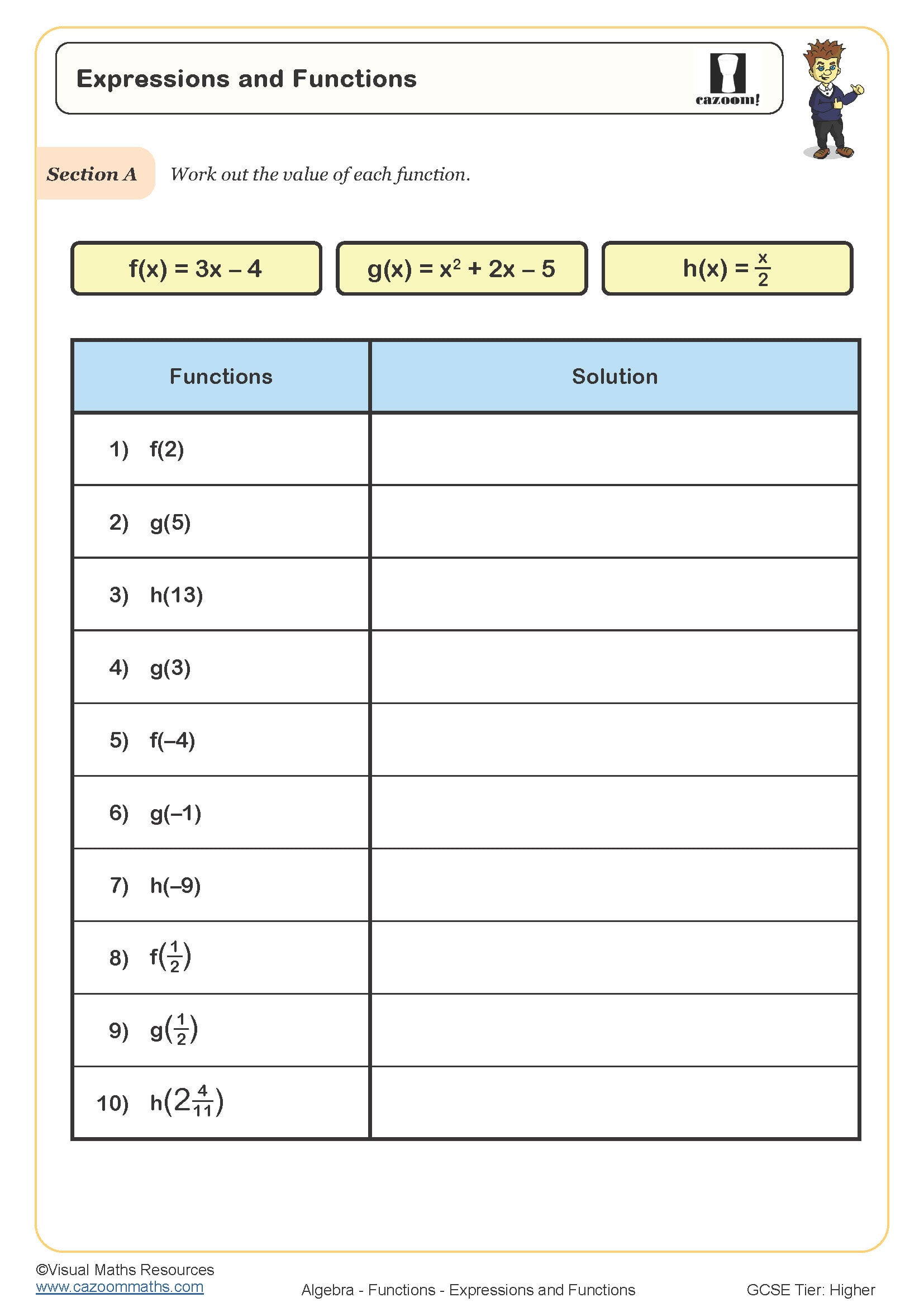
In GCSE mathematics, a function is a mathematical relationship where each input has exactly one output, written as f(x) = expression. Students encounter function notation from Year 10 onwards, learning to evaluate functions, find composite functions like fg(x), and determine inverse functions. The National Curriculum requires students to understand functions as mappings and represent them using diagrams, equations, and graphs.
Teachers often notice students confuse f(2) with f × 2, leading to completely incorrect solutions. When a question asks for f(3) where f(x) = 2x + 5, students might write 2f + 5 instead of substituting the value to get 2(3) + 5 = 11. Exam mark schemes penalise this heavily, as it shows fundamental misunderstanding of function notation as a process rather than multiplication.
Which year groups study functions?
Functions worksheets are available for Year 10 and Year 11 students working at KS4 level. Function notation typically appears first in Year 10, where students learn to evaluate simple functions and understand the concept of input and output. This forms part of the algebra strand in the National Curriculum and features in both Foundation and Higher tier GCSE papers, though Higher tier questions involve more complex composite and inverse functions.
The progression from Year 10 to Year 11 involves moving from evaluating single functions with straightforward substitution to working with composite functions fg(x), finding inverse functions, and solving equations involving functions. Year 11 students encounter non-linear functions including quadratic and reciprocal functions, requiring them to handle more sophisticated algebraic manipulation while maintaining accurate function notation throughout their working.
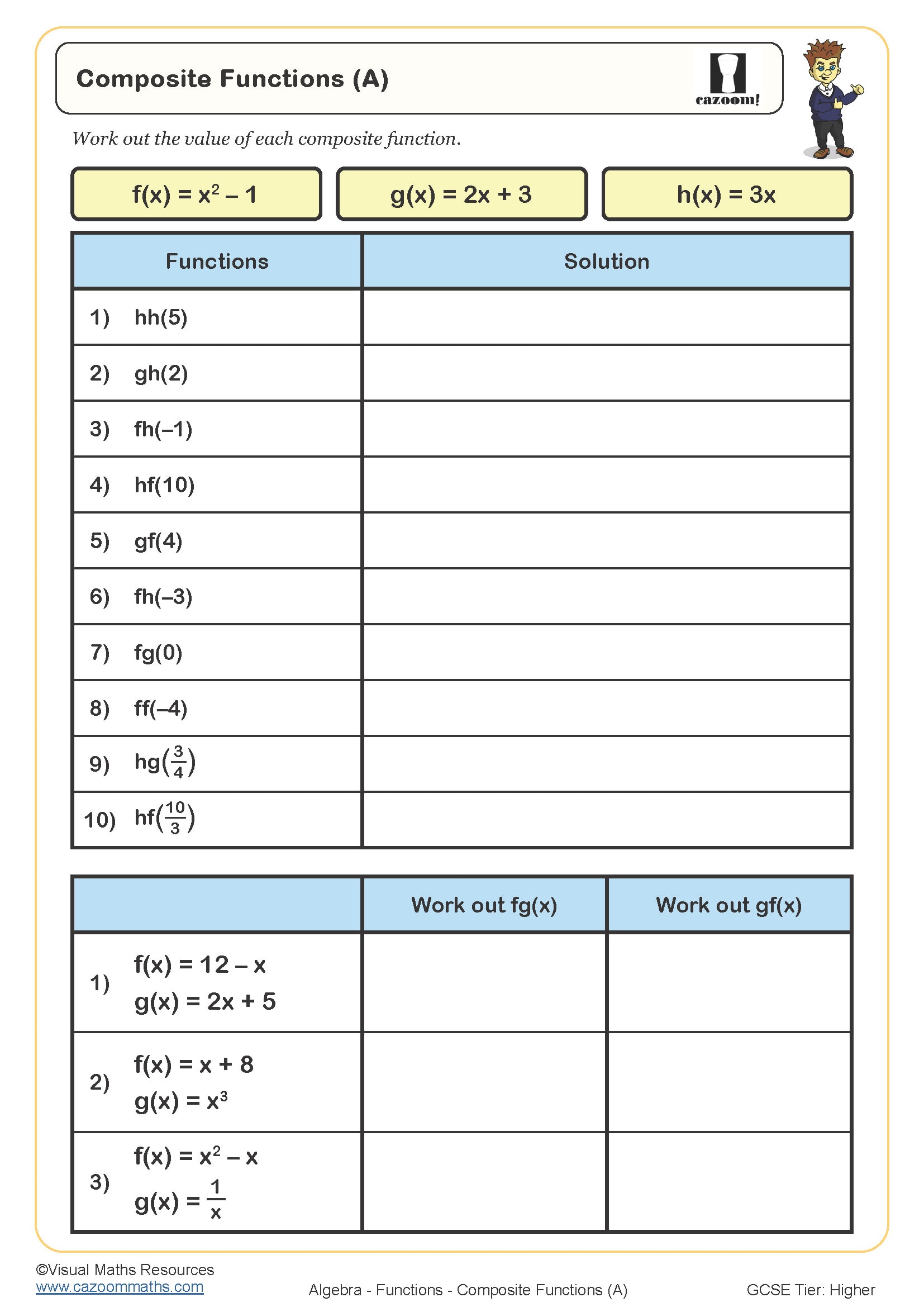
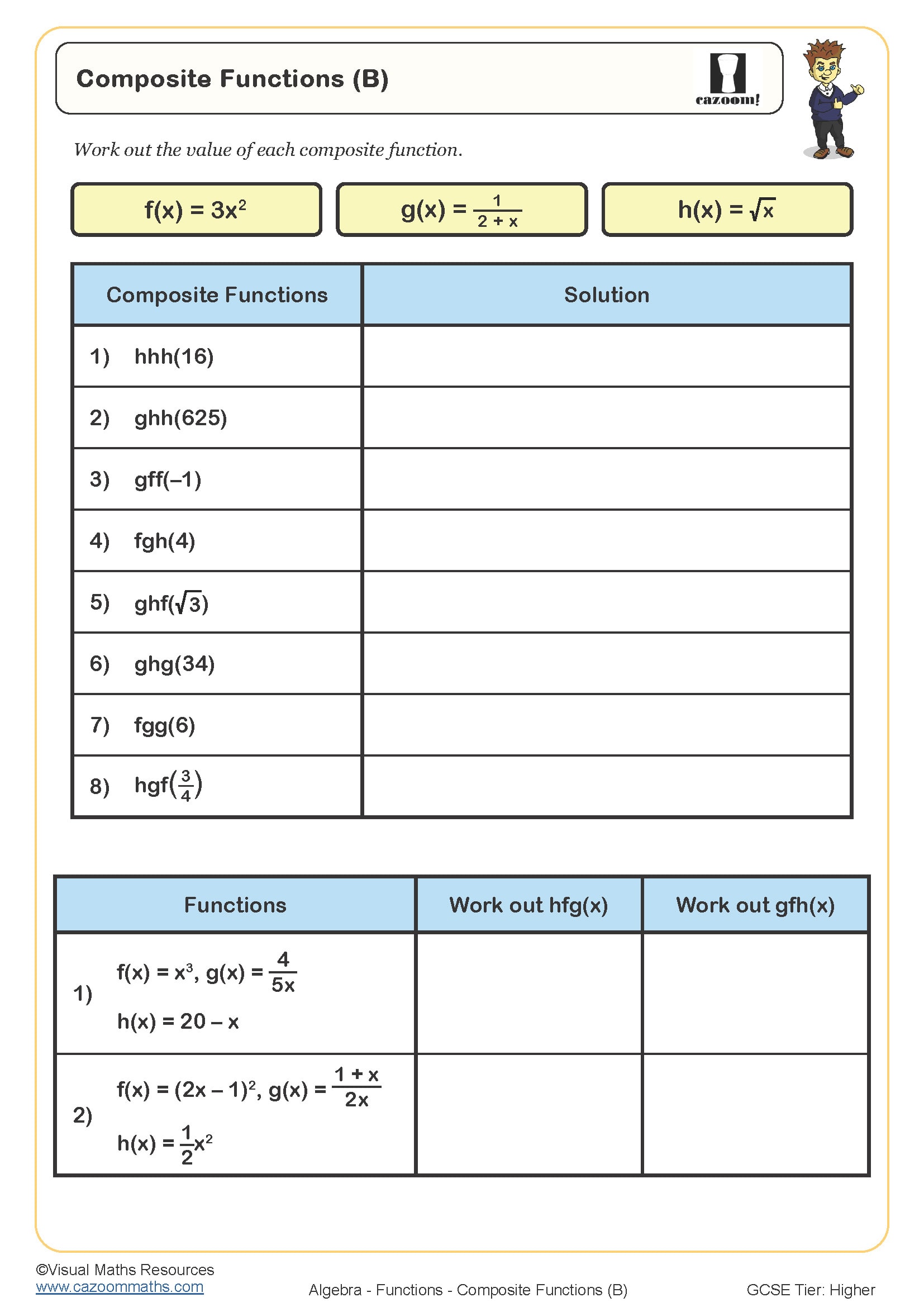
How do composite functions work?
A composite function combines two functions by using the output of one as the input for another. For fg(x), students first apply g to x, then apply f to that result. If g(x) = x + 3 and f(x) = 2x, then fg(x) means f(x + 3) = 2(x + 3) = 2x + 6. Many teachers find that students attempt to multiply functions together rather than performing this substitution process, particularly when working under exam pressure.
Composite functions appear extensively in computer programming and data processing, where information passes through multiple transformations. When encoding data for secure transmission, programmers apply encryption functions sequentially - the output from one encryption layer becomes the input for the next. This layered approach mirrors exactly how fg(x) works, demonstrating why understanding function composition matters beyond pure mathematics and into practical STEM applications.
How should teachers use these function worksheets?
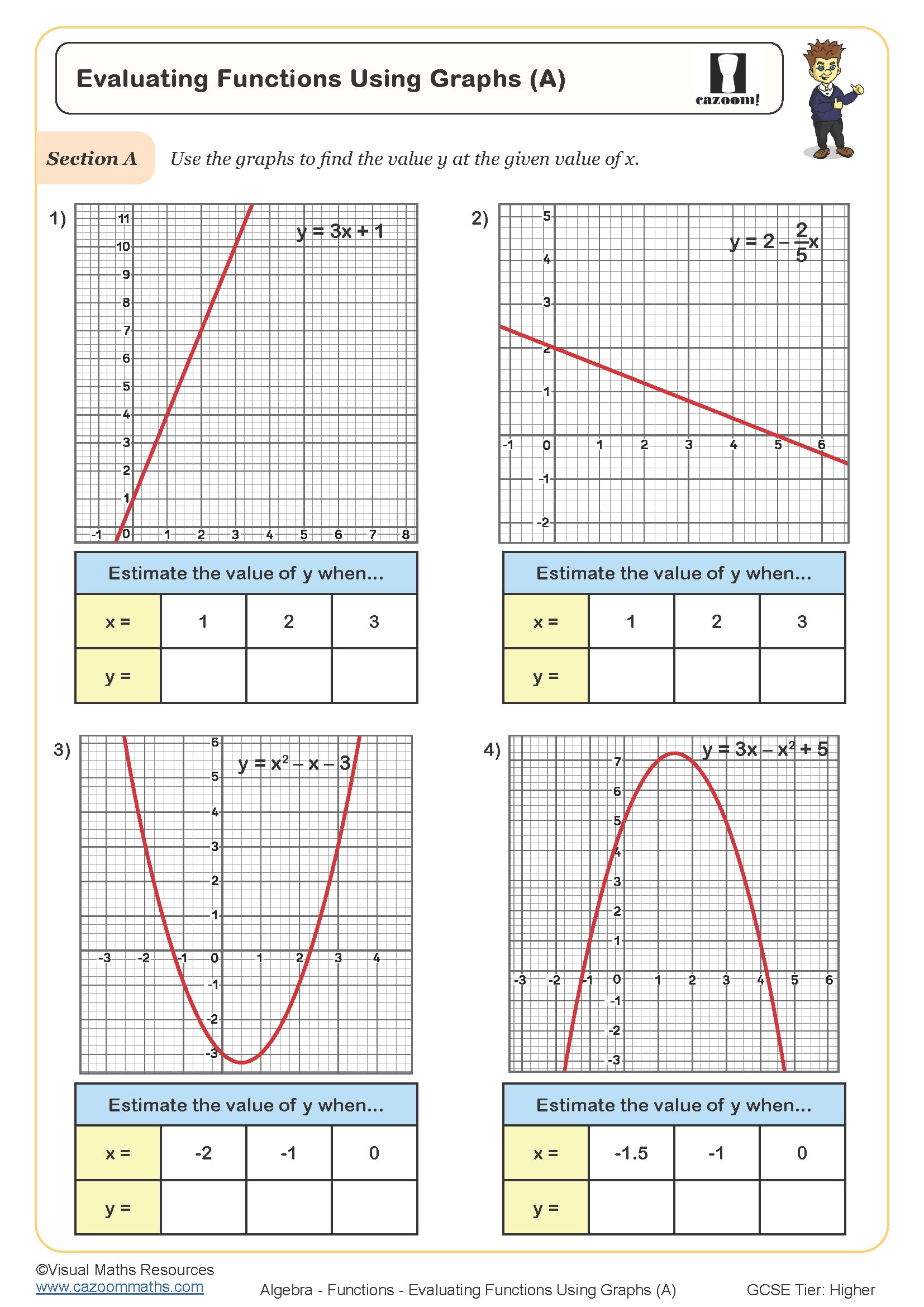
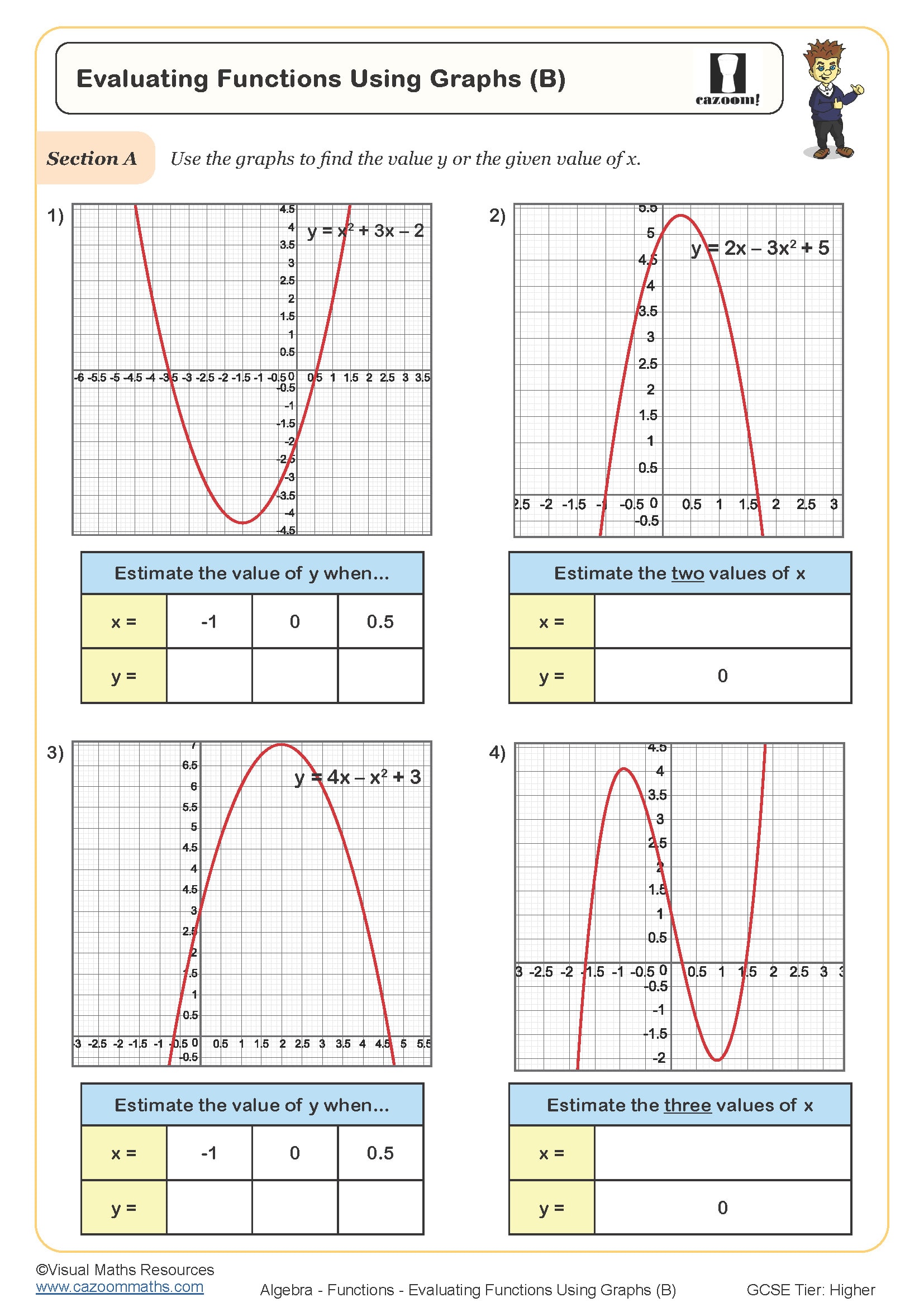
The worksheets provide structured practice that builds from evaluating simple functions to more complex composite and inverse function problems. Card sort activities work particularly well for helping students develop conceptual understanding before tackling algebraic questions, as they require matching and reasoning rather than immediate calculation. The inclusion of non-linear functions ensures students don't develop the misconception that all functions produce straight-line graphs.
Teachers typically use these worksheets for targeted intervention when students struggle with function notation after initial teaching, or as homework to reinforce classroom learning. The complete answer sheets allow students to self-mark and identify specific areas where they're making errors, whether that's substitution mistakes, sign errors, or misunderstanding the order of operations in composite functions. Paired work using the card sorts encourages mathematical discussion, helping students articulate their understanding of what functions actually represent.