KS4 Inequalities Worksheets
-Worksheet.jpg)
-without-sketching-Questions.jpg)
-satisfying-two-inequalities-Worksheet.jpg?w=3840)
What are the common mistakes when solving inequalities?
The most frequent error occurs when students multiply or divide both sides of an inequality by a negative number but forget to reverse the inequality sign. For example, when solving -2x > 6, students correctly divide by -2 to get x but write x > -3 instead of x < -3. This misconception stems from equation-solving habits where the operation doesn't affect the equals sign.
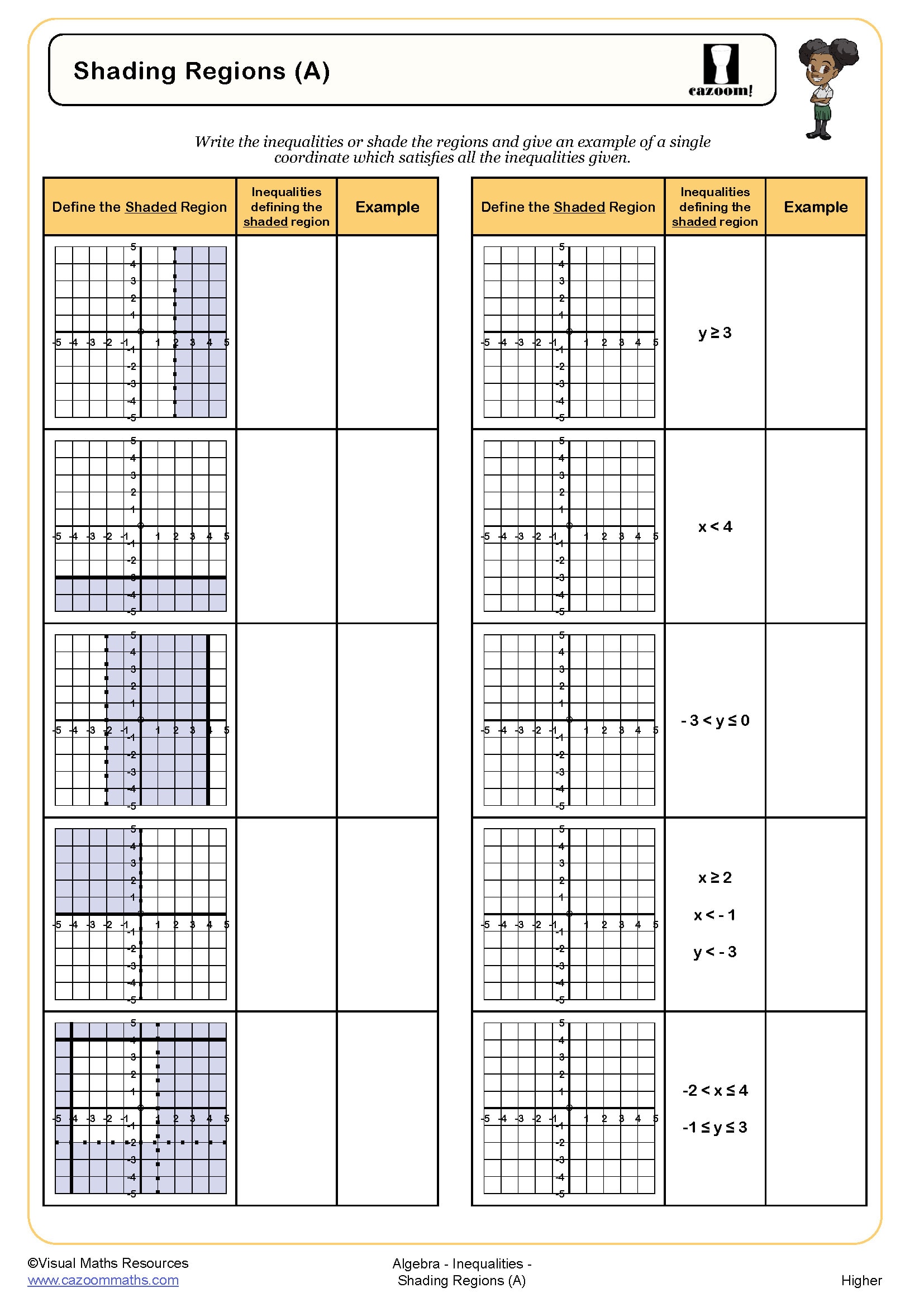
Another common pitfall involves representing solutions on number lines. Students often use open circles for strict inequalities (< or >) but then shade the wrong direction, or they mix up whether the circle should be filled or hollow when dealing with ≤ or ≥. Exam mark schemes consistently penalise incorrect notation here, even when the algebraic working is sound. Teachers find that explicit practice with inequality notation alongside equation work helps students recognise the crucial differences.
Which year groups study inequalities at KS4?
These inequalities worksheets are designed for Year 10 and Year 11 students following the KS4 National Curriculum. Inequalities typically appear in Year 10 as an extension of equation-solving skills, with students learning to manipulate and represent simple linear inequalities before progressing to more complex scenarios involving multiple conditions.
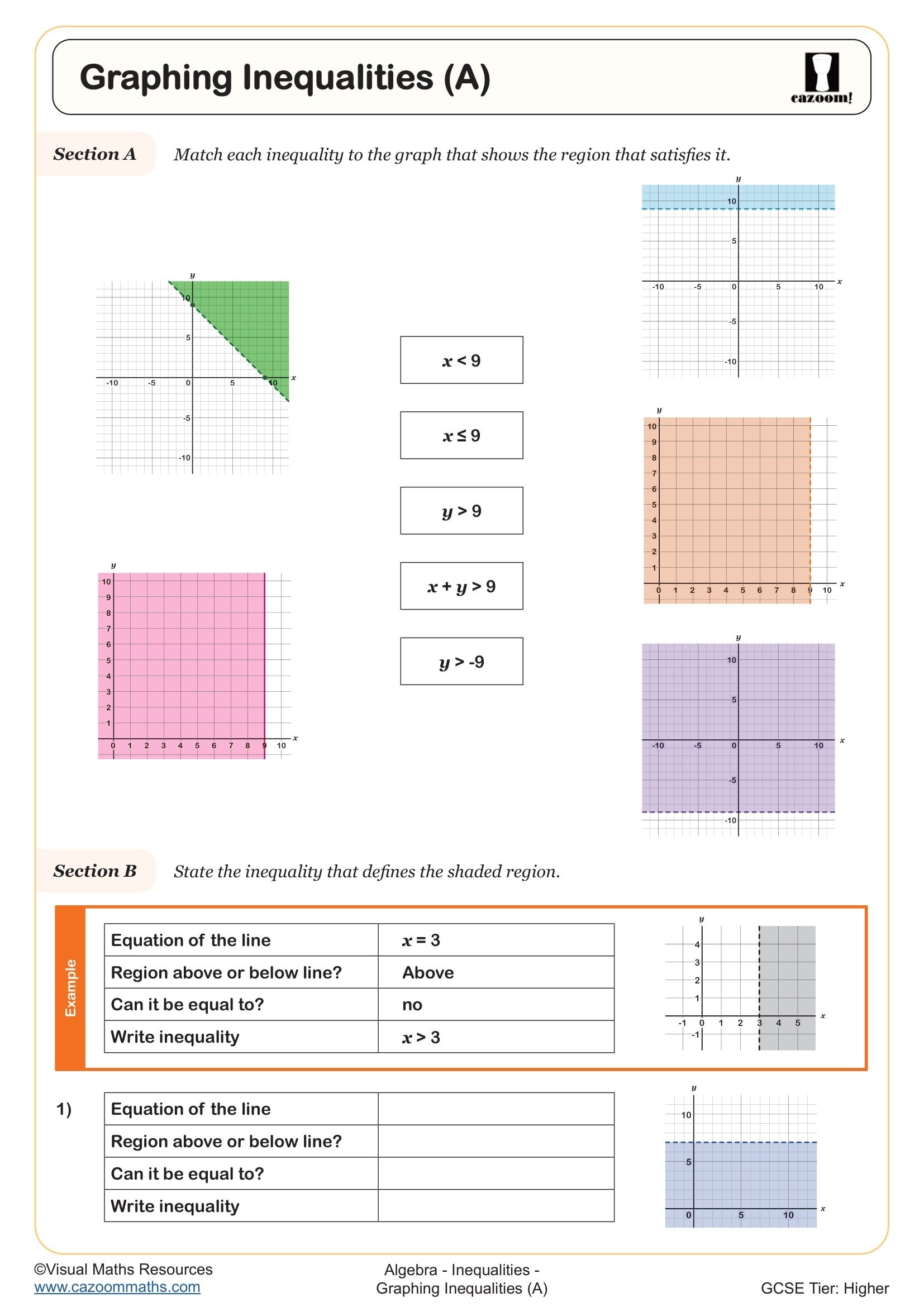
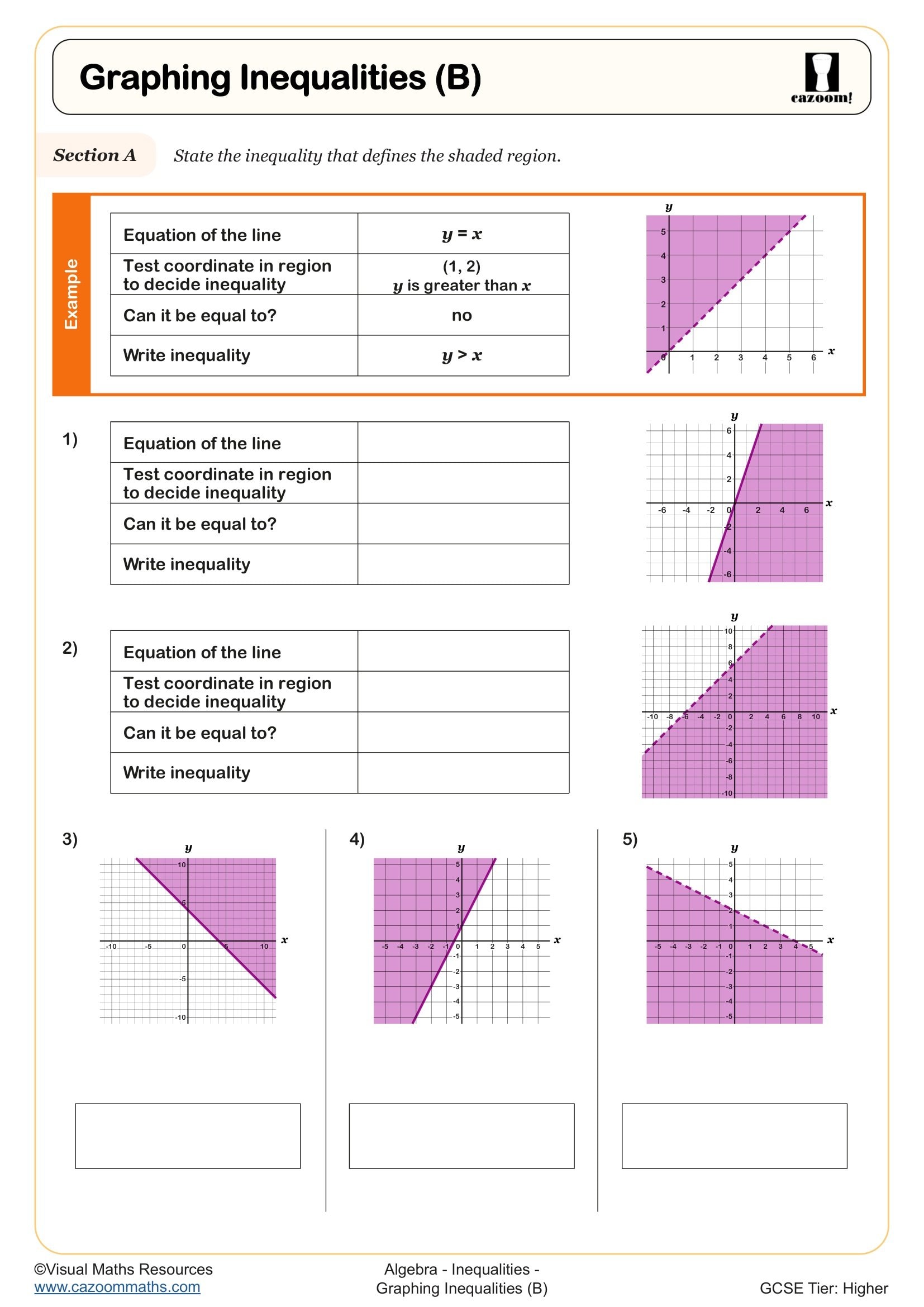
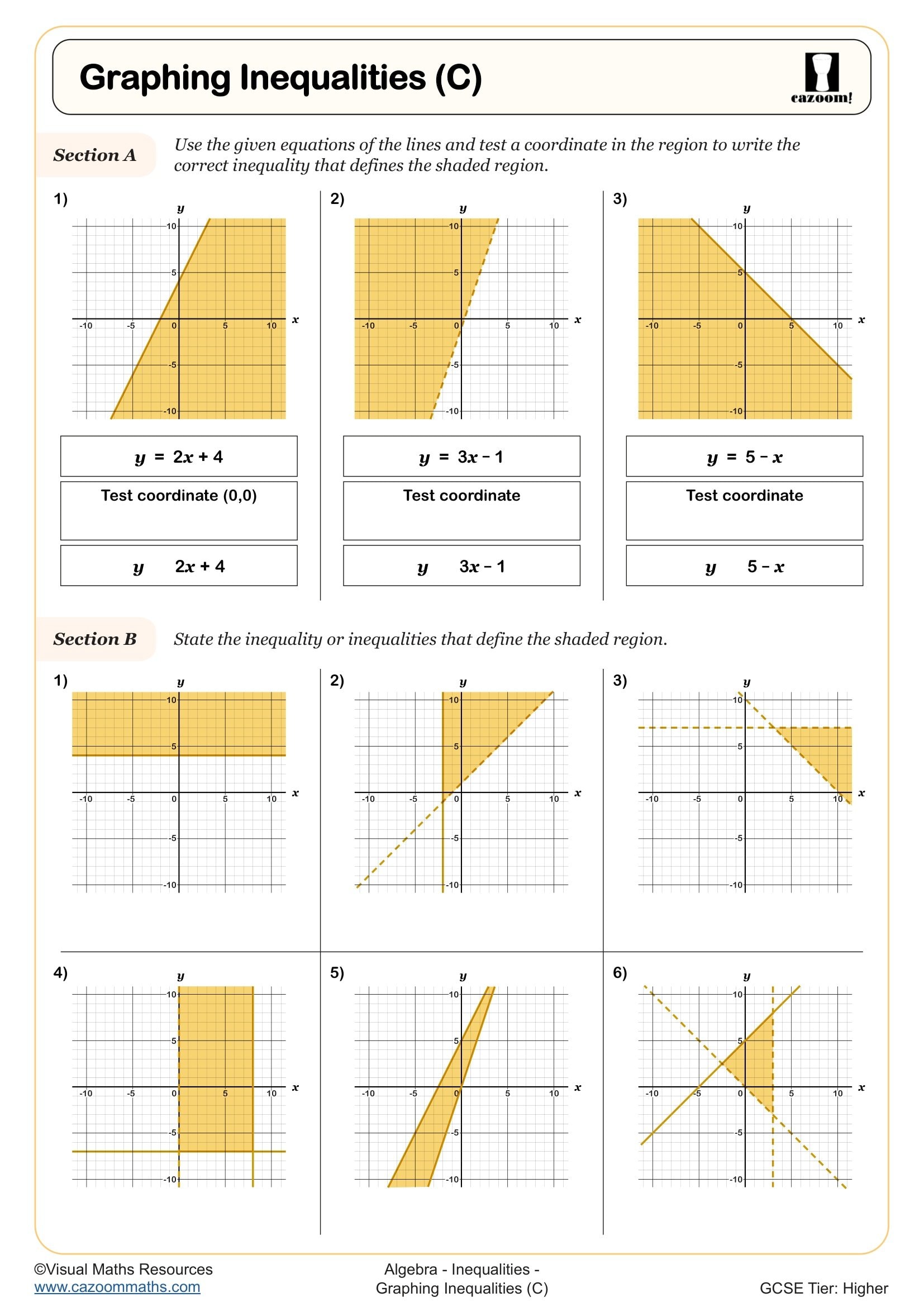
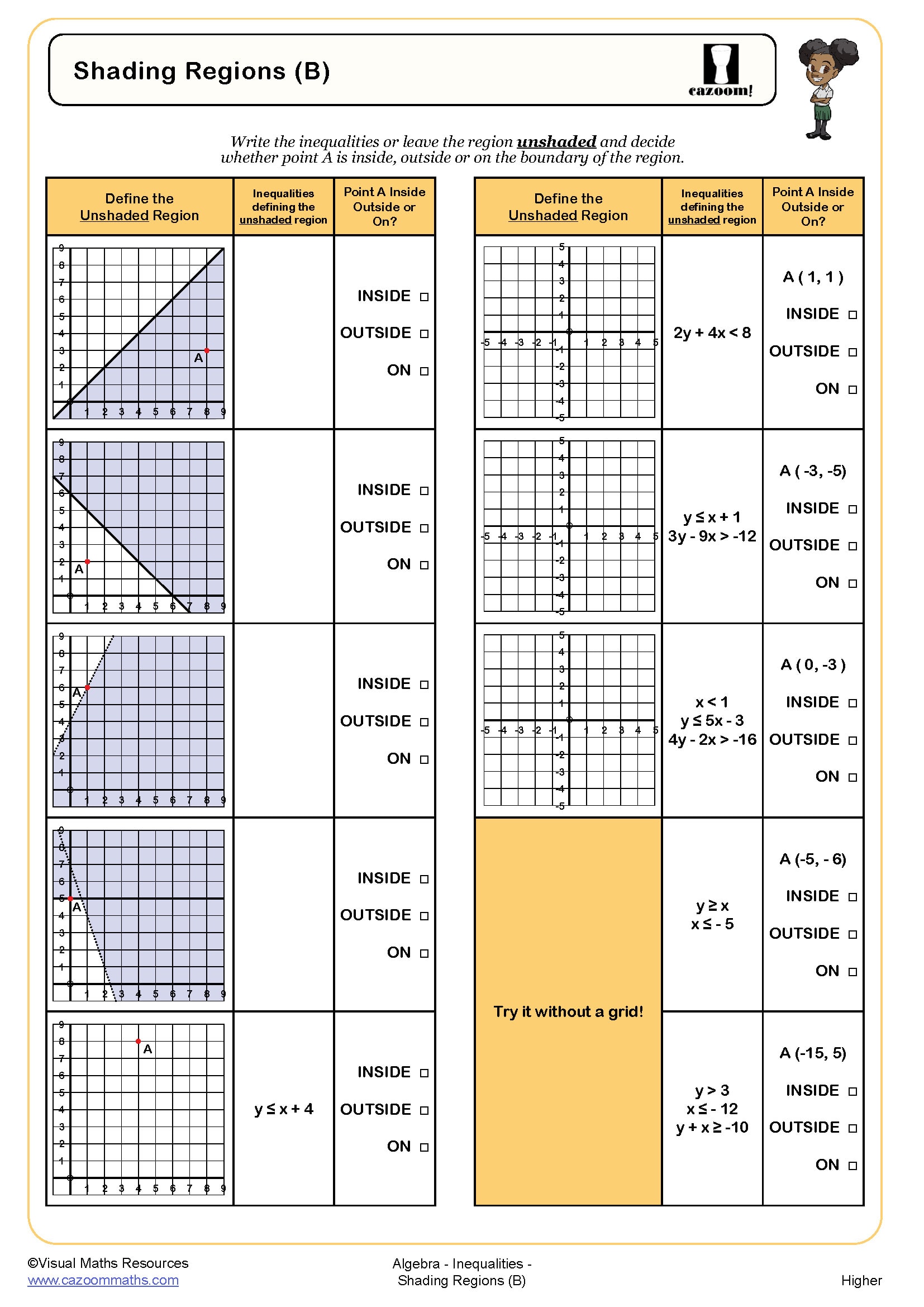
The progression across KS4 moves from solving single linear inequalities and representing solutions on number lines in Year 10, to handling simultaneous inequalities and finding integer solutions that satisfy multiple conditions in Year 11. Higher tier students also encounter quadratic inequalities and graphical representations involving regions, though the focus in these worksheets remains on building solid foundations with linear forms. This scaffolded approach ensures students are prepared for the range of inequality questions that appear across both GCSE papers.
How do you solve two inequalities simultaneously?
When solving two inequalities together, students need to solve each inequality separately first, then identify values that satisfy both conditions. For instance, with 2x + 3 < 11 and x - 1 ≥ 2, students would find x < 4 from the first and x ≥ 3 from the second, concluding that 3 ≤ x < 4. The key skill is combining the two solution sets correctly, which requires careful attention to whether boundaries are included or excluded.
This skill has direct applications in constraint-based problems across science and engineering. Manufacturing processes often require measurements to fall within acceptable tolerances (temperature must exceed 80°C but stay below 120°C), while dose calculations in medicine specify minimum effective amounts and maximum safe limits. Understanding how to express and work with these boundary conditions mathematically develops logical reasoning that extends well beyond GCSE maths into practical STEM contexts where operating within specified ranges is fundamental.
How can teachers use these inequality worksheets effectively?
The worksheets provide structured practice that builds from solving linear inequalities through to satisfying multiple conditions, allowing teachers to target specific skills where students need reinforcement. The included answer sheets enable students to self-check their working, which is particularly valuable for identifying whether errors occur in the algebraic manipulation stage or in the interpretation and notation of solutions.
Many teachers use these resources for differentiated homework, assigning different subtopic worksheets based on diagnostic assessment results from classwork. They also work well for intervention sessions where small groups tackle common misconceptions, such as the sign-reversal rule, with immediate access to fully worked solutions. In revision periods before mock or GCSE exams, students can work through worksheets independently to refresh their understanding of inequality notation and solution methods, building confidence with a topic that often appears as both standalone questions and within problem-solving contexts.