KS4 Non-linear Graphs Worksheets
What Are Non-Linear Graphs in GCSE Maths?
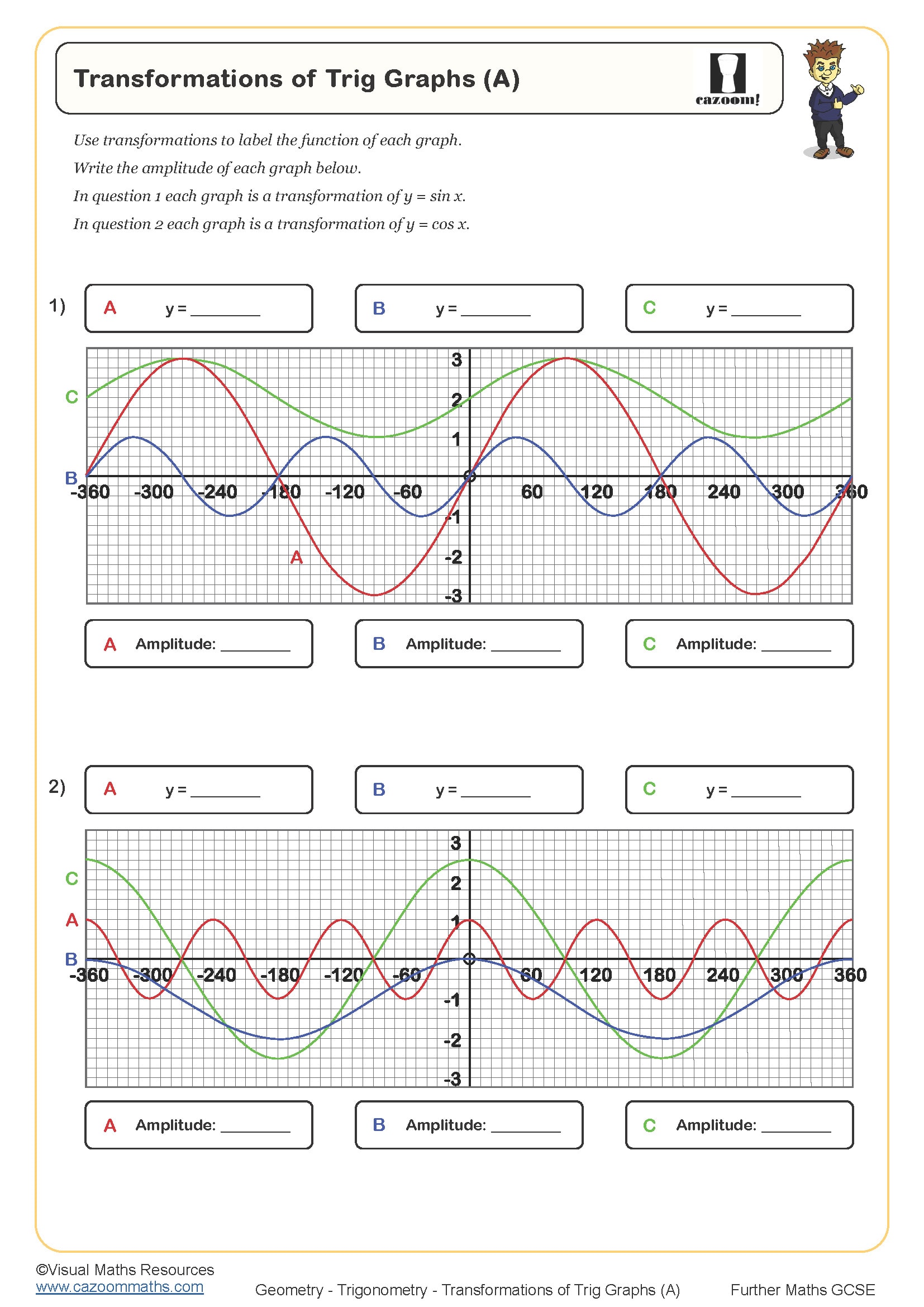
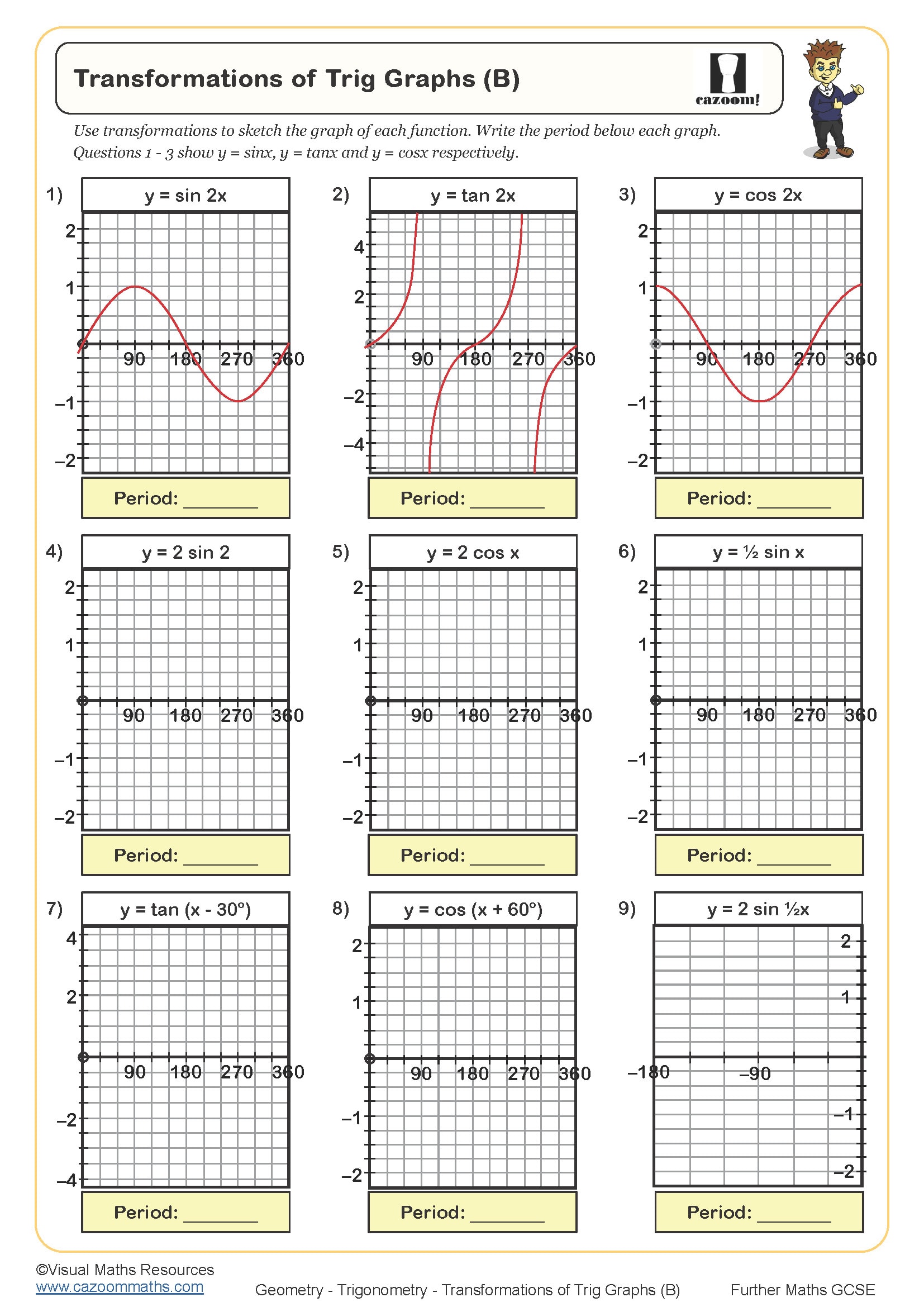
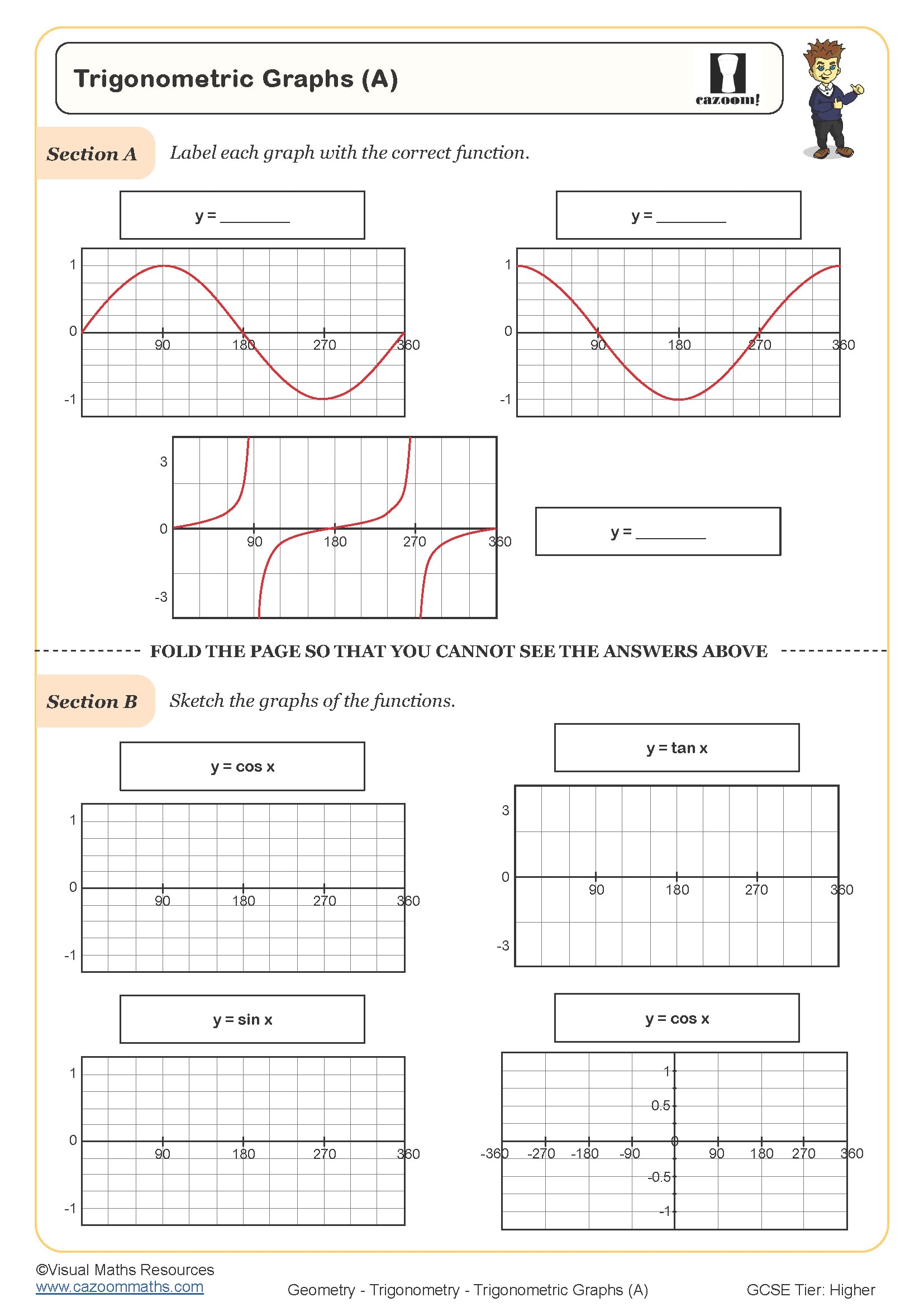
Non-linear graphs represent relationships where the rate of change isn't constant, producing curves rather than straight lines. At GCSE, students work primarily with quadratic graphs (parabolas with equation y = ax² + bx + c), cubic graphs (y = ax³ + bx² + cx + d), and reciprocal graphs (y = k/x). These appear across the higher tier curriculum, from sketching curves using table of values to finding graphical solutions where curves intersect with lines or other curves.
A common error occurs when students plot accurate coordinates but then reach for a ruler, creating angular 'curves' that lose marks in exams. Mark schemes specifically award marks for smooth curves drawn through points, and students need repeated practice recognising the characteristic shapes: quadratics forming U-shapes or inverted U-shapes, cubics with their distinctive S-curve, and reciprocals with two separate branches in opposite quadrants that never touch the axes.
Which Year Groups Study Non-Linear Graphs?
Non-linear graphs feature in the Year 10 and Year 11 curriculum as part of the GCSE higher tier content. Students typically encounter quadratic graphs first in Year 10, building on their understanding of quadratic expressions and equations from earlier in Key Stage 4. By Year 11, the work extends to cubic and reciprocal functions, alongside using graphs to solve equations and inequalities graphically.
The progression across these years moves from plotting points and recognising curve shapes to analysing features like turning points, roots, and asymptotes. Year 10 students might focus on drawing y = x² + 3x - 4 from a table of values, whilst Year 11 work includes identifying that a cubic graph must cross the x-axis at least once (since cubic equations always have at least one real root) and understanding why reciprocal graphs approach but never reach the axes, introducing the concept of asymptotes that becomes important in further mathematics.
How Do You Find Turning Points on Quadratic Graphs?
The turning point (or vertex) of a quadratic graph represents the minimum or maximum value of the function, occurring where the curve changes direction. Students find this by completing the square to write the quadratic in the form y = a(x - h)² + k, where the turning point sits at coordinates (h, k). For example, y = x² - 6x + 11 becomes y = (x - 3)² + 2, revealing the minimum point at (3, 2). Alternatively, the x-coordinate of the turning point lies at x = -b/2a when the quadratic is written as y = ax² + bx + c.
This skill connects directly to optimisation problems across physics and engineering. When calculating the maximum height of a projectile, the trajectory follows a parabolic path where the turning point represents the peak of the flight. Similarly, businesses use quadratic models to find profit-maximising prices, where the turning point indicates the optimal price point between charging too little (low profit per item) and too much (fewer sales), demonstrating why understanding parabola features matters beyond the maths classroom.
How Should Teachers Use These Non-Linear Graphs Worksheets?
The worksheets build skills systematically, starting with plotting curves from given coordinate pairs before progressing to generating tables of values, identifying key features, and solving problems graphically. Each sheet provides opportunities for students to practise the curve-drawing technique that examiners expect, whilst answer sheets allow immediate feedback on whether plotted points are accurate and curves follow the correct shape. This self-checking proves particularly valuable when students work independently on graph sketching, a skill that requires visual feedback to improve.
Many teachers use these resources during intervention sessions with students who score well on algebraic manipulation but lose marks on graphical questions, or as targeted homework before mock examinations. The worksheets also work effectively in paired activities where one student plots a curve whilst their partner checks coordinates against the answer sheet, encouraging discussion about curve smoothness and shape. For revision, students benefit from completing one worksheet per function type (quadratic, cubic, reciprocal) to consolidate their recognition of characteristic features before tackling mixed-graph papers.