KS4 Percentages Worksheets
Compound Interest
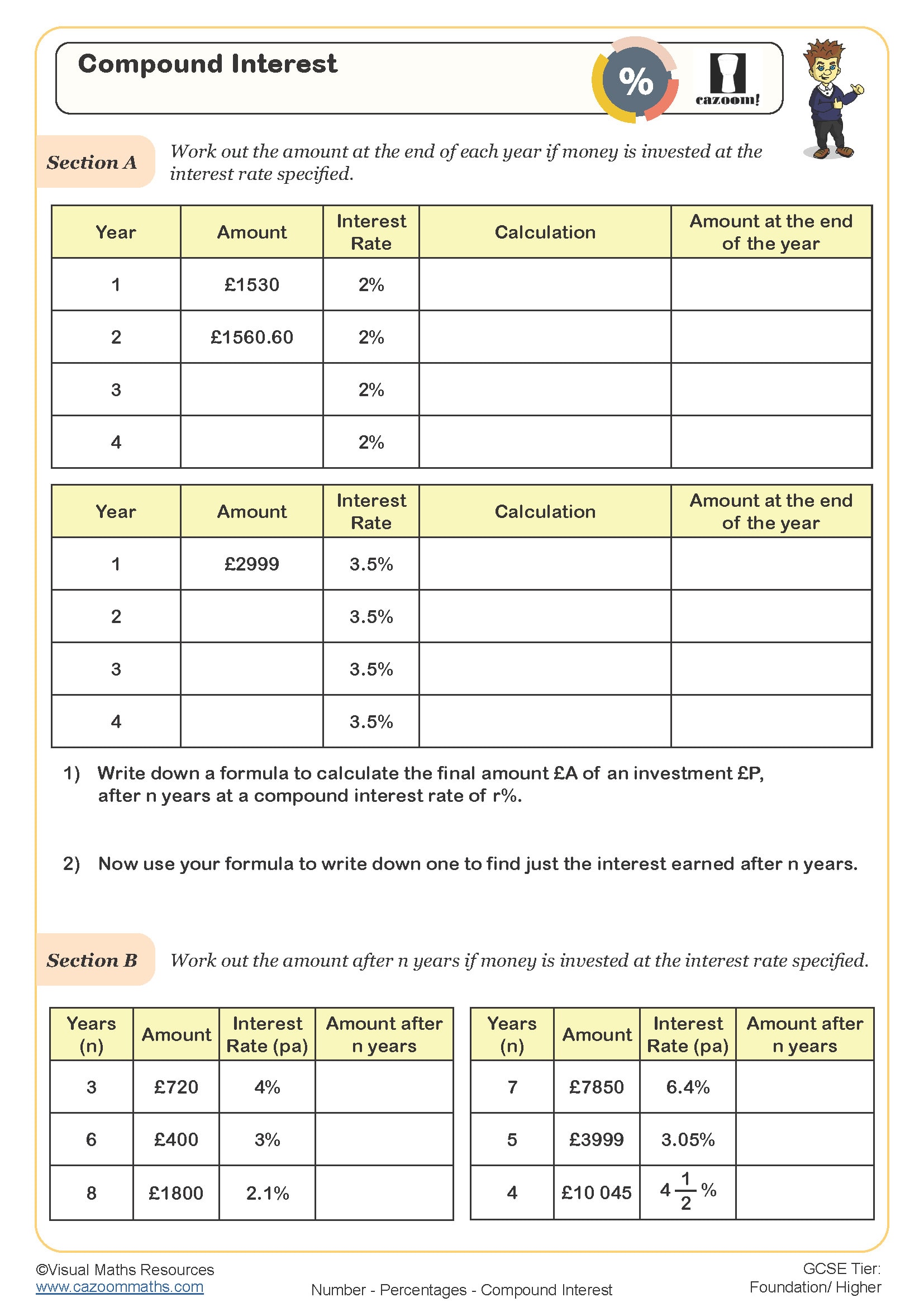
Compound Interest - Problem Solving

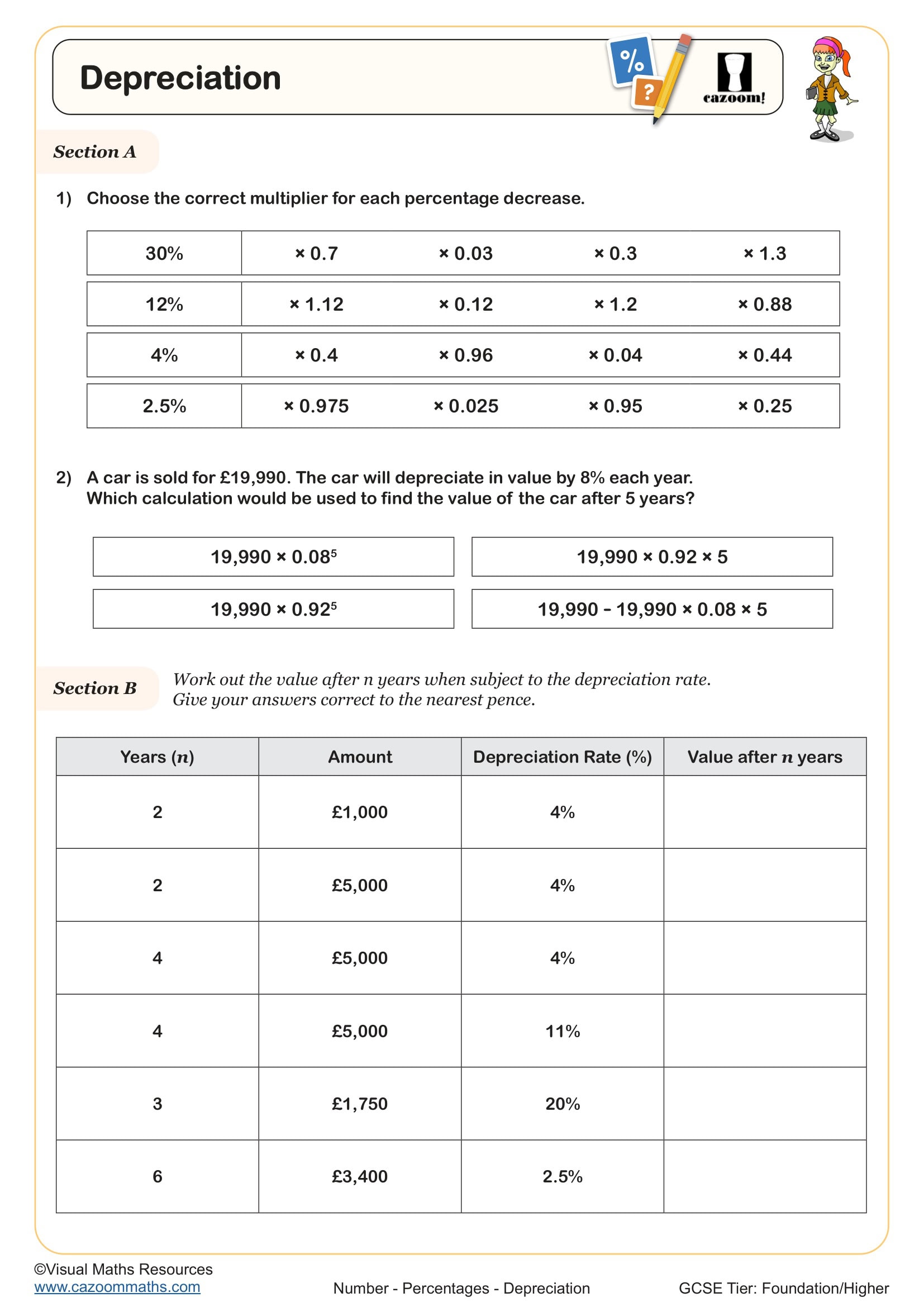
Depreciation
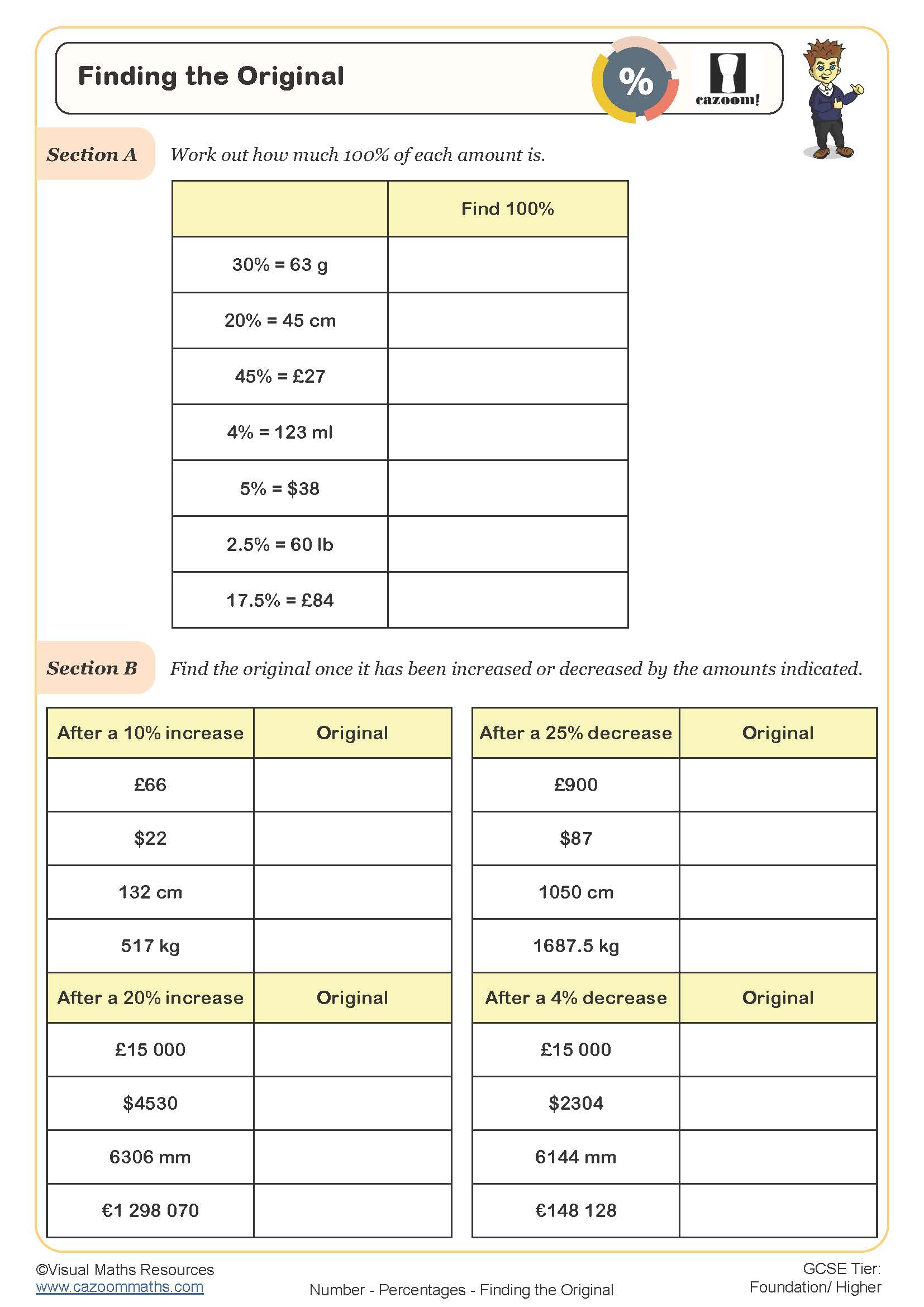
Finding the Original
Fraction, Percentage and Ratio Problems

Interest Comparisons

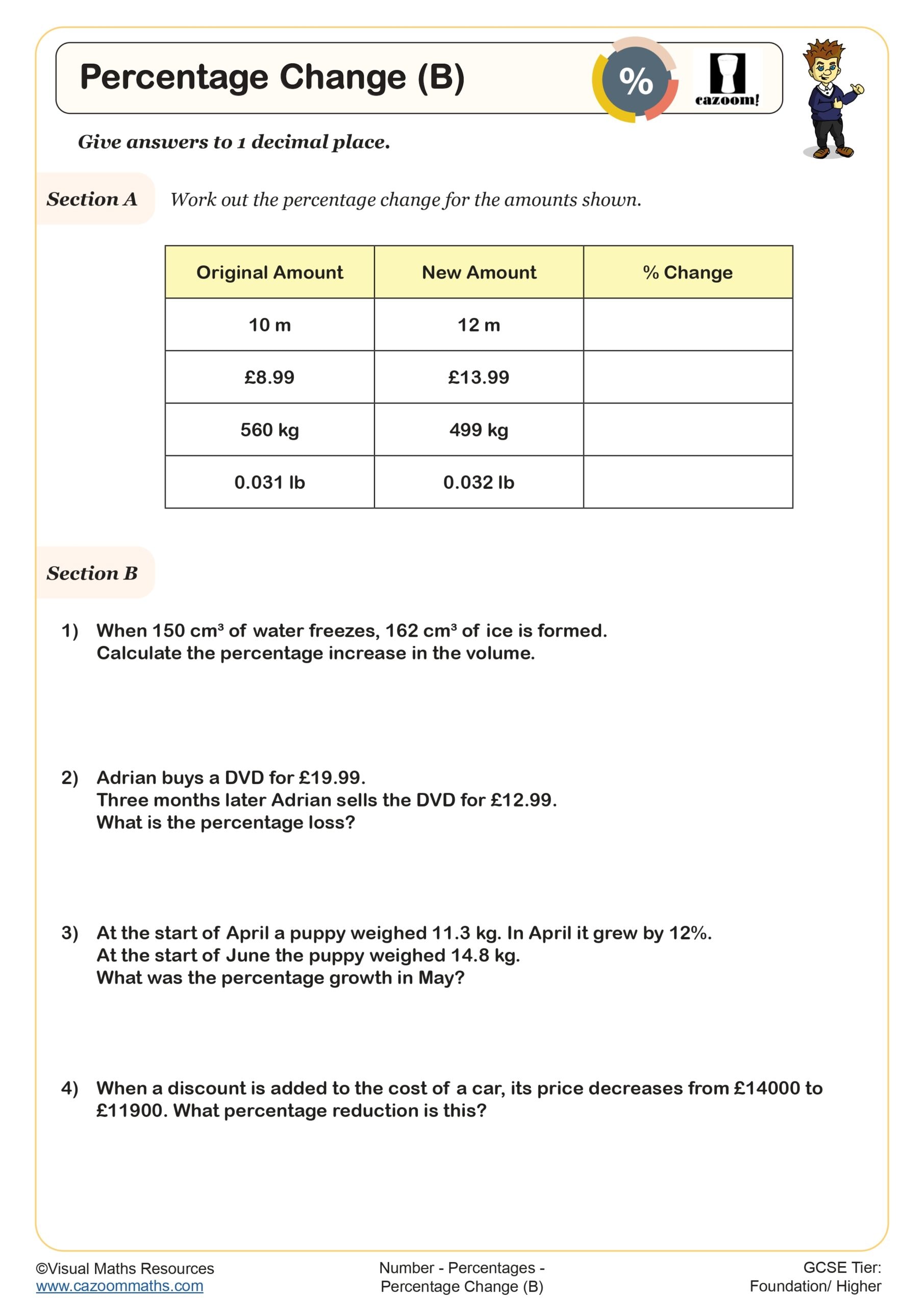
Percentage Change (B)
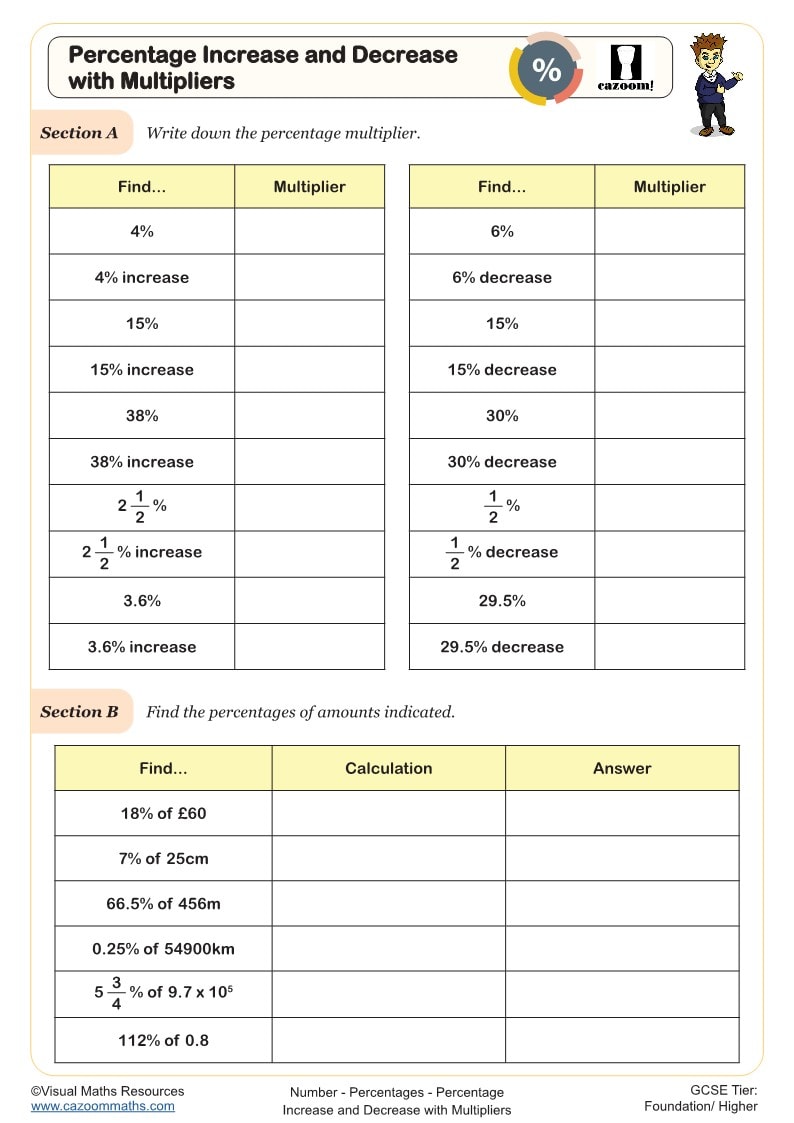
Percentage Increase and Decrease with Multipliers
Percentage Problems

Reverse Percentages - Using a Bar Model (A)

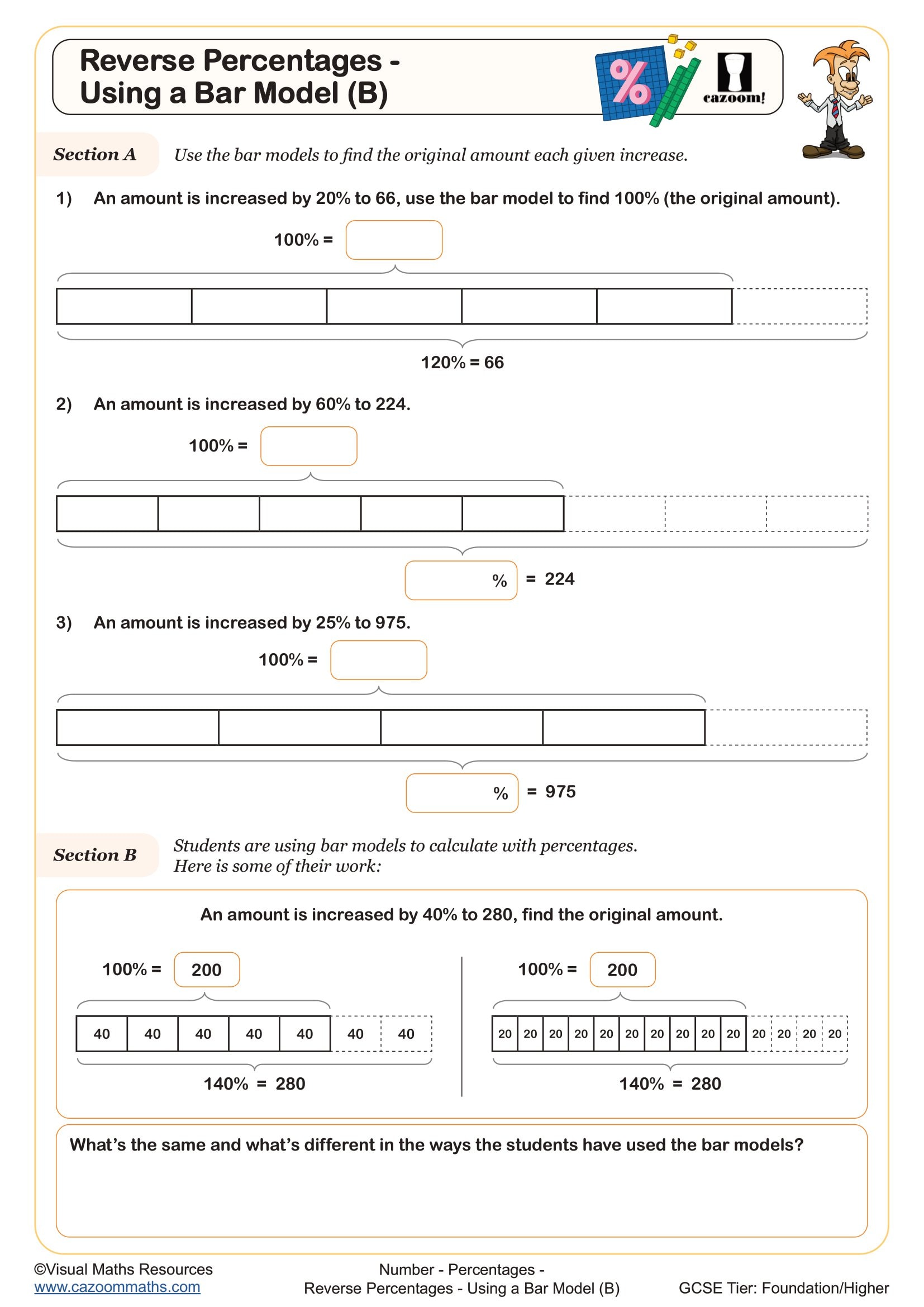
Reverse Percentages - Using a Bar Model (B)
What should percentage worksheets include for KS4 students?
Effective percent worksheets for Key Stage 4 need to cover finding percentages of amounts, percentage increase and decrease, expressing one value as a percentage of another, and reverse percentages. At GCSE level, these skills appear across both Foundation and Higher papers, often embedded within functional questions about finance, data analysis, or measurement contexts.
Teachers frequently notice that students struggle most with reverse percentages, where they need to work backwards from an increased or decreased amount. A typical error involves dividing by the percentage rather than by the decimal multiplier. For example, when an item costs £84 after a 20% increase, students might incorrectly divide by 20 instead of by 1.2 to find the original price. Regular practise with structured percents worksheets helps students recognise which operation the question demands.
Which year groups study percentages at KS4?
At Key Stage 4, percentages form part of the Number strand for both Year 10 and Year 11 students. The topic builds on percentage work from KS3, where students developed fluency with finding percentages of amounts and simple percentage changes. By KS4, students tackle more complex applications including compound percentage changes and financial mathematics.
The progression across Years 10 and 11 typically moves from straightforward percentage calculations towards multi-step problems and reverse percentages. Year 10 students consolidate percentage increase and decrease with single multipliers, whilst Year 11 revision often focuses on exam-style questions combining percentages with ratio, algebra, or data interpretation. Higher tier students also work with repeated percentage change and growth/decay problems that connect to exponential functions.
Why do students need to practise using 25% and 50% in calculations?
Working with 25 and 50 percent provides students with efficient calculation strategies that save time in exams. Recognising that 25% means dividing by 4 and 50% means halving allows for quick mental arithmetic without calculators. These benchmark percentages also help students estimate answers and check whether their calculated results make sense, a skill that examiners value when awarding method marks.
These percentages appear frequently in real-world contexts including VAT calculations (20%), discount rates (25% off, 50% sale), and deposit requirements (typically 10% or 25%). In STEM fields, percentage concentrations in chemistry often use 25% or 50% solutions, whilst data scientists regularly work with quartiles representing 25%, 50%, and 75% of datasets. Understanding these common percentages builds numerical fluency that extends beyond mathematics into science, business studies, and everyday financial decisions.
How do these worksheets help students prepare for GCSE percentages questions?
The worksheets provide structured progression through percentage skills with questions that mirror GCSE paper layouts and mark scheme expectations. Students encounter a range of problem types, from straightforward calculations worth 1-2 marks to multi-step functional questions worth 4-5 marks. Having complete answer sheets allows students to identify exactly where their method breaks down, particularly useful for complex percentage change problems where partial credit depends on correct intermediate steps.
Teachers use these resources effectively for differentiated intervention, assigning specific worksheets to address gaps identified through assessment. They work well for paired practice where stronger students explain their methods, reinforcing understanding for both partners. Many teachers set targeted percentage practice as homework before mock exams, using the answer sheets for students to self-mark and flag specific question types for classroom discussion. The worksheets also support retrieval practice, with teachers revisiting percentage skills regularly throughout Years 10 and 11 to maintain fluency.