KS4 Similarity and Congruence Worksheets
What is the difference between similarity and congruence in GCSE maths?
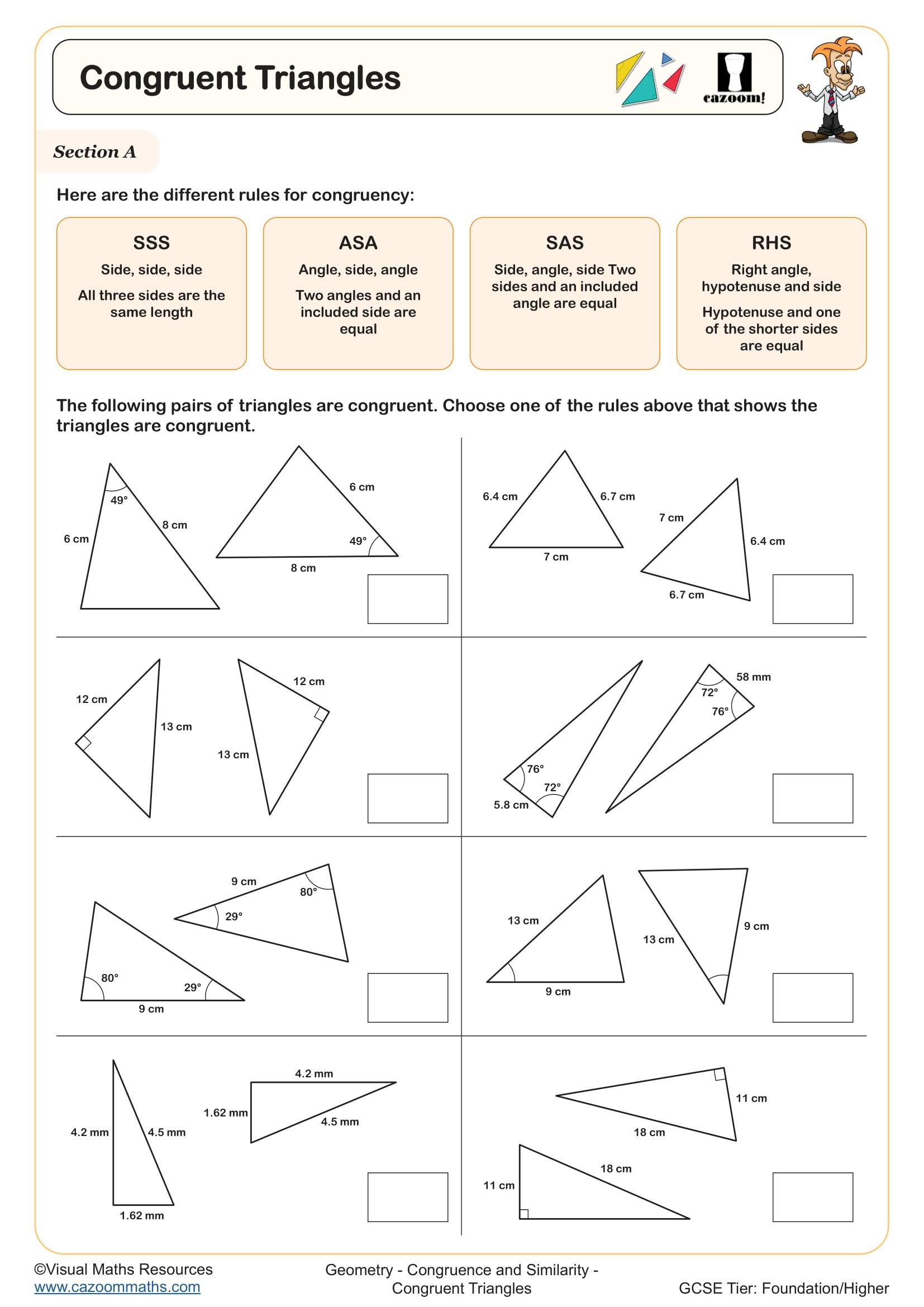
Congruent shapes are identical in both size and shape, meaning all corresponding sides and angles match exactly. Similar shapes have the same angles and proportional sides, but different sizes, connected by a scale factor. Students must prove congruence using four conditions: SSS (three sides equal), SAS (two sides and included angle), ASA (two angles and included side), or RHS (right angle, hypotenuse and one side for right-angled triangles).
A common error occurs when students claim shapes are congruent simply because they look the same, without verifying measurements or applying formal proof methods. Exam questions frequently ask candidates to state which congruence condition they've used, and marks are lost when students write 'they're the same' instead of citing SSS, SAS, ASA or RHS. Teachers report that students often muddle the order of letters in congruence statements, writing triangle ABC is congruent to triangle XZY when corresponding vertices don't match, which loses marks in formal proof questions.
Which year groups study similarity and congruence?
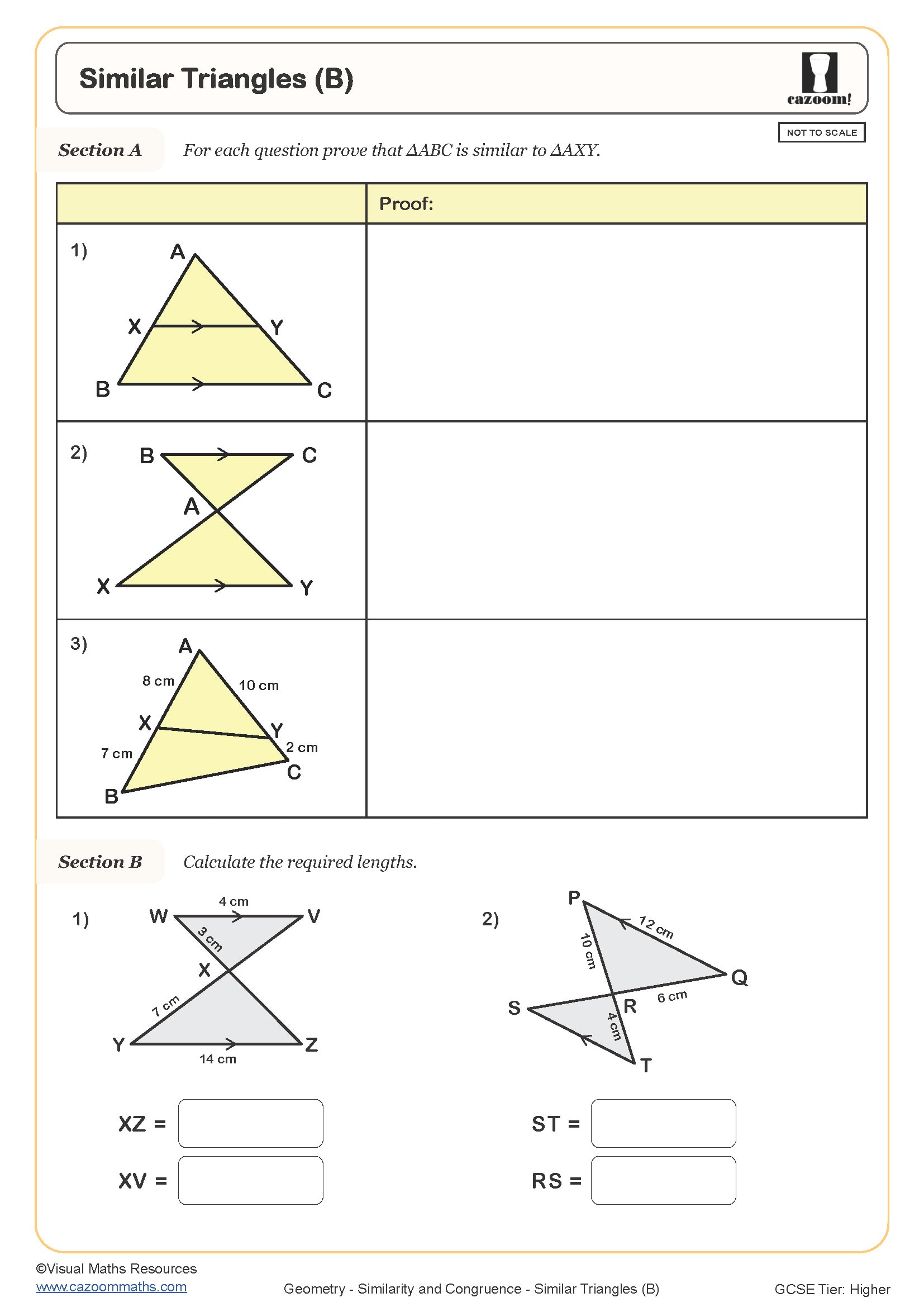
Similarity and congruence worksheets target Year 10 and Year 11 students following the GCSE curriculum. The topic appears in both Foundation and Higher tier papers, though Higher tier includes more demanding questions on area and volume scale factors, combined transformations, and algebraic proofs. Students encounter basic congruence in Year 9 when studying transformations, but formal proof methods and similarity ratios form part of the KS4 programme of study.
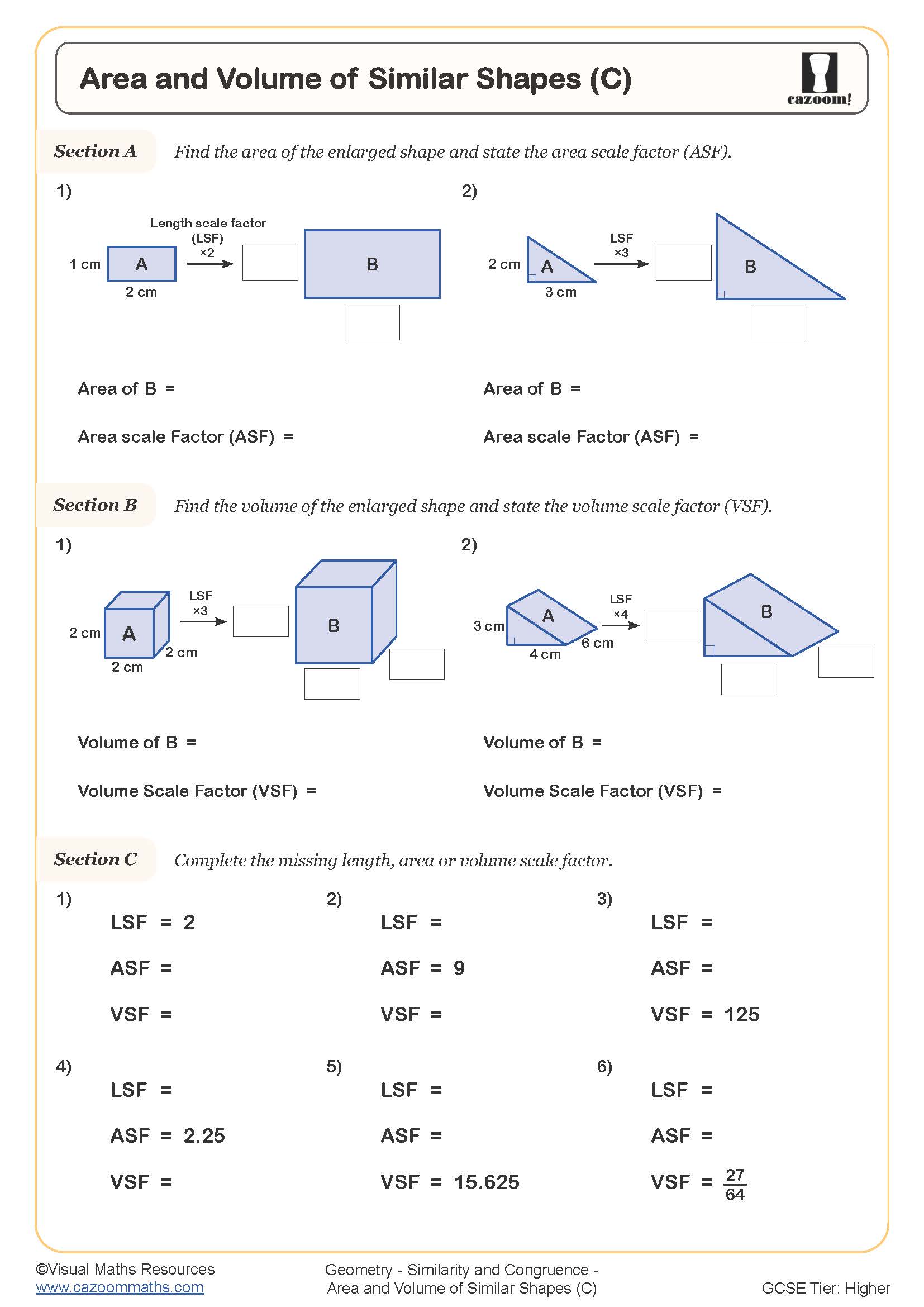
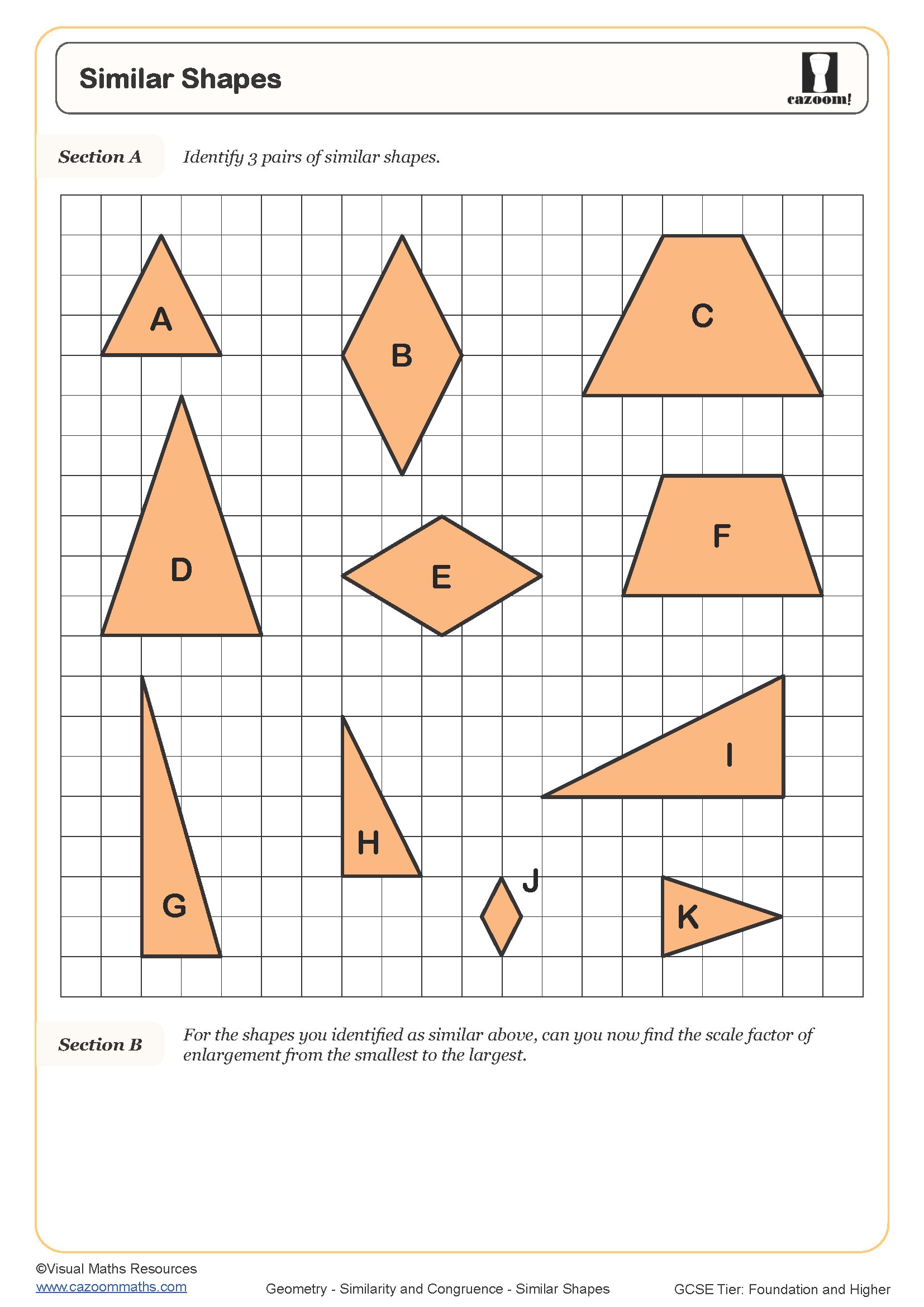
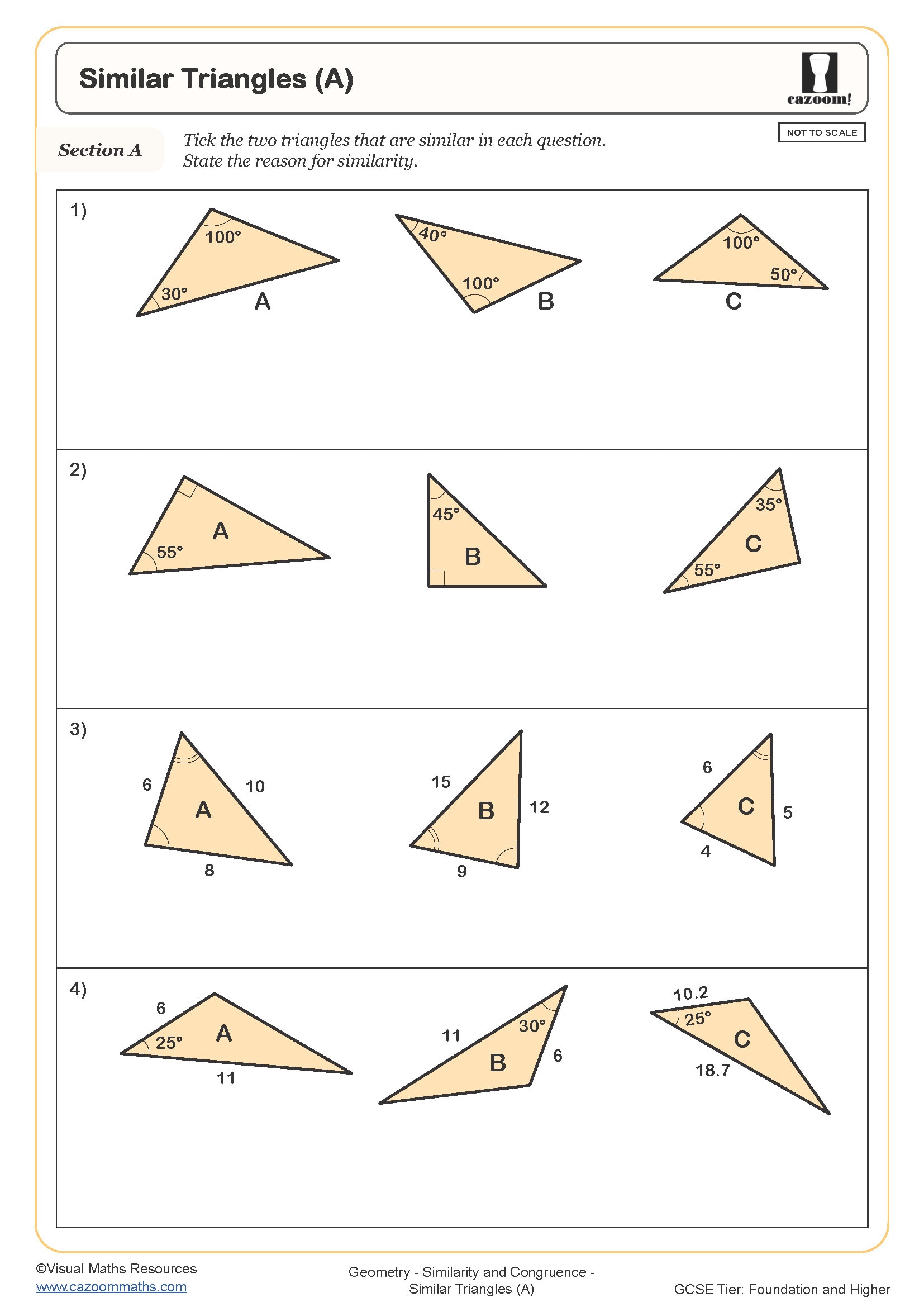
The difficulty increases substantially from Year 10 to Year 11, with early worksheets focusing on identifying similar triangles and calculating missing lengths using scale factors. By Year 11, students tackle questions involving area ratios (scale factor squared) and volume ratios (scale factor cubed), plus multi-step problems where they must find a scale factor before calculating an unknown measurement. Higher tier students also work with algebraic expressions in similarity questions, setting up and solving equations to find dimensions.
How do you calculate area and volume scale factors?
When two shapes are similar with a linear scale factor of k, the area scale factor equals k² and the volume scale factor equals k³. This relationship catches many students out because they apply the linear scale factor directly to areas and volumes, leading to incorrect answers that are too small. For example, if a triangle enlarges by scale factor 3, its area multiplies by 9, not 3. Students must identify the type of measurement (length, area, or volume) before applying the appropriate scale factor.
Architects and engineers use these principles constantly when creating scale models of buildings or prototypes of vehicles. A 1:50 architectural model doesn't just have dimensions 50 times smaller; its surface area is 2,500 times smaller and its volume 125,000 times smaller, which matters when calculating material costs or structural loads. Medical researchers apply volume scale factors when dosing medications based on body mass, since drug requirements scale with volume rather than linear dimensions, making this concept crucial in pharmaceutical calculations.
How do these worksheets help students prepare for GCSE exams?
The worksheets build fluency through structured practise, starting with recognition tasks where students identify similar or congruent shapes, then progressing to calculation questions requiring scale factor applications. Each worksheet includes worked examples showing the method step-by-step, which helps students who struggle to know where to start when faced with unfamiliar diagram layouts. The answer sheets allow students to self-assess their understanding and identify whether errors stem from misreading the scale factor, applying the wrong condition, or making calculation mistakes.
Teachers use these resources for targeted intervention with students who lose marks on transformation geometry, as homework to reinforce classroom teaching, or as revision material before mock exams. The worksheets work well for paired work, with one student completing even-numbered questions while their partner tackles odd-numbered ones, then comparing methods and answers. Many teachers set particular worksheets as timed practise to help students develop exam pace, since GCSE papers typically allocate only two to three minutes per similarity or congruence question.