Direct and Inverse Proportion Relationships Worksheets
All worksheets are created by the team of experienced teachers at Cazoom Maths.
What is the difference between direct and inverse proportion?
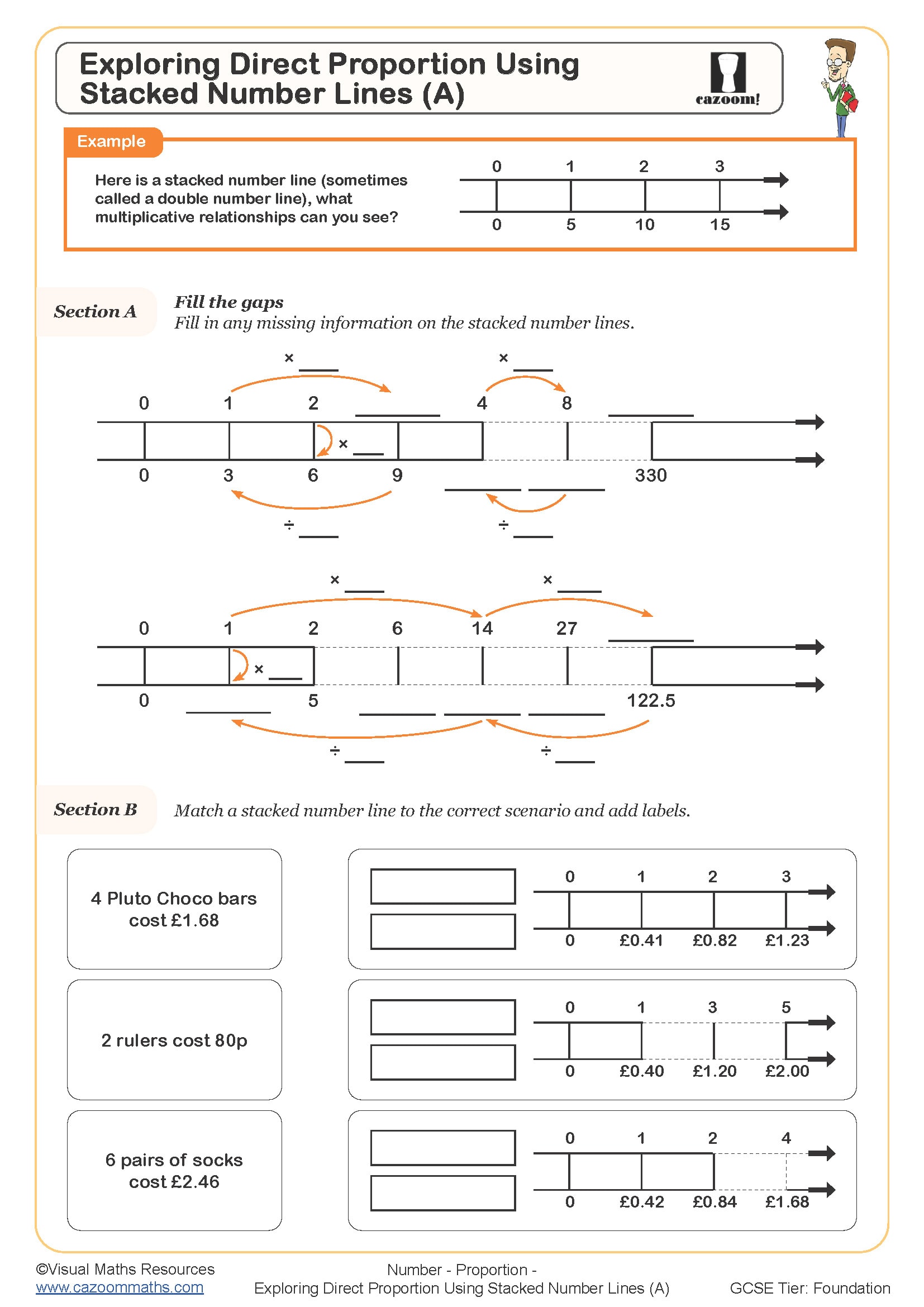
Direct proportion exists when two quantities increase or decrease at the same rate, so if one doubles, the other doubles. Inverse proportion occurs when one quantity increases while the other decreases proportionally, meaning if one doubles, the other halves. Students encounter direct proportion in contexts like recipe scaling or currency conversion, whilst inverse proportion appears in situations like journey time versus speed.
A common error teachers observe is students applying direct proportion methods to inverse problems. For instance, when presented with 'If 6 workers complete a job in 8 hours, how long will 12 workers take?', students often double the time instead of halving it. Recognising the relationship type before calculating is essential, yet many lose marks by rushing into calculations without identifying whether more of one quantity leads to more or less of the other.
Which year groups study direct and inverse proportion?
These worksheets cover Year 7, Year 8, Year 9, and Year 10, spanning both Key Stage 3 and Key Stage 4. Direct proportion typically appears first in Year 7 as an extension of ratio work, whilst inverse proportion is usually introduced in Year 8 or Year 9, depending on student readiness. The National Curriculum expects students to solve problems involving both types by the end of KS3.
Progression moves from simple direct proportion with whole numbers in Year 7 to more complex scenarios involving decimals and fractions. Year 9 and Year 10 worksheets incorporate algebraic notation (y ∝ x and y ∝ 1/x), graphical representations, and exam-style questions that combine both relationship types. Higher tier GCSE students must also work with proportion constants and square or cube proportion relationships, which build on these foundational skills.
How do you solve inverse proportion problems using the constant method?
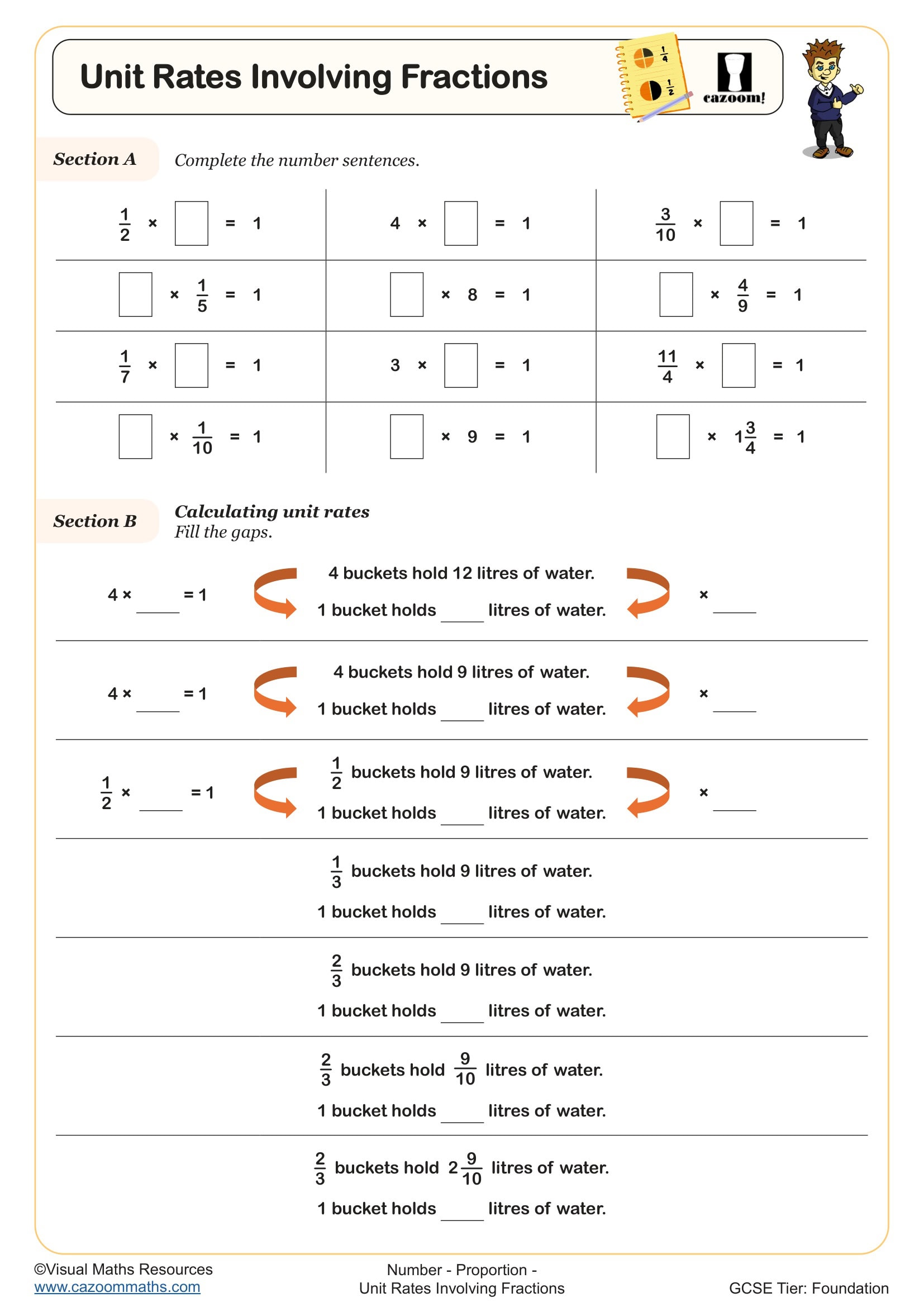
The constant method uses the principle that for inversely proportional quantities, their product remains constant. If x and y are inversely proportional, then x × y = k (a constant value). Students find k using the initial values, then use this constant with the new value to calculate the unknown. For example, if 5 workers take 12 days (5 × 12 = 60), then for 10 workers, 10 × days = 60, so days = 6.
This concept connects directly to real-world contexts in engineering and economics. Manufacturing processes use inverse proportion when calculating production time versus workforce size, whilst fuel consumption relates inversely to vehicle efficiency. Understanding that the product stays constant helps students tackle problems in physics, such as Boyle's Law relating pressure and volume in gases, or calculating gear ratios in mechanical systems where speed and torque are inversely proportional.
How can teachers use these proportion worksheets effectively?
The worksheets scaffold learning through carefully sequenced questions that build from simple recognition tasks to multi-step problem-solving. Answer sheets allow students to self-check their working, which is particularly valuable when developing the systematic methods needed for proportion calculations. Teachers can identify at which stage students make errors, whether in setting up the relationship, finding the constant, or applying it to new values.
Many teachers use these resources for differentiated group work, with earlier year group sheets providing support for students still developing confidence whilst higher year materials challenge stronger students. The worksheets work well as homework following classroom teaching, as retrieval practice in starter activities, or during intervention sessions where students need to revisit proportion before tackling more advanced topics like compound measures or percentage change, both of which rely on proportional reasoning.