Prime Factorisation Worksheets
Investigating Prime Factors
Year groups: 7, 8

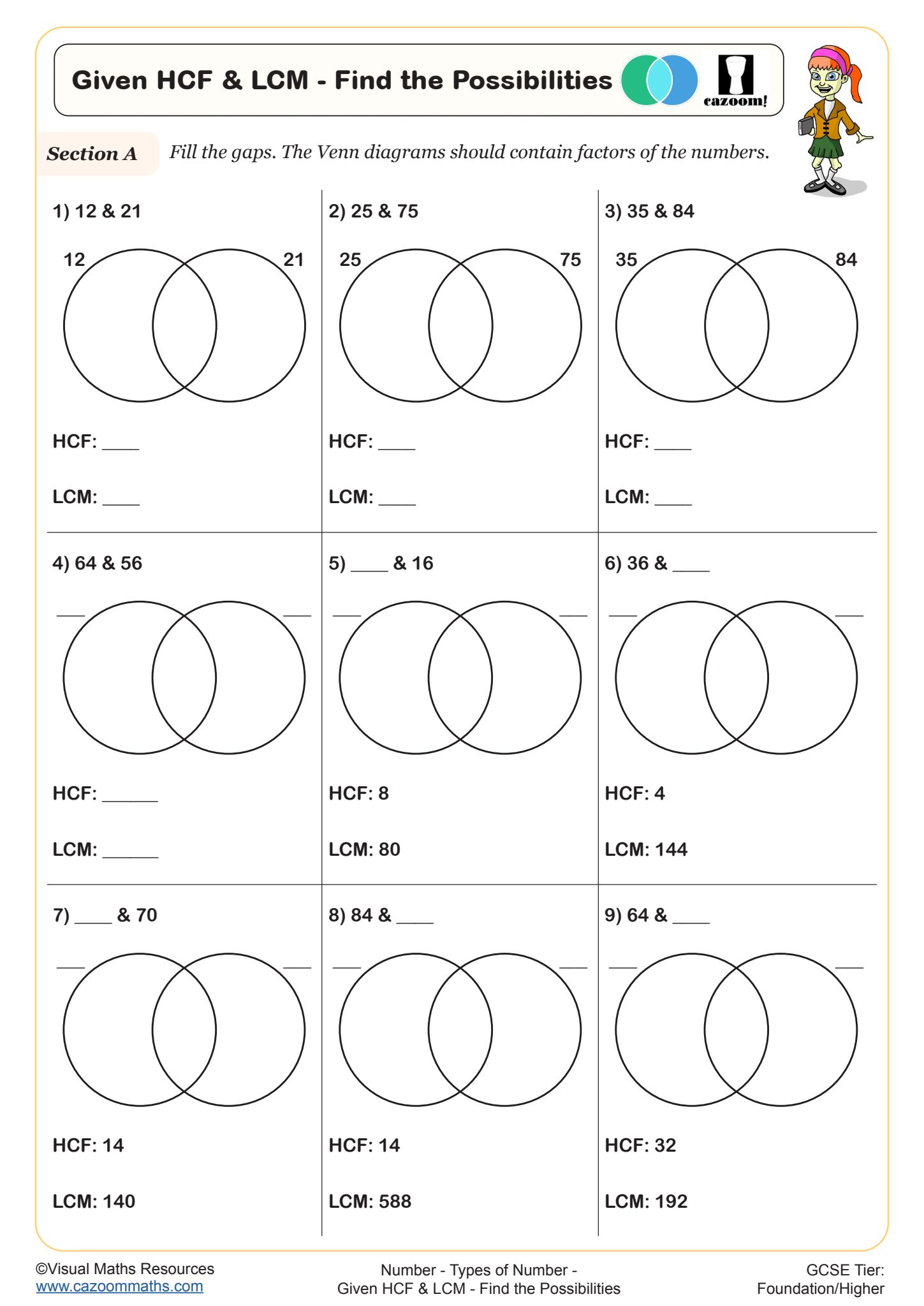
Given HCF & LCM - Find Possible Numbers
Year groups: 8, 9
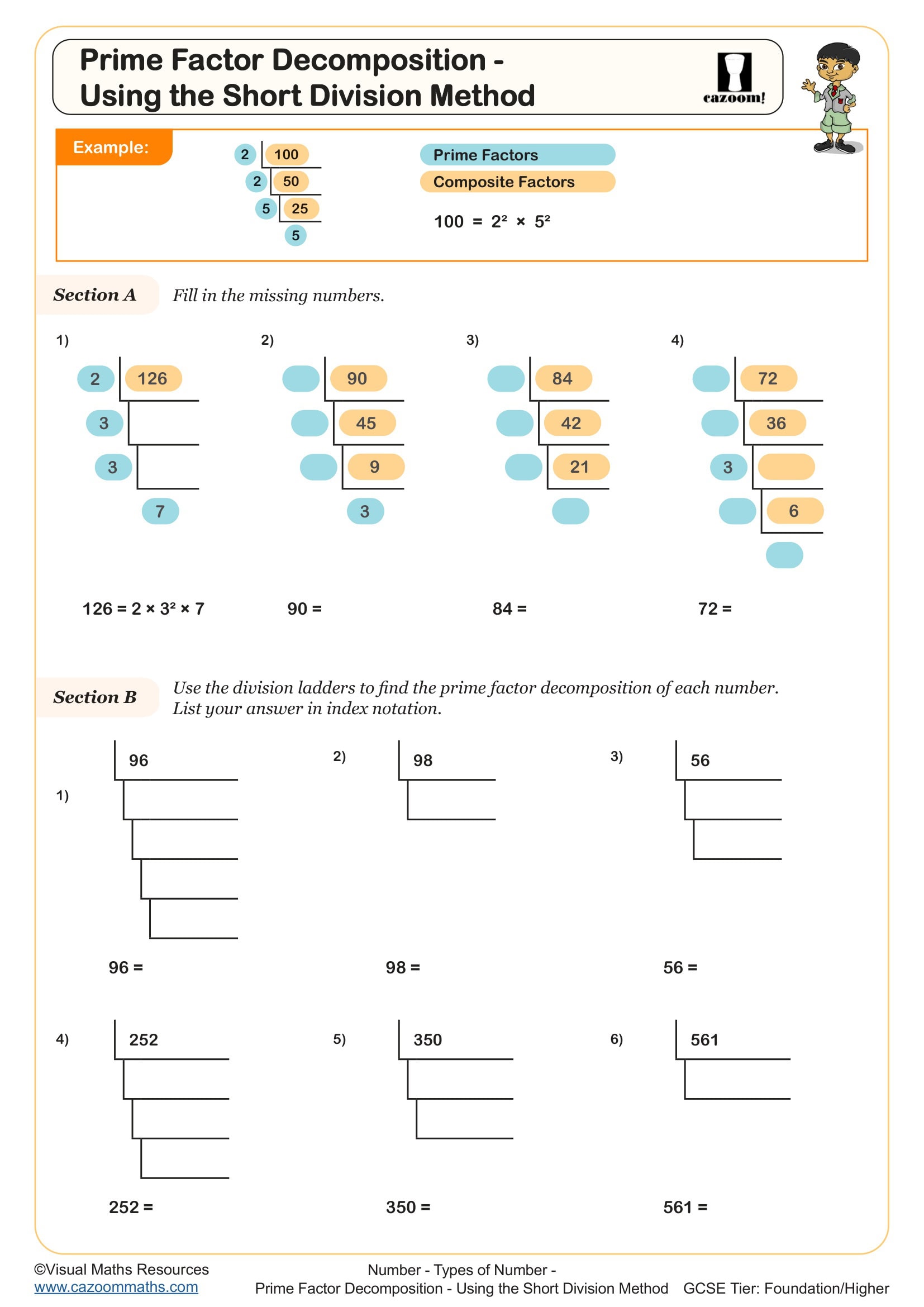
Prime Factor Decomposition - Using the Short Division Method
Year groups: 8, 9
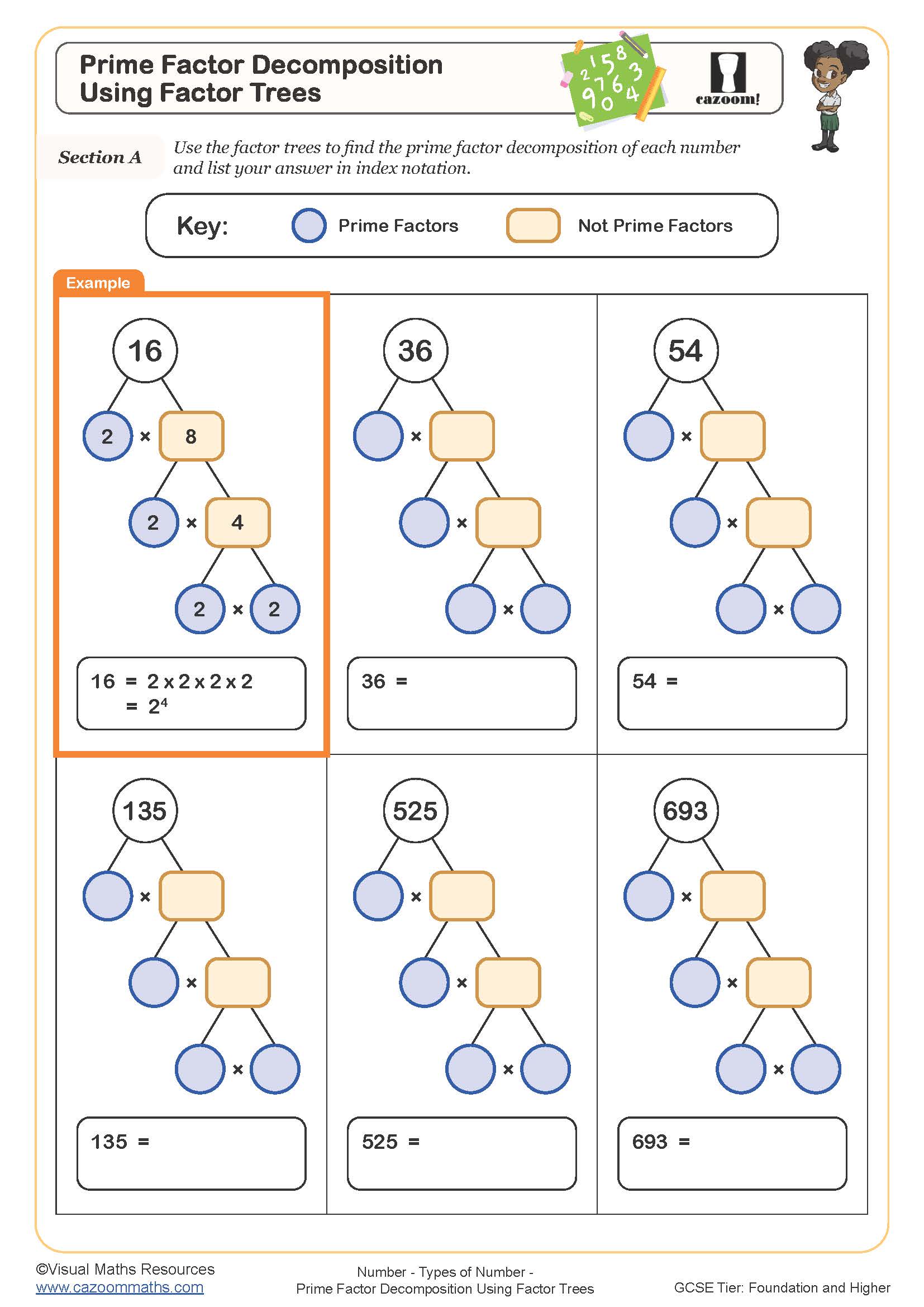
Prime Factor Decomposition Using Factor Trees
Year groups: 8, 9, 10
Using Prime Decomposition to Find HCF and LCM (A)
Year groups: 8, 9, 10

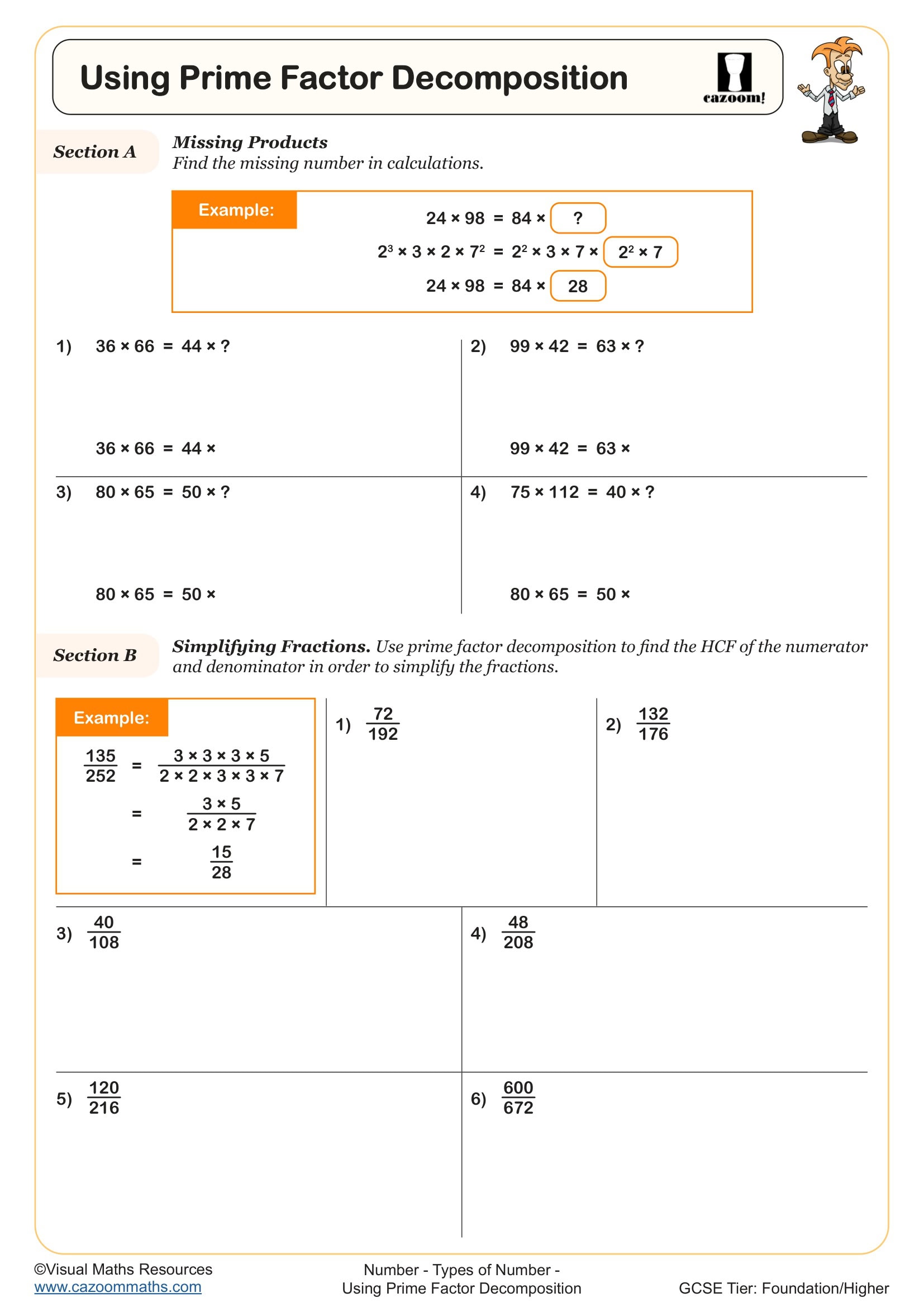
Using Prime Factor Decomposition
Year groups: 8, 9
Using Prime Factors to Identify Square, Cube Numbers and Roots
Year groups: 8, 9

Using Prime Decomposition to Find HCF and LCM (B)
Year groups: 9, 10, 11

All worksheets are created by the team of experienced teachers at Cazoom Maths.
What is a prime factorisation worksheet?
A prime factorisation worksheet provides structured practice in expressing composite numbers as products of prime factors, typically using index notation for repeated factors. These worksheets guide students through methods such as factor trees or the division method, where numbers are systematically divided by prime numbers until only 1 remains. The National Curriculum introduces this at Key Stage 3 as part of number structure and properties, building towards applications in ratio, fractions, and algebraic manipulation.
Students often lose marks on GCSE questions by forgetting to use index form, writing 2 × 2 × 2 × 5 instead of 2³ × 5, even when the question specifically asks for prime factor decomposition in index notation. The division method worksheets particularly help students who struggle with factor trees, offering a more systematic alternative that reduces the chance of missing factors. Each worksheet includes fully worked solutions showing both methods where appropriate.
Which year groups use prime factorisation worksheets?
Prime factorisation worksheets are available for Year 7, Year 8, Year 9, Year 10, and Year 11, spanning both Key Stage 3 and Key Stage 4. The topic typically appears in Year 7 as an introduction to number structure, building on the understanding of factors and multiples from primary school. Students learn to identify prime numbers and express small composite numbers as products of primes, usually starting with numbers under 100.
The difficulty progresses significantly across the year groups. Year 7 and 8 worksheets focus on numbers with obvious prime factors and developing fluency with factor trees, whilst Year 9 onwards introduces three-digit numbers and connections to HCF and LCM problems. By Year 10 and 11, prime factor worksheets link directly to GCSE requirements, including reverse problems where students must find a number from its given prime factor decomposition, such as working out what number has the prime factor decomposition 5² × 71. Higher-tier papers frequently combine prime factorisation with surds or algebraic fractions.
Why do we teach the division method for prime factorisation?
The division method (also called the ladder method or repeated division) provides a systematic approach where students divide by the smallest prime factor repeatedly, recording each prime divisor until reaching 1. Unlike factor trees which can follow different paths, the division method follows one clear sequence, making it particularly useful for students who find the branching structure of trees confusing. Teachers often introduce both methods but find that struggling students benefit from the linear structure of division, as it reduces cognitive load and prevents the common error of including composite factors.
This systematic approach mirrors computational thinking in computer science, where algorithms break complex problems into repeated simple operations. Cryptography, which secures online banking and digital communications, relies entirely on the difficulty of prime factorisation for very large numbers—whilst students work with manageable numbers like 360 or 504, the same principle protects data when applied to numbers with hundreds of digits. Understanding that every composite number has exactly one unique prime factorisation (the Fundamental Theorem of Arithmetic) connects school mathematics to real-world security systems.
How do these worksheets help students improve at prime factorisation?
The worksheets build confidence through carefully graduated questions, starting with numbers that have obvious prime factors (like multiples of 10 or 12) before progressing to less familiar composites. Many include worked examples demonstrating both factor tree and division methods side-by-side, helping students choose the approach that suits their thinking. The answer sheets show complete working, not just final answers, which proves particularly valuable when students get partway through a factor tree and lose track of which branches they've completed.
Teachers use these resources flexibly across different classroom contexts. They work well for homework when introducing the topic, as students can attempt questions then check their method against the answers before the next lesson. In intervention sessions, the worksheets help identify whether errors stem from not recognising prime numbers or from organisational issues with recording factors. Paired work often reveals interesting discussions when students compare different factor tree routes to the same answer, reinforcing that whilst the tree structure varies, the final prime factorisation remains unique.