Square and Cube Numbers Worksheets
All worksheets are created by the team of experienced teachers at Cazoom Maths.
What are square and cube numbers?
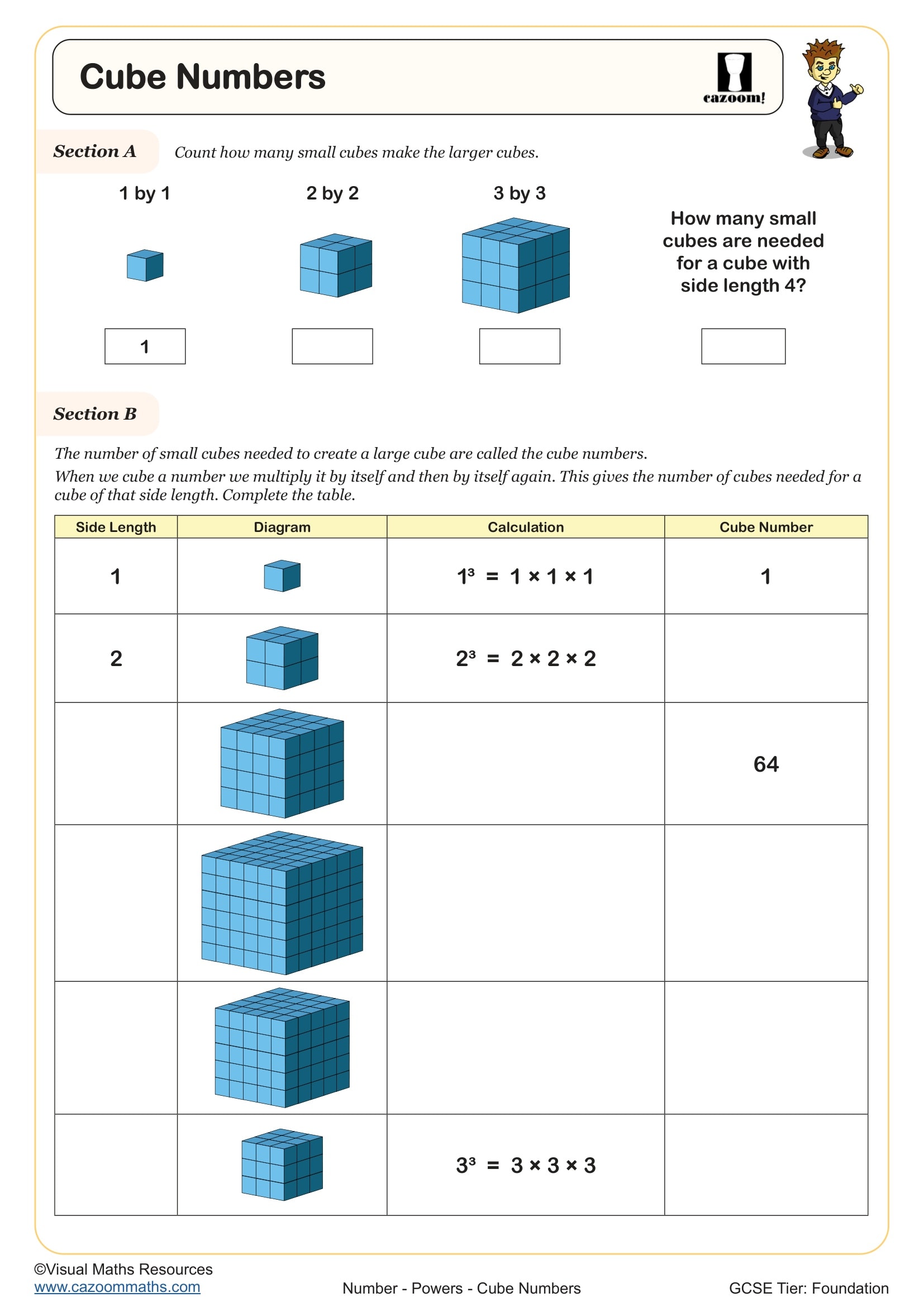
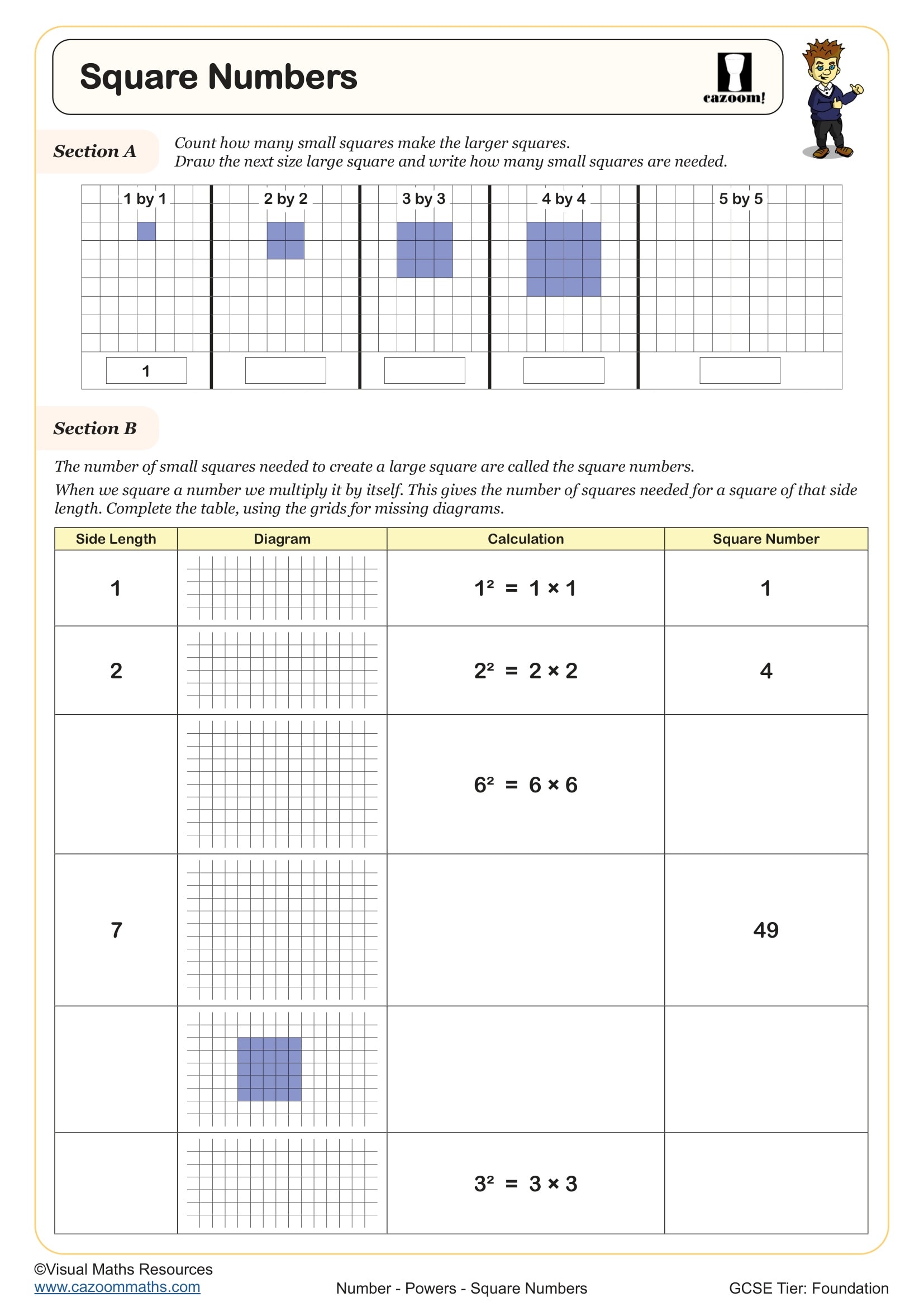
Square numbers result from multiplying any whole number by itself (n × n or n²), such as 4, 9, 16, 25, while cube numbers come from multiplying a number by itself twice (n × n × n or n³), giving values like 8, 27, 64, 125. Students meet these concepts formally in Year 7 as part of the National Curriculum's requirements for understanding powers and roots, which underpin algebraic manipulation and problem-solving throughout secondary mathematics.
A common error occurs when students calculate 5³ as 15 (confusing multiplication with addition) rather than 125. Teachers often use visual representations—grids for squares and stacked cubes for cube numbers—to reinforce why the terminology makes sense geometrically. Recognising the first twelve square numbers and first five cube numbers by sight significantly speeds up students' work in later topics like factorising, simplifying surds, and estimating calculations.
Which year groups study square and cube numbers?
These worksheets cover Year 7 and Year 8 at KS3, when students formalise their understanding of indices and extend basic multiplication skills to powers. The National Curriculum introduces square numbers, cube numbers, and their corresponding roots during Year 7, expecting students to recall and use these values in calculations and problem-solving contexts. This groundwork becomes essential for manipulating expressions with indices in Year 8 and beyond.
Progression across these year groups typically moves from recognising and calculating squares and cubes to applying them in mixed problems involving prime factorisation, estimation, and reverse calculations. Year 7 students focus on fluency with values up to 12² and 5³, while Year 8 work incorporates these skills into multi-step problems, including finding square roots and cube roots, and using powers in real-world contexts. Teachers notice that regular retrieval practice with these values prevents students from relying on calculators for basic index calculations at GCSE.
How do square and cube numbers connect to geometry?
Square numbers directly represent the area of a square with integer side lengths—a square with sides of 7 cm has an area of 49 cm², demonstrating why 49 is called a square number. Similarly, cube numbers represent the volume of a cube: a cube with edges of 4 cm contains 64 cm³, making 64 a cube number. This geometric interpretation helps students visualise why these values grow so quickly and connects numerical work to spatial reasoning required in shape and measure topics.
These concepts appear throughout STEM applications, particularly in engineering and architecture where scaling matters. When dimensions double, area increases by a factor of four (the square) and volume by a factor of eight (the cube), explaining why larger vehicles need disproportionately more powerful engines or why small animals lose heat faster than large ones. Understanding squares and cubes numerically gives students the tools to tackle surface area to volume ratios in biology and scaling problems in physics and design technology.
How should teachers use these square and cube numbers worksheets?
The worksheets build from recognition and calculation exercises to problem-solving questions that require students to apply square and cube number knowledge in context. This structure allows teachers to assess whether students have moved beyond rote memorisation to genuine understanding of powers and roots. The answer sheets enable students to self-mark during independent work, turning worksheets into effective formative assessment tools where students identify their own misconceptions before moving on.
Many teachers use these resources for starter activities to maintain fluency with key values, as regular recall practice prevents students from forgetting squares and cubes between topics. They work well for intervention groups who missed this foundation in Year 7, for homework that consolidates classwork without requiring parental support, and for paired work where students explain their methods to each other. The PDF format means teachers can print specific sections for targeted practice rather than whole worksheets, adapting resources to individual student needs during revision or when addressing gaps identified through assessment.