Venn Diagrams Worksheets
What should students practise with venn diagrams worksheets?
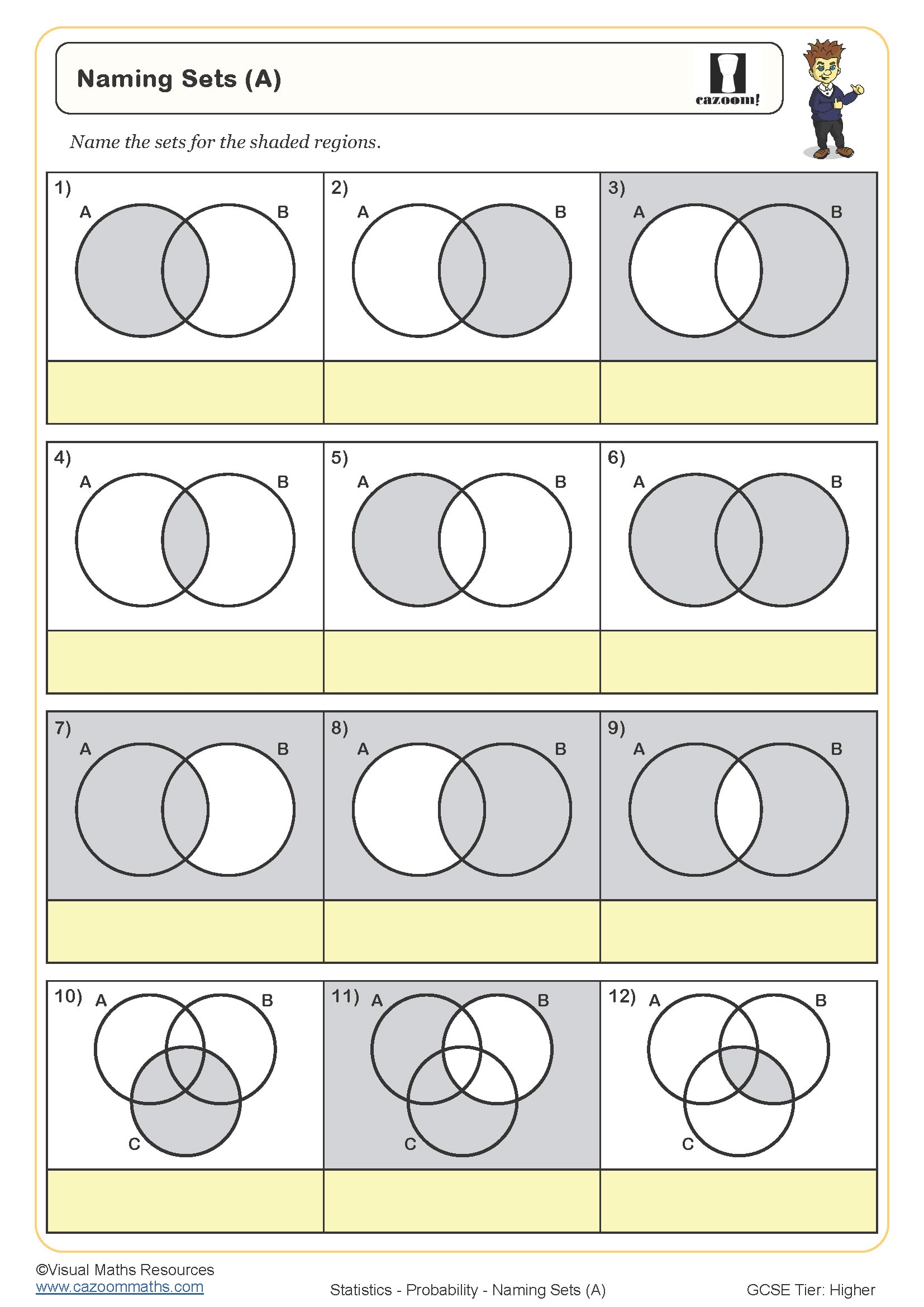
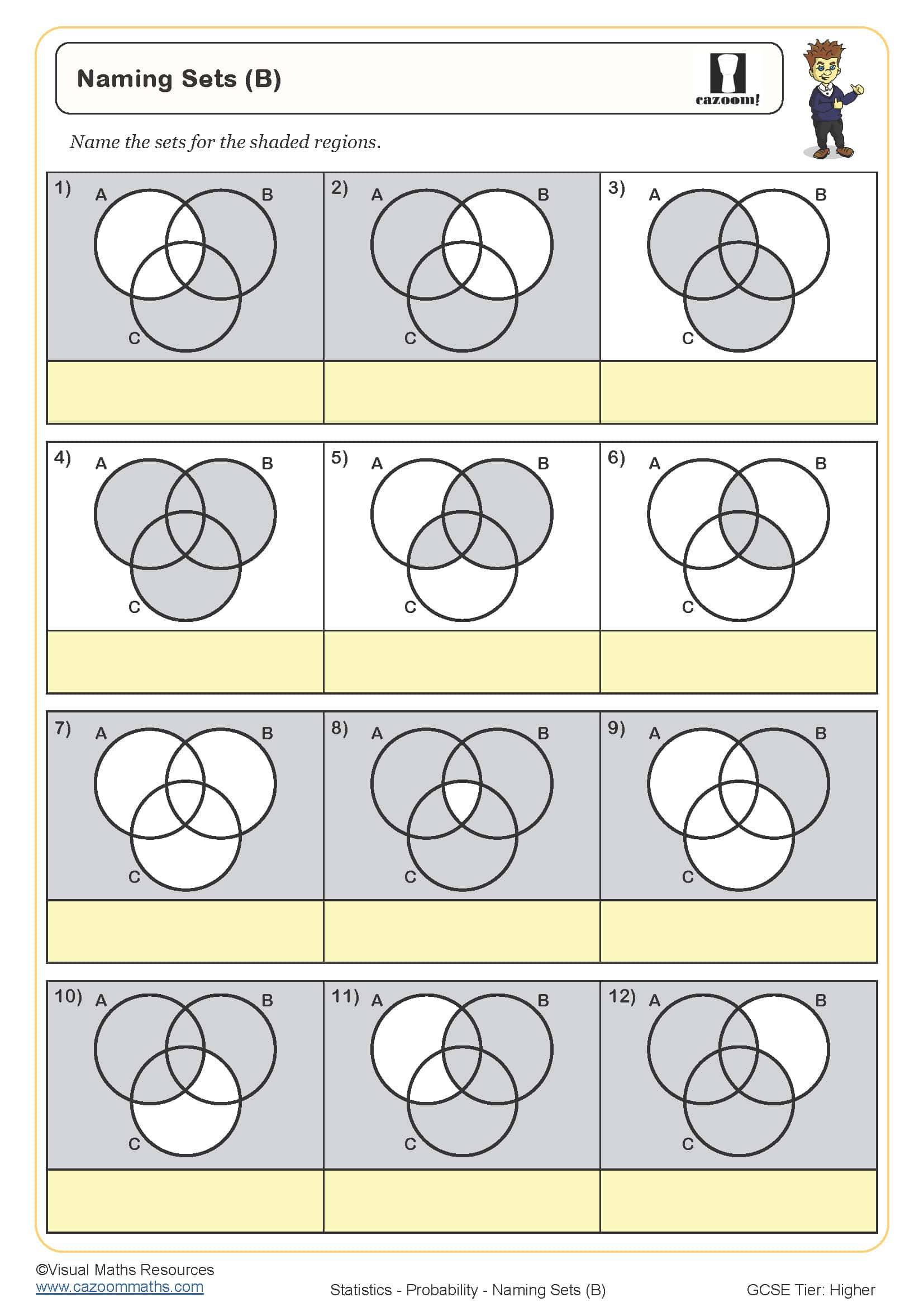
Venn diagrams worksheets should develop students' ability to represent data visually using overlapping circles, interpret the meaning of each region (including intersections and complements), and use the diagrams to solve problems involving sets, probabilities, and number properties. At KS3, this appears in the statistics strand, whilst at KS4 it extends into probability and problem-solving contexts where students must work with conditional probabilities or find missing values.
A common error occurs when students misinterpret what 'neither' means, placing values in the wrong region or forgetting to account for the universal set outside the circles. Students also frequently lose marks by calculating totals for individual sets without subtracting the intersection, leading to double-counting. Exam questions regularly test whether students can work backwards from incomplete diagrams, requiring algebraic thinking to establish unknown values before answering the actual question.
Which year groups use venn diagrams in maths?
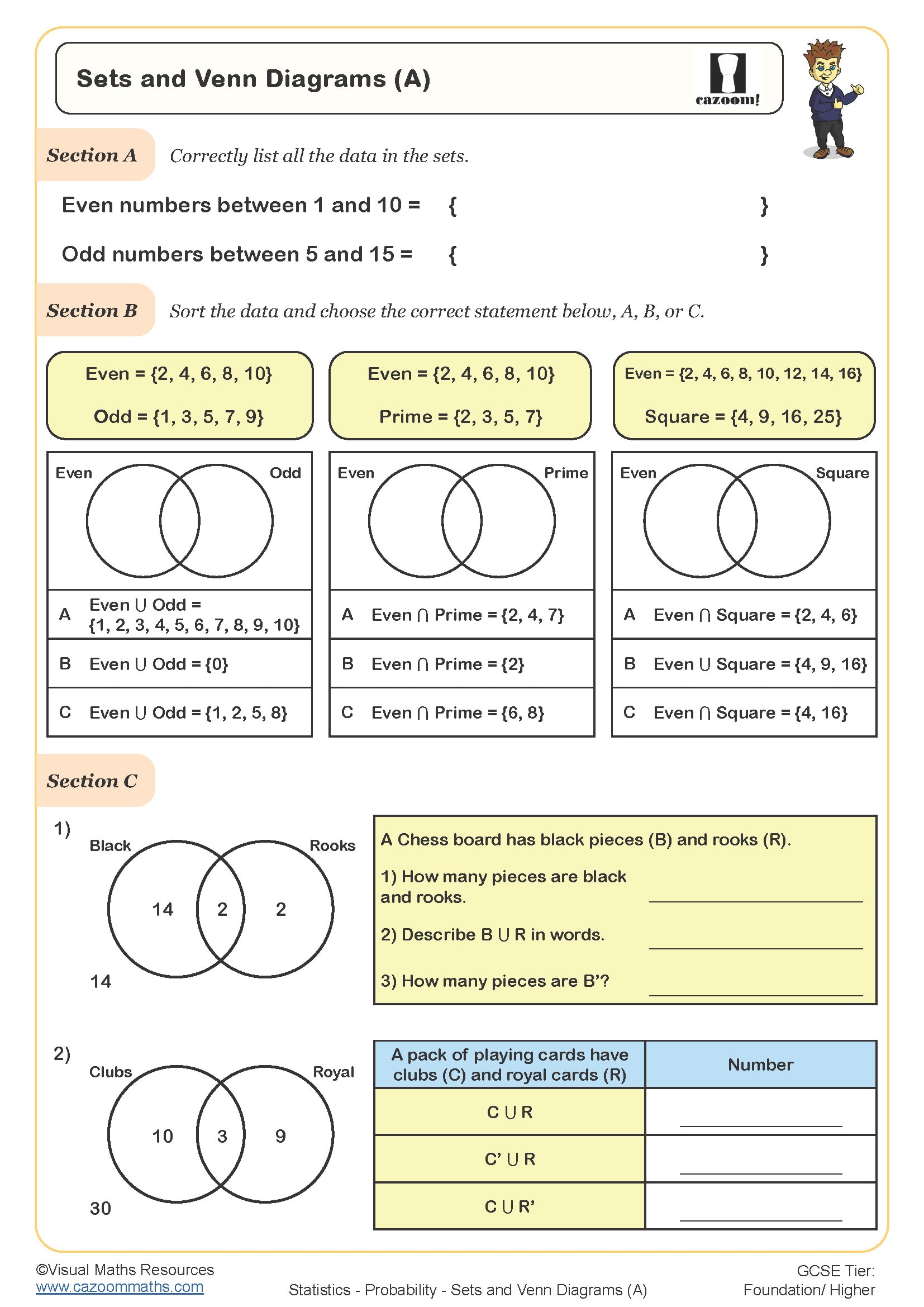
These worksheets cover Year 8, Year 9, and Year 10, spanning both Key Stage 3 and Key Stage 4. Students first encounter venn diagrams formally in Year 7 or 8 as part of the statistics curriculum, where they learn to sort data into categories and understand basic set notation. By Year 9, expectations include using venn diagrams to calculate probabilities and solve problems involving unions and intersections.
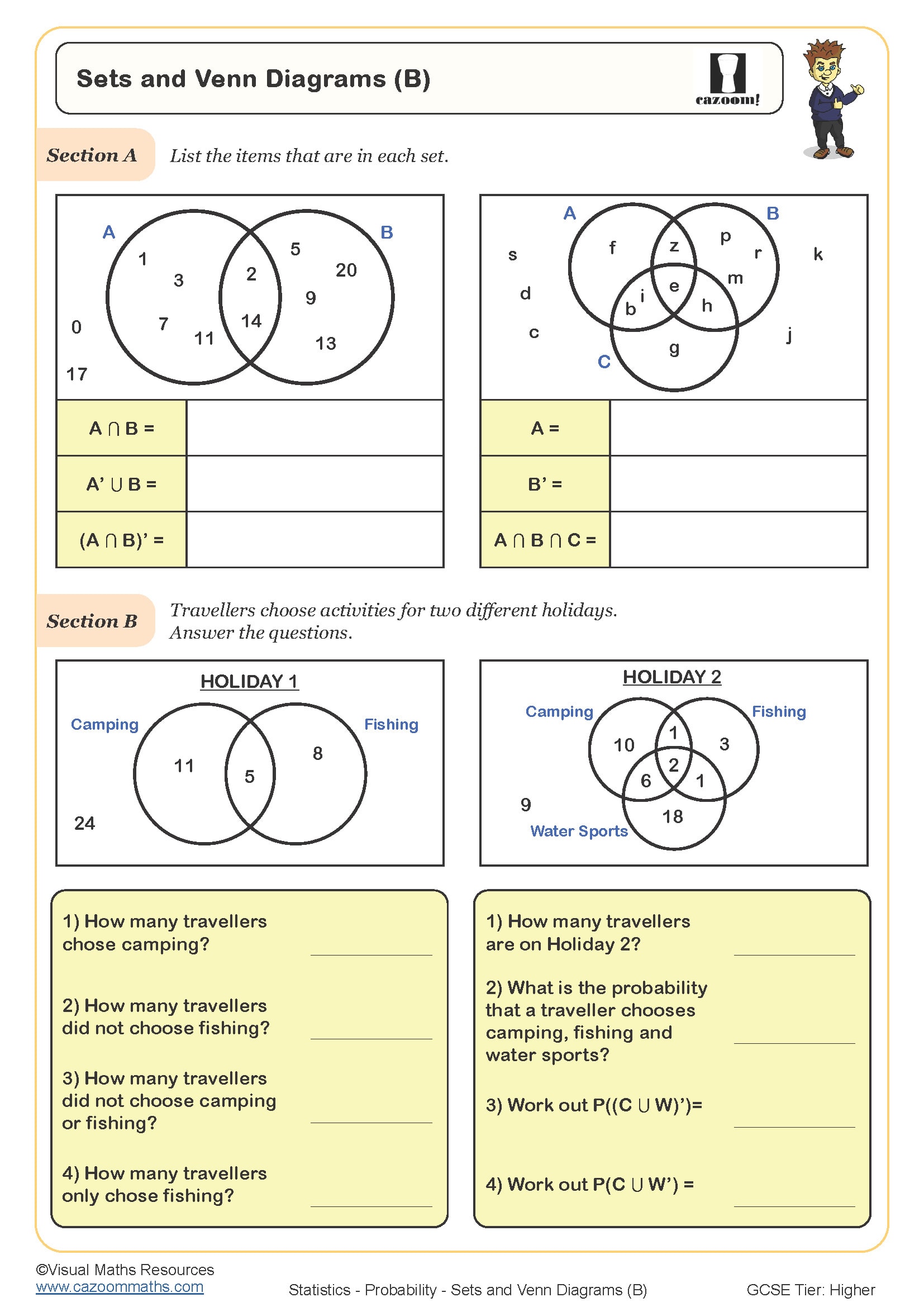
Progression continues into Year 10 where venn diagrams become tools for more sophisticated problem-solving, including finding HCF and LCM by sorting factors, solving conditional probability questions, and tackling algebraic problems where the number of elements in each region must be calculated first. Foundation tier GCSE questions typically involve two-set diagrams with straightforward calculations, whilst higher tier papers present three-set diagrams or require students to form and solve equations based on given constraints.
How do venn diagrams help find the lowest common multiple?
Using venn diagrams to find the lowest common multiple (LCM) involves sorting the prime factors of two or more numbers into regions showing which factors are unique to each number and which are shared. Students place shared prime factors in the intersection and unique factors in the separate regions, then multiply all factors that appear across the entire diagram to find the LCM. This visual method helps students understand why the LCM includes each prime factor at its highest power.
This approach connects directly to computer science and digital systems, where LCM calculations determine synchronisation points in repeating processes. For example, traffic light timing systems use LCM to calculate when signals will simultaneously show green, whilst task scheduling algorithms in operating systems rely on finding common multiples to coordinate processes. The venn diagram method makes these abstract calculations concrete, showing students exactly which factors contribute to the answer and why certain factors appear only once despite being in multiple numbers.
How do these venn diagram worksheets support classroom teaching?
The worksheets provide structured practice that builds from interpreting completed diagrams through to constructing and solving complex problems independently. Each sheet includes worked examples or scaffolded questions that demonstrate the step-by-step process of filling in regions systematically, starting with the intersection and working outwards. Answer sheets allow students to self-check their working, which is particularly valuable since venn diagram errors often compound, with one incorrect region affecting all subsequent calculations.
Teachers use these sheets for targeted intervention when students struggle with set notation or probability, as homework to consolidate lesson content, or as starter activities to reactivate prior knowledge before tackling exam-style questions. They work well for paired practice where students compare their region calculations and identify discrepancies, encouraging mathematical discussion about why certain values belong in specific regions. The progression across difficulty levels makes differentiation straightforward, allowing teachers to assign appropriate challenge while keeping the whole class working on the same fundamental concept.