Surds Worksheets

Our printable Surds Worksheets with answers are perfect to support your students in Year 9 to Year 11. They will be able to practise various surd operations on their own. These worksheets include exercises on simplifying surds, rationalising denominators, and performing arithmetic operations with surds. Each of these worksheet are specifically curated to help your students through these algebra concepts step by step. This way our surd resources are really helpful for your pupil to reinforce their understanding and problem-solving abilities. Suitable for both classroom use and independent study, these resources are a valuable addition to any GCSE algebra worksheet collection. Therefore, these questions are perfect for your students.

Add and Subtract Surds

Year groups: 10, 11

Rationalising Surds (D)

Year groups: 10, 11

Rationalising the Denominator - First Steps

Year groups: 10, 11

Rationalising the Denominator - with Binomial Denominators

Year groups: 10, 11

Rationalising the Denominator - with Binomial Numerators

Year groups: 10, 11

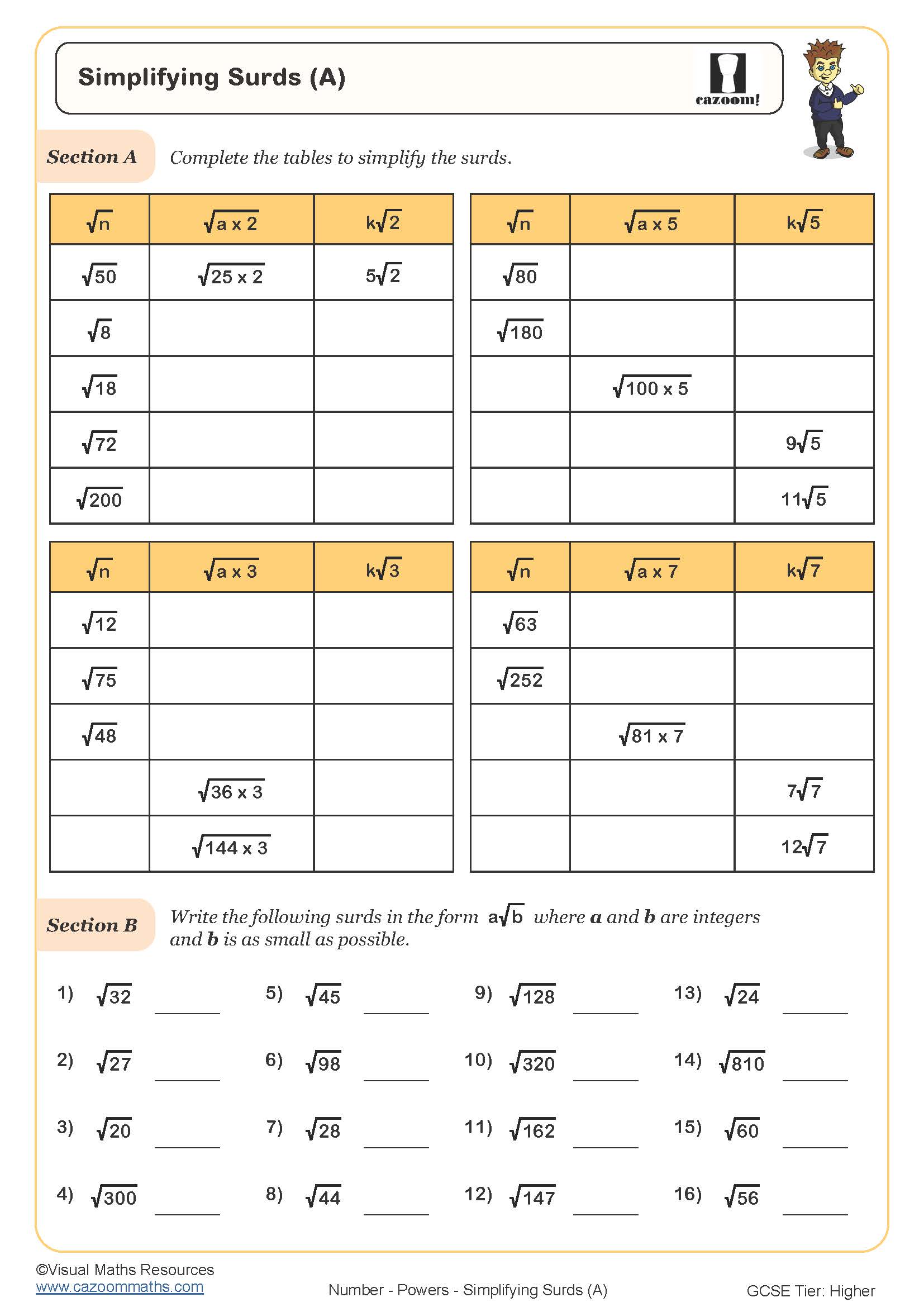
Simplifying Surds (A)

Year groups: 10, 11

Simplifying Surds (B)

Year groups: 10, 11

Simplifying Surds with Brackets (C)

Year groups: 10, 11

Writing Exact Answers Using Surds

Year groups: 10, 11

Printable Surds Worksheets with Answers

Download our printable PDF surds worksheets with separate answer sheets to support your students right away! These questions will help them in practising various surd operations, like—Add and Subtract Surds, Rationalising Surds, Simplifying Surds, Rationalising the Denominator and many more. Each of these worksheets is well-structured to guide your students through these core algebra concepts step by step. These worksheets are therefore suitable for both classroom use and independent study. These resources are proven to be a valuable addition to the GCSE algebra practice.

What Are Surds in Maths?

The basic idea of surds is irrational numbers that cannot be simplified to remove the square root (or cube root, etc.). Let’s take an example, √2 and √3 are surds because they cannot be expressed as exact decimals or fractions. Therefore, understanding this basic algebra concept is crucial for higher-level maths. Our surds worksheets are specially created by maths experts to provide comprehensive practice in identifying and working with surds, and using this concept while solving different maths problems.

Why Are Surds Important in GCSE Maths?

Surds are an important part of the GCSE maths curriculum, especially for higher-tier maths. Your children are expected to simplify surds, perform operations with them, and rationalise denominators in complex expressions in their KS3 and KS4 maths. By mastering this concept will therefore help your students in their algebra skills and is really important for solving advanced mathematical problems. Our GCSE surds worksheets offer targeted practice to help students develop skills like—Add and Subtract Surds, Rationalising Surds, Simplifying Surds, Rationalising the Denominator and many more.

Real-Life Applications of Surds

While surds are a mathematical concept, they have practical applications in various fields such as engineering, physics, and architecture, where precise calculations are necessary. For instance, surds are used in calculating exact lengths and areas that cannot be simplified into rational numbers. Understanding and working with surds enable students to apply mathematical principles to real-world problems. Our surds worksheets bridge the gap between theoretical knowledge and practical application, fostering a deeper appreciation of mathematics in everyday life.