Year 10 Surds Worksheets

These Year 10 surds worksheets provide focused practice on manipulating surds, from simplifying and performing operations to rationalising denominators and working with brackets. Surds appear frequently in GCSE higher tier papers, particularly in questions involving trigonometry, Pythagoras' theorem, and algebraic manipulation, so secure understanding at this stage directly impacts exam performance. Teachers often notice students struggle when rationalising denominators, especially identifying the correct conjugate to multiply by, or forgetting to simplify the surd fully after expanding brackets. Each worksheet includes complete answer sheets in PDF format, allowing students to check working independently and identify where errors occur. This collection builds the algebraic fluency needed for later topics including quadratic surds and exact trigonometric values.

Add and Subtract Surds

Expanding Double Brackets with Surds - Using the Grid Method

Pythagoras with Surds

Rationalising Surds (D)

Rationalising the Denominator - First Steps

Rationalising the Denominator - with Binomial Denominators

Rationalising the Denominator - with Binomial Numerators

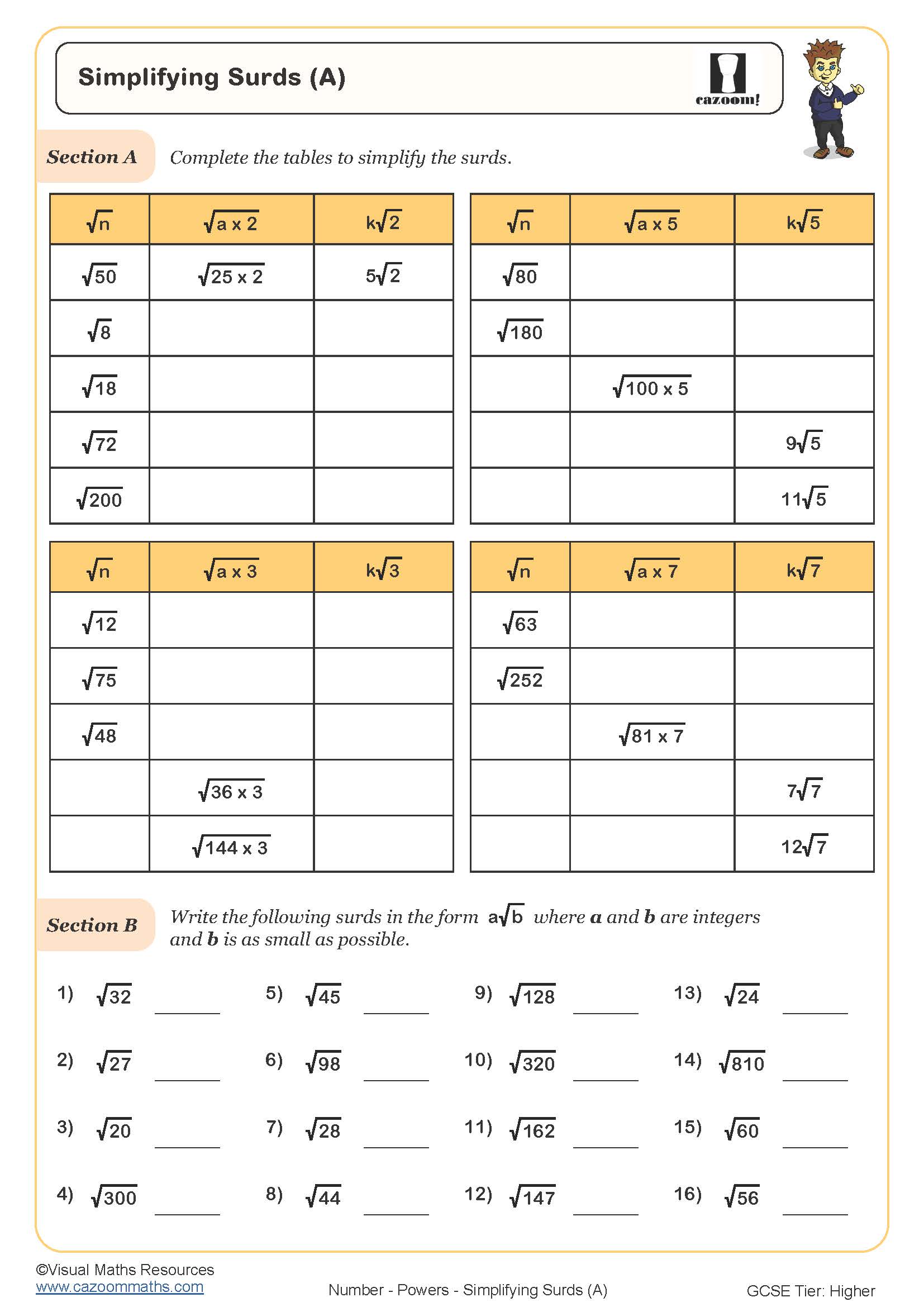
Simplifying Surds (A)

Simplifying Surds (B)

Simplifying Surds with Brackets (C)

Writing Exact Answers Using Surds

What should students learn from a surds Year 10 worksheet?

A year 10 surds worksheet should cover simplifying surds by identifying square factors, adding and subtracting like surds, multiplying and dividing surds, and rationalising denominators. Students also need practice expanding brackets involving surds and recognising when answers should remain in surd form rather than converting to decimals. This sits within the Number and Algebra strands of the KS4 National Curriculum and appears across multiple GCSE higher tier papers.

Teachers frequently observe students attempting to add unlike surds (treating √2 + √3 as √5) or losing marks by leaving √12 instead of simplifying to 2√3. Mark schemes consistently penalise unsimplified surds, even when the method is correct, so repeated practice identifying and extracting square factors becomes essential for securing marks in exam conditions.

Which year groups study surds?

Surds are introduced at KS4, typically in Year 10 for higher tier GCSE students. This topic requires secure understanding of square numbers, prime factorisation, and basic algebraic manipulation, which is why it appears after students have consolidated these foundational skills in Key Stage 3. Surds form part of the higher tier content and don't appear on foundation papers.

Within Year 10, the difficulty progresses from simplifying single surds like √50 to more complex manipulation involving brackets such as (√3 + 2)(√3 - 5), then advancing to rationalising denominators with expressions like 1/(√5 - 2). By the end of Year 10, students should handle multi-step problems combining several surd operations, preparing them for AS-level mathematics where surds appear in calculus and exponential functions.

How does rationalising denominators with surds work?

Rationalising the denominator means converting a fraction with a surd in the denominator to an equivalent form with a rational denominator. For simple cases like 1/√3, students multiply both numerator and denominator by √3 to get √3/3. For expressions with two terms like 1/(√5 + 2), they multiply by the conjugate (√5 - 2)/(√5 - 2), using the difference of two squares to eliminate the surd from the denominator, giving (√5 - 2)/1.

This technique proves valuable in physics and engineering contexts where exact values matter. Engineers calculating resonant frequencies or physicists working with quantum mechanics often express answers in surd form to maintain precision, since decimal approximations introduce rounding errors that compound through subsequent calculations. Understanding why √2/2 differs from 0.707 becomes important when designing circuits or calculating wavelengths where accuracy determines whether systems function correctly.

How do these worksheets support learning surds?

The worksheets scaffold learning by starting with straightforward simplification before progressing to operations and harder rationalising problems. Questions typically build from identifying square factors, through combining like surds, to multi-step problems requiring several operations. Answer sheets allow students to check each stage of working, helping them identify whether errors occur during simplification, multiplication, or rationalising steps, rather than just seeing a final answer marked wrong.

Teachers use these worksheets for intervention with students who struggle during initial teaching, as homework to consolidate classwork, or as targeted revision before assessments. They work well for paired activities where students compare methods for rationalising denominators or challenge each other to spot unsimplified surds. The clear progression across questions also suits independent study, allowing students to self-assess readiness before attempting exam-style questions that combine surds with other algebraic topics.